ClassBD Outperforms Competitors in Real-World Bearing Fault Diagnosis Using PU Dataset | HackerNoon

Table of Links

Abstract and 1. Introduction

2. Preliminaries and 2.1. Blind deconvolution

2.2. Quadratic neural networks

3. Methodology

3.1. Time domain quadratic convolutional filter

3.2. Superiority of cyclic features extraction by QCNN

3.3. Frequency domain linear filter with envelope spectrum objective function

3.4. Integral optimization with uncertainty-aware weighing scheme

4. Computational experiments

4.1. Experimental configurations

4.2. Case study 1: PU dataset

4.3. Case study 2: JNU dataset

4.4. Case study 3: HIT dataset

5. Computational experiments

5.1. Comparison of BD methods

5.2. Classification results on various noise conditions

5.3. Employing ClassBD to deep learning classifiers

5.4. Employing ClassBD to machine learning classifiers

5.5. Feature extraction ability of quadratic and conventional networks

5.6. Comparison of ClassBD filters

6. Conclusions

Appendix and References

4.2. Case study 1: PU dataset

4.2.1. Dataset description

The PU dataset was collected by Paderborn University (PU) Bearing Data Center [79]. This dataset encompasses multiple faults for 32 bearings, including vibration and current signals. The bearings were categorized into three groups: i) Six healthy bearings; ii) Twelve bearings with manually-induced damage (seven with outer race faults, five with inner race faults); iii) Fourteen bearings with real damage, induced by accelerated lifetime tests (five with outer race faults, six with inner race faults, and three with multiple faults). Four operating conditions were implemented, varying the rotational speed (N = 1500rpm or N = 900rpm), load torque (M = 0.7Nm or M = 0.1Nm), and radial force (F = 1000N or F = 400N). The sampling frequency was set at 64KHz. This dataset is one of the more difficult datasets in the field of bearing fault diagnosis [71].

In this study, we exclusively utilize the real damaged bearings for classification to validate the methods in real-world scenarios. We classify the fourteen faulty bearings and six healthy bearings into fourteen categories, as illustrated in Table 3. All the four operating conditions are tested in the experiments, with the codes assigned as N09M07F10, N15M01F10, N15M07F4, and N15M07F10.

Given the large volume of data in the PU dataset, each bearing has 20 segments, so we do not use overlapping to construct the datasets. We slice 20 × 2048 sub-segments with a stride of 2048, resulting in 400 data per bearing. The total number of datasets is 7600 × 2048. The data collected in the first 19 segments are randomly divided into training and validation sets at a ratio of 0.8:0.2, while the data from the 20th segment are allocated to the test set. Consequently, the dataset includes 5776 training data, 1444 validation data, and 380 test data. Lastly, we established four SNR levels (-4dB, -2dB, 0dB, 2dB) to evaluate the diagnosis performance.

4.2.2. Classification results

The classification results are presented in Table 4. We highlight key findings from the analysis. Notably, the ClassBD model demonstrates superior performance compared to its competitors across various noise levels and operating conditions. Overall, the average F1 scores of ClassBD on the four conditions are higher than 94%. Specifically, under high noise conditions (at -4 dB), the ClassBD exhibits a substantial performance gap relative to other methods. For instance, on the N15M01F10 dataset with -4dB noise, the ClassBD achieves an impressive 95% F1 score, while the second-best method, EWSNet, only attains 70% F1. These results underscore the efficacy of ClassBD as a robust anti-noise model, consistently delivering competitive performance across diverse high-noise scenarios.

4.2.3. Classification under small sample conditions

In this study, we rigorously assess the performance of various methods under the challenging scenario of extremely limited sample availability. While our approach is not explicitly tailored for small sample issues, we conduct straightforward tests to gain insights into their behavior.

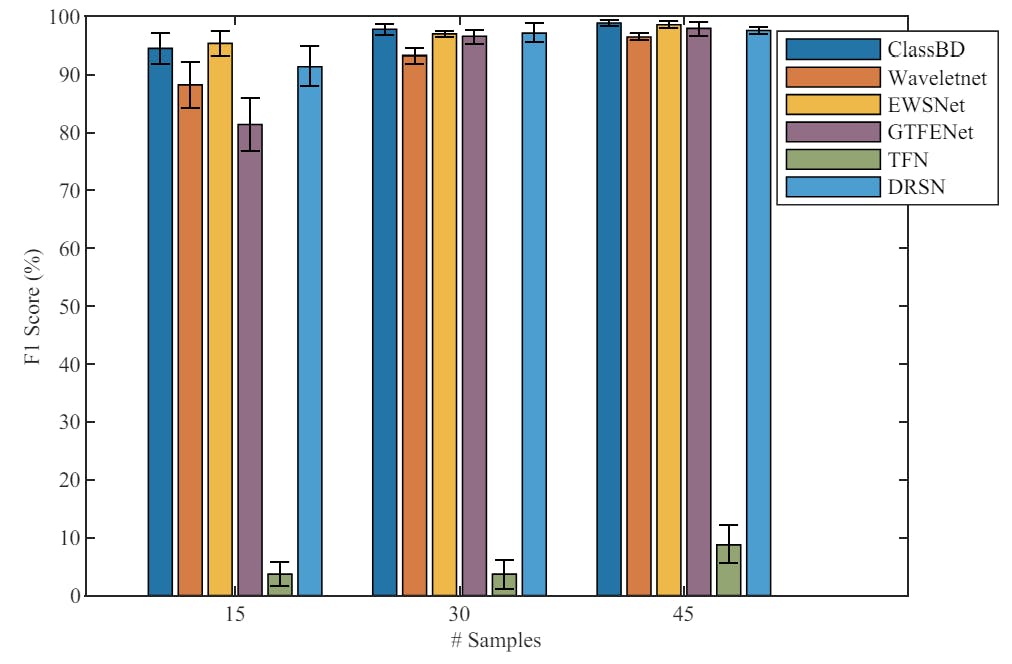
Specifically, we employ the N09M07F10 dataset, comprising 20 signal segments per category. In the most stringent case, we retain only one sample from each signal segment, reserving the last segment of the signal as the test set. Consequently, we collect one to three samples from each signal segment and finally compose 15, 30, and 45 samples per class for training sets. Notably, we exclude noise from this experiment.

The results, depicted in Figure 3, reveal that even under these constrained conditions, the ClassBD, EWSNet, and DRSN models exhibit commendable performance. Remarkably, all three methods achieve over 90% F1 scores with a training dataset of just 15 samples per class. Notably, the performance of ClassBD and EWSNet closely align. Their average F1 scores stand at 97.70% and 97.47%, respectively, positioning them as the top-performing approaches. In summary, our findings underscore the promising potential of ClassBD in addressing the challenges posed by small sample sizes