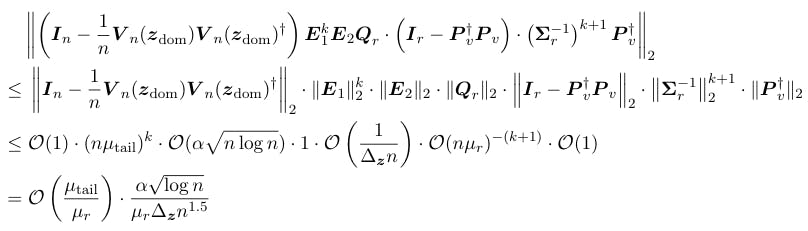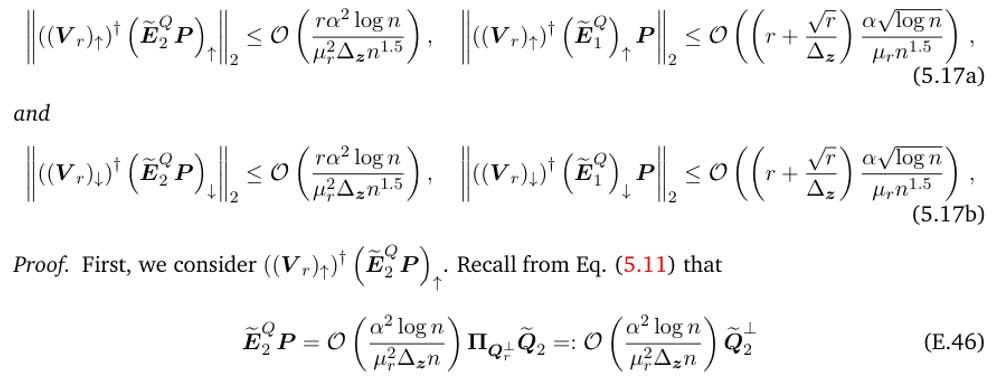Eigenvector Perturbation in Aligning Matrix Construction for ESPRIT | HackerNoon

Table of Links

Abstract and 1 Introduction

1.1 ESPRIT algorithm and central limit error scaling

1.2 Contribution

1.3 Related work

1.4 Technical overview and 1.5 Organization

2 Proof of the central limit error scaling

3 Proof of the optimal error scaling

4 Second-order eigenvector perturbation theory

5 Strong eigenvector comparison

5.1 Construction of the “good” P

5.2 Taylor expansion with respect to the error terms

5.3 Error cancellation in the Taylor expansion

5.4 Proof of Theorem 5.1

A Preliminaries

B Vandermonde matrice

C Deferred proofs for Section 2

D Deferred proofs for Section 4

E Deferred proofs for Section 5

F Lower bound for spectral estimation

References

E Deferred proofs for Section 5

E.1 Proof for Step 1: Construction of the “good” P

which gives the expression of P Eq. (5.2) in the lemma.

Property I and II follow from Claim E.2. The proof of the lemma is then complete

E.1.1 Technical claims

Proof. Note that

For the first term, we have

For the second term, we have

Combining them together, we have

The claim is then proceed.

Claim E.2 (Properties of the “good” P). The invertible matrix P defined by Eq. (5.2) satisfies the following properties:

Proof. We prove each of the properties below.

Proof of Property I:

By the definition of P (Eq. (5.2)), we have

Proof of Property II:

Consider

E.2 Proofs for Step 2: Taylor expansion with respect to the error terms

Lemma 5.3. Let P be defined as Eq. (5.2). Then, we have

By Claim E.4, the Neumann series in Eq. (E.10) can be truncated up to second order:

And for the residual term, we have

Finally, combining Eqs. (E.11) to (E.14) together, we obtain that

where we re-group the terms in the second step.

The proof of the lemma is completed.

Lemma 5.4. It holds that

Proof. We first deal with the first order term in Eq. (5.8):

To bound (I), we notice

Combining this and Eq. (5.4), we obtain

Next, we keep (II) and first consider the second-order term in Eq. (5.8), which can be rewritten as follows:

where the first two steps follow from re-grouping the terms, and the last step follows from Eq. (E.22) and Eq. (E.17).

Plugging the bounds for the first order and the second order terms into Eq. (5.8), we get that

which proves the lemma.

E.2.1 Technical claims

where the first step follows from Eq. (1.13) that

the second step follows from triangle inequality, and the third step follows from Lemma 1.7 and Corollary B.2.

This implies that

Claim E.4 (Neumann series truncation). It holds that

Proof. For the Neumann series term in Eq. (E.10):

we first bound the middle bracket:

The first-order term (i.e., k = 1) in Eq. (E.21) can be approximated as follows:

where the first step follows from triangle inequality, the second step follows from Eq. (E.18) and Eq. (E.22), and the last step is by direct calculation.

By a similar calculation, we can show that the second-order term (i.e., k = 2) in Eq. (E.21) can be approximated by

Indeed, this term can be further simplified:

where the first step follows from triangle inequality, the second step follows from Eq. (E.18) and Eq. (E.22), and the last step follows from the geometric summation.

Combining Eq. (E.23) to Eq. (E.26) together, we get that

The claim is then proved.

E.3 Proofs for Step 3: Error cancellation in the Taylor expansion

E.3.1 Establishing the first equation in Eq. (5.10)

Proof. In this proof, we often use the following observations:

They are proved in Claim E.5.

we have

where the third step uses Lemma 1.7 for the first term, Eq. (C.1) for the second term, Lemma C.1 for the third term, Eq. (1.14) for the fifth and seventh terms, Eq. (B.2) for the sixth term. Thus,

To bound the second term in the above equation, for any k ≥ 0, we have

Therefore, we obtain that

Similarly, we also have

Plugging Eq. (E.30) into Eq. (E.28) and Eq. (E.29), we have

The proof of the lemma is completed.

Lemma 5.6.

Proof. We analyze Eq. (5.13b) and Eq. (5.13c) column-by-column.

Combining the above two equations together and summing over k, we obtain that

By Eq. (5.13b) and Eq. (5.13c), we have

Without loss of generality, we only consider the first column of Eq. (E.33):

where the second step follows from the Toeplize structure of the matrix. Therefore, by triangle inequality,

where the second step follows from Eq. (E.35)-Eq. (E.37).

Now, we consider the first term of F1. Define

where the second step follows from Eq. (E.39). The above two equations imply that

Plugging in the values of k = 0 in Eq. (E.35) and Eq. (E.36), we obtain for any k > 0

which implies that

Thus, we obtain that

Combining Eq. (E.44) and Eq. (E.45) together, the lemma is proved.

Lemma 5.9.

Then, we bound Eq. (E.50) and Eq. (E.51) separately.

For Eq. (E.50), we have

For Eq. (E.51), we notice that

Hence, combining Eq. (E.52) and Eq. (E.53) together, we obtain

Therefore, we complete the proof of the lemma.

E.3.3 Technical claims

Thus, LHS of Eq. (E.55) can be expressed as:

By a slightly modified proof of Corollary B.2, it is easy to show that

Together with Lemma 1.7, we obtain that

which proves the first part of the claim.

Next, we prove Eq. (E.55b).

When k = 0, Eq. (E.55b) becomes

which follows from Lemma 1.7.

When k ≥ 1, we have

Similarly, the second term can be bounded by:

The third term can be bounded by:

Hence, to prove Eq. (E.55b), it suffices to bound

where the first step follows from Lemma 1.7, and the second step follows from Eq. (1.14). Combining the above three equations together, we obtain

where the second step follows from using Corollary B.3. This proves the k = 1 case of Eq. (E.55b).

Finally, by induction Eqs. (E.56) to (E.59), we can prove that for any k ≥ 2,

This concludes the proof of Eq. (E.55b).

Claim E.6.

The claim then follows.