New Research Shows Classic Selfish Mining Is Outdated | HackerNoon

Table of Links

Abstract and 1. Introduction

1.1 Related Work

2. Preliminaries

   2.1 System Model

   2.2 Selfish Mining Objective

   2.3 Markov Decision Processes

3. Selfish Mining Attack

   3.1 Overview

   3.2 Formal Model

   3.3 Formal Analysis

   3.4 Key Features and Limitations

4. Experimental Evaluation

5. Conclusion, Acknowledgments, and References

A. NAS Mining Objectives

B. Efficient Proof Systems

C. Proof of Theorem 3.1

4 EXPERIMENTAL EVALUATION

We implement the MDP model and the formal analysis procedure presented in Section 3 and perform an experimental evaluation towards answering the following research questions (RQs):

RQ1 What is the expected relative revenue that our selfish mining strategy achieves? How does it compare to direct extensions of classic selfish mining attacks on PoW blockchains [11] or to mining honestly?

RQ2 How do different values of the System Model parameters impact the expected relative revenue that our selfish mining attack can achieve? The System Model parameters include the relative resource of the adversary 𝑝 ∈ [0, 1] and the switching probability 𝛾 ∈ [0, 1].

Baselines. To answer these RQs, we compare our selfish mining attack against two baselines:

(1) Honest mining strategy. This is the strategy extending only the leading block of the main chain.

(2) Single-tree selfish mining attack. This is the attack strategy that exactly follows the classic selfish mining attack in Bitcoin proposed in [11], however it grows a private tree fork rather than a private chain. Analogously as in [11], the adversary publishes the private tree whenever the length of the main chain catches up with the depth of the private tree. We omit the formal model of this baseline due to space limitations. We also use this baseline to empirically evaluate how severe is the second limitation discussed in Section 3.4.

Experimental setup. We perform an experimental comparison of our attack and the two baselines for the values of the adversarial relative resource 𝑝 ∈ [0, 0.3] (in increments of 0.01) and the switching probability 𝛾 ∈ {0, 0.25, 0.5, 0.75, 1}. As for the parameters of each selfish mining attack:

• For our selfish mining attack, we set the maximal length of private forks 𝑙 = 4 and consider all combinations (𝑑, 𝑓 ) ∈ {(1, 1), (2, 1), (2, 2), (3, 2), (4, 2)} of the values of the attack depth 𝑑 and the forking number 𝑓 .

• For the single-tree selfish mining attack baseline, we set the maximal depth of the private tree 𝑙 = 4 to match our maximal private fork length, and the maximal width of the private tree 𝑓 = 5.

All experiments were run on Ubuntu 20, 2.80GHz 11th Gen Intel(R) Core(TM) i7-1165G7 CPU, 16 GB RAM, and 16 GB SWAP SSD Memory. For solving mean-payoff MDPs, we use the probabilistic model checker Storm [18], a popular MDP analysis tool within the formal methods community[2].

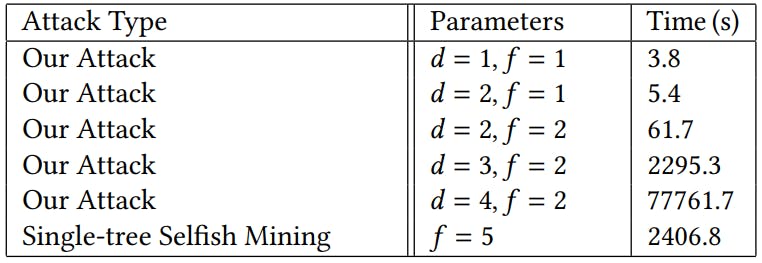
Results. Table 1 shows the runtimes of both our selfish mining attack as well as the single-tree selfish mining attack given various parameter settings and for a fixed switching parameter of 𝛾 = 0.5. We only show timings for 𝛾 = 0.5 as we found the runtimes of our experiments to be very similar across all 𝛾 parameter settings. As can be seen from Table 1, increasing the depth of the attack increases the runtime of our evaluation by an order of magnitude due to the exponential increase in state space.

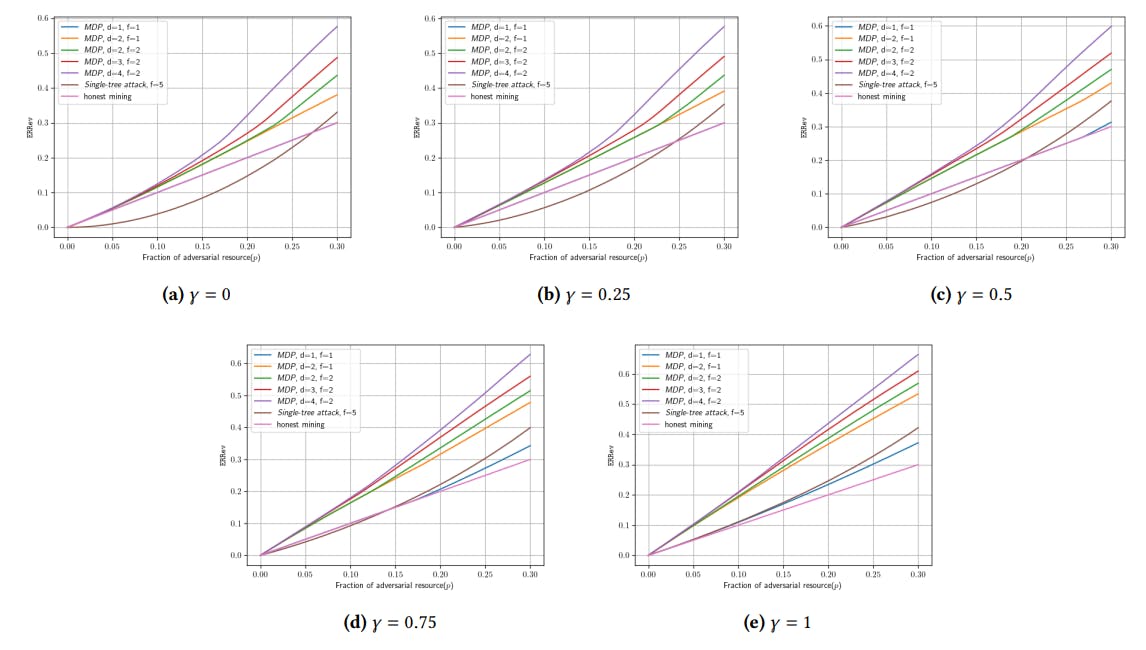
Experimental results are shown in Figure 2, showing plots for each 𝛾 ∈ {0, 0.25, 0.5, 0.75, 1}. As we can see from the plots, our selfish mining attack consistently achieves higher expected relative revenue ERRev than both baselines for each value of 𝛾, except when 𝑑 = 1 and 𝑓 = 1. Indeed, already for 𝑑 = 2 and 𝑓 = 1 when the adversary grows a single private fork on the first two blocks in the main chain, our attack achieves higher ERRev than both baselines. This shows that growing private forks at two different blocks already provides a more powerful attack than growing a much larger private tree at a single block. Hence, our results indicate that growing disjoint private forks rather than trees is not a significant limitation, justifying our choice to grow private forks towards making the analysis computationally tractable.

The attained ERRev grows significantly as we increase 𝑑 and 𝑓 and allow the adversary to grow more private forks. In particular, for 𝑑 = 4, 𝑓 = 2, and relative adversarial resource 𝑝 = 0.3, our attack achieves ERRev that is larger by at least 0.2 than that of both baselines, for all values of the switching probability𝛾. This indicates a significant advantage of selfish mining attacks in efficient proof systems blockchains compared to PoW, as the ability to simultaneously grow multiple private forks on multiple blocks translates to a much larger ERRev. Our results suggest that further study of techniques to reduce the advantage of the adversary when mining on several blocks is important in order to maintain reasonable chain quality for efficient proof systems blockchains.

Finally, we notice that larger 𝛾 values correspond to larger ERRev in our strategies. This is expected, as larger 𝛾 values introduce bias in the likelihood of the adversarial chain becoming the main chain. This is most pertinently observed in the case of 𝑑 = 𝑓 = 1: since 𝑑 = 𝑓 = 1 corresponds to a strategy that only mines a private block on the leading block in the main chain, the only way to deviate from honest mining is to withhold a freshly mined block and reveal it together with the occurrence of a freshly mined honest block. As we can see in the plots, for 𝛾 < 0.5 the achieved ERRev of the strategy with 𝑑 = 𝑓 = 1 corresponds to that of honest mining and the two lines in plots mostly overlap, whereas this strategy only starts to pay off for 𝛾 > 0.5 and for the proportion of resource 𝑝 > 0.25. Altogether, this suggests that further and careful analysis of the control of the adversary over the broadcast network as well as the fork choice breaking rule is necessary.

Key takeaways. The key takeaways of our experimental evaluation are as follows:

• Our selfish mining attack achieves significantly higher ERRev than both baselines, reaching up to 0.2 difference in ERRev. Thus, our results strongly suggest that growing private forks at multiple blocks is much more advantageous than growing all forks on the first block in the main chain.

• Our results suggest that growing private trees rather than disjoint private forks would not lead to a significant improvement in the adversary’s ERRev. Hence, the second limitation of our attack discussed in Section 3.4 does not seem to be significant.

• Our results suggest that enhancing security against selfish mining attacks in efficient proof system blockchains requires further and careful analysis of the control that the adversary has over the broadcast system. In particular, for large values of the switching probability 𝛾, even the simplest variant of our attack with 𝑑 = 1 and 𝑓 = 1 starts to pay off when 𝑝 > 0.25.

[2] Refer to our github repository for our implementation details: https://github.com/mehrdad76/Automated-Selfish-Mining-Analysis-in-EPSBlockchains