Neural Networks vs. Scalar Shock Waves | HackerNoon

Table of Links

Abstract and 1. Introduction

1.1. Introductory remarks

1.2. Basics of neural networks

1.3. About the entropy of direct PINN methods

1.4. Organization of the paper

2. Non-diffusive neural network solver for one dimensional scalar HCLs

   2.1. One shock wave

   2.2. Arbitrary number of shock waves

   2.3. Shock wave generation

   2.4. Shock wave interaction

   2.5. Non-diffusive neural network solver for one dimensional systems of CLs

   2.6. Efficient initial wave decomposition

3. Gradient descent algorithm and efficient implementation

   3.1. Classical gradient descent algorithm for HCLs

   3.2. Gradient descent and domain decomposition methods

4. Numerics

   4.1. Practical implementations

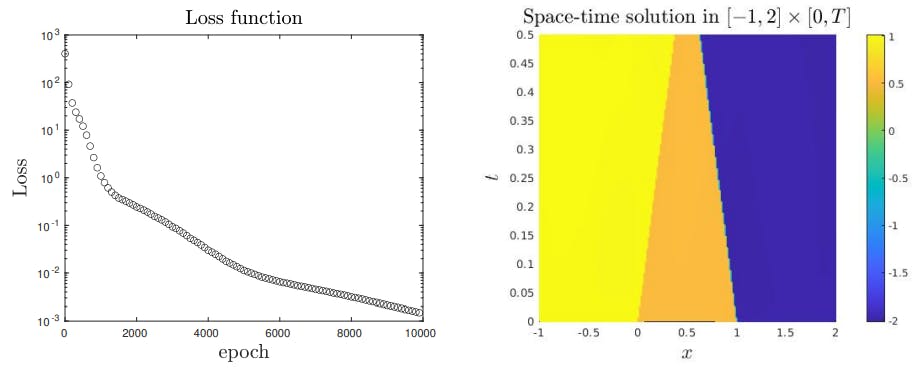
   4.2. Basic tests and convergence for 1 and 2 shock wave problems

   4.3. Shock wave generation

   4.4. Shock-Shock interaction

   4.5. Entropy solution

   4.6. Domain decomposition

   4.7. Nonlinear systems

5. Conclusion and References

2. Non-diffusive neural network solver for one dimensional scalar HCLs

In this section, we derive a NDNN algorithm for solving solutions to HCL containing (an arbitrary number of) shock waves. The derivation is proposed in several steps:

• Case of one shock wave.

• Case of an arbitrary number of shock waves.

• Generation of shock waves.

• Shock-shock interaction.

• Extension to systems.

Generally speaking for D shock waves, the basic approach will require 2D+1 neural networks, more specifically, D + 1 two-dimensional neural networks for approximating the local HCL smooth solutions, and D one-dimensional networks for approximating the DLs.

2.1. One shock wave

We consider (1) with boundary conditions when necessary (incoming characteristics at the boundary), with Ω = (a, b), and (without restriction) 0 ∈ Ω. We assume that the corresponding solution contains an entropic shock wave, with discontinuity line (DL) initially located at x = 0, parameterized by γ : t 7→ γ(t), with t ∈ [0, T] and γ(0) = 0. The DL γ separates Ω in two subdomains Ω−, Ω+ (counted from left to right) and Q in two time-dependent subdomains denoted Q− and Q+ (counted from left to right). We denote by u ± the solution u of (1) in Q±. Then (1) is written in the form of a system of two HCLs

which are coupled through the Rankine-Hugoniot (RH) condition along the DL for t ∈ [0, T],

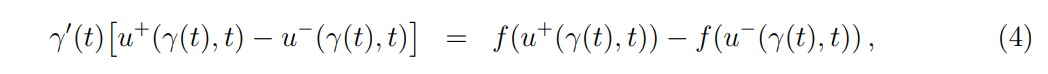
with the Lax shock condition reading as

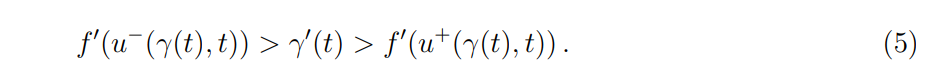
The proposed approach consists in approximating the DL and the solutions in each subdomain Q± with neural networks. We denote by n(t) the neural network approximating γ, with parameters θ and n(0) = 0. We will refer still by n to DL given by the image of n. Like in the continuous case, n separates Q in two domains, which are denoted again by Q±.

2.2. Arbitrary number of shock waves

This approach involves 2D+1 neural networks. Hence the convergence of the optimization algorithm may be hard to achieve for large D. However, the solutions ui being smooth and DLs being dimensional functions, the networks Ni and ni do not need to be deep.

:::info
Authors:

(1) Emmanuel LORIN, School of Mathematics and Statistics, Carleton University, Ottawa, Canada, K1S 5B6 and Centre de Recherches Mathematiques, Universit´e de Montr´eal, Montreal, Canada, H3T 1J4 ([email protected]);

(2) Arian NOVRUZI, a Corresponding Author from Department of Mathematics and Statistics, University of Ottawa, Ottawa, ON K1N 6N5, Canada ([email protected]).

:::

:::info
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.

:::