he Extinction Equation: What Happens When Advection Goes Too Far? | HackerNoon

Table of Links

Abstract and 1. Introduction

2. The well-posed global solution

3. Nontrivial stationary solution

   3.1 Spectral theory of integro-differential operator

   3.2 The existence, uniqueness and stability of nontrivial stationary solution

4. The sharp criteria for persistence or extinction

5. The limiting behaviors of solutions with respect to advection

6. Numerical simulations

7. Discussion, Statements and Declarations, Acknowledgement, and References

7 Discussion

The paper introduces a nonlocal reaction-diffusion-advection problem in a bounded region with Dirichlet/Neumann boundary condition. Our objective is to investigate its spatial dynamics, namely, the sharp criteria for persistence or extinction and the limiting behaviors of solutions with respect to advection rate. The main conclusions can be summarized as follows:

(1) The existence/nonexistence, uniqueness and stability of nontrivial stationary solutions are obtained. To be specific:

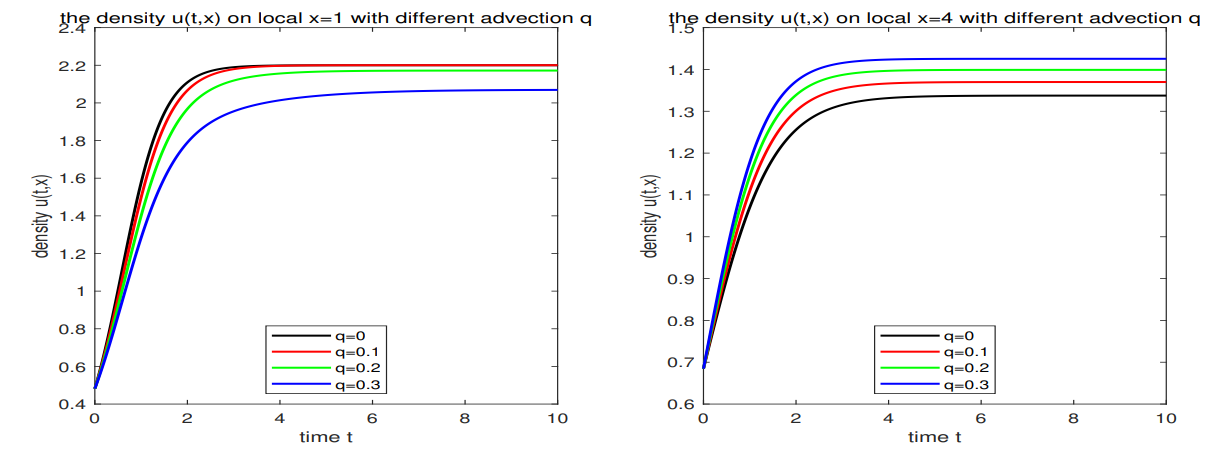
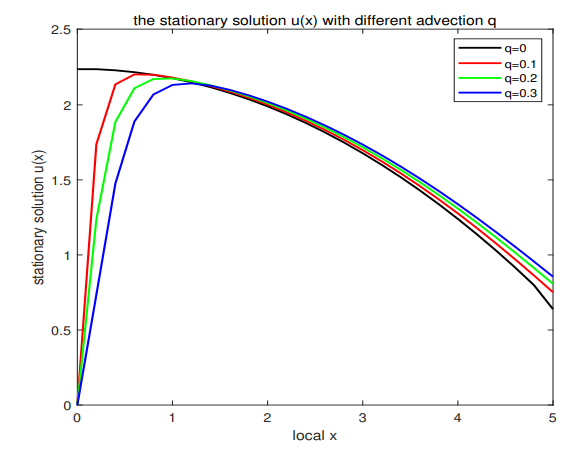
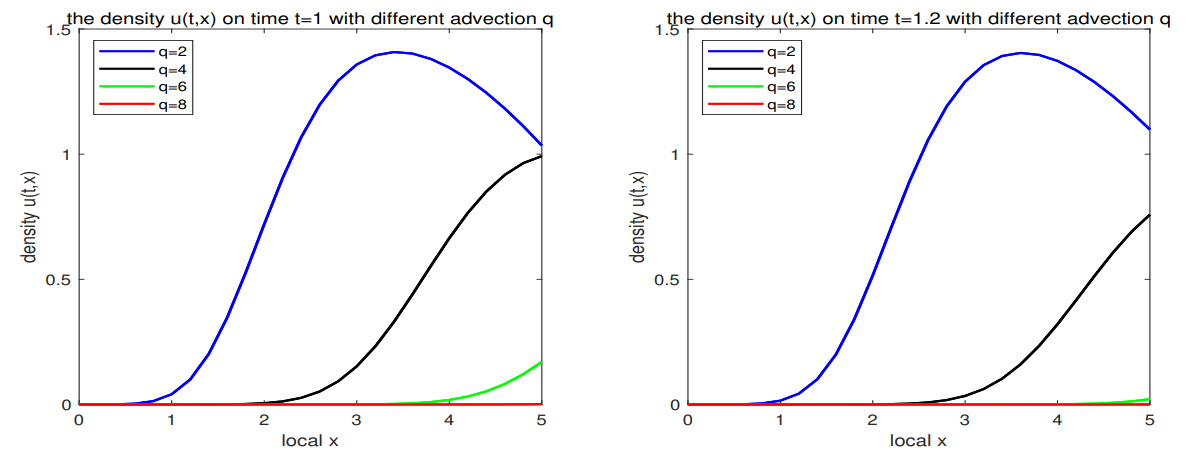
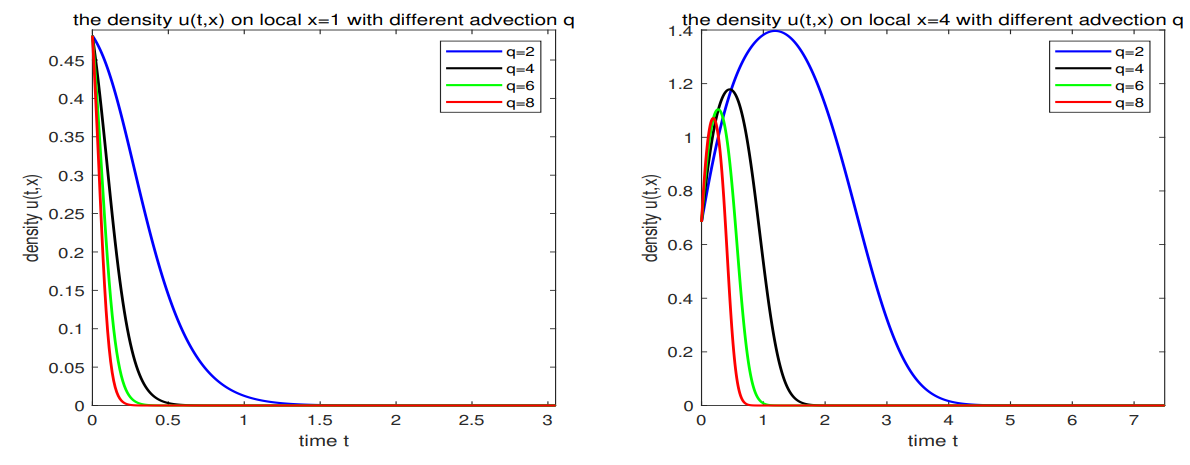
(3) The limiting behaviors of solutions with respect to advection rate are considered. It tells us that a sufficiently large directional motion will cause the species extinction in any situations.

(4) The numerical simulations verify our theoretical proof and show that the advection rate has a great impact on the dynamic behaviors of species.

Statements and Declarations

Competing Interests We declare that the authors have no competing interests as defined by Springer, or other interests that might be perceived to influence the results and/or discussion reported in this paper.

Acknowledgement

This work is supported in part by the National Natural Science Foundation of China (No. 11871475, 12271525) and the Fundamental Research Funds for the Central Universities of Central South University (No. CX20230218).

References

[1] Murray, J. D. 1989, Mathematical Biology, Springer Verlag, New York.

[2] Fisher, R. 1937, The wave of advance of advantageous genes, Ann. Eugen. London 7: 355-369.

[3] Skellam, J. G. 1951, Random dispersal in theoretical populations, Biometrica 38: 196-218.

[4] Hutson V, Martinez S, Mischaikow K, et al. The evolution of dispersal, J. Math. Biol., 2003, 47(6): 483-517.

[5] Crow J F. An introduction to population genetics theory, Scientific Publishers, 2017.

[6] Othmer H G, Dunbar S R, Alt W. Models of dispersal in biological systems, J. Math.Biol., 1988, 26(3): 263-298.

[7] Cortazar C, Coville J, Elgueta M, et al. A nonlocal inhomogeneous dispersal process, J. Differ. Equ., 2007, 241(2): 332-358.

[8] Cortazar C, Elgueta M, Rossi J D. Nonlocal diffusion problems that approximate the heat equation with Dirichlet boundary conditions, Israel J. Math., 2009, 170: 53-60.

[9] Andreu-Vaillo F, Mazon J M, Rossi J D, et al. Nonlocal diffusion problems, American Mathematical Soc., 2010.

[10] Cortazar C, Elgueta M, Rossi J D, et al. Boundary fluxes for nonlocal diffusion, J. Differ. Equ., 2007, 234(2): 360-390.

[11] Cortazar C, Elgueta M, Rossi J D, et al. How to approximate the heat equation with Neumann boundary conditions by nonlocal diffusion problems, Arch. Ration. Mech. Anal., 2008, 187: 137- 156.

[12] Coville J, Dupaigne L. Propagation speed of travelling fronts in nonlocal reaction-diffusion equations, Nonlinear Anal., 2005, 60(5): 797-819.

[13] Pan S, Li W, Lin G. Travelling wave fronts in nonlocal delayed reaction-diffusion systems and applications, Z. Angew. Math. Phys., 2009, 60(3): 377-392.

[14] Coville J, Davila J, Martinez S. Pulsating fronts for nonlocal dispersion and KPP nonlinearity, Ann. Inst. H.Poincare Anal. Non Lineaire, 2013, 30(2): 179-223.

[15] Li W, Sun Y, Wang Z. Entire solutions in the Fisher-KPP equation with nonlocal dispersal, Nonlinear Anal., 2010, 11(4): 2302-2313.

[16] Li W, Zhang L, Zhang G. Invasion entire solutions in a competition system with nonlocal dispersal, Discrete Contin. Dyn. Syst, 2015, 35(4): 1531-1560.

[17] Sun Y, Li W, Wang Z. Entire solutions in nonlocal dispersal equations with bistable nonlinearity, J. Diff. Equ., 2011, 251(3): 551-581.

[18] Bates P, Zhao G. Existence, uniqueness and stability of the stationary solution to a nonlocal evolution equation arising in population dispersal, J. Math. Anal. Appl., 2007, 332(1): 428-440.

[19] Kao C, Lou Y, Shen W. Random dispersal vs. non-local dispersal, Discrete Contin. Dyn. Syst, 2010, 26(2): 551-596.

[20] Coville J. On a simple criterion for the existence of a principal eigenfunction of some nonlocal operators, J. Diff. Equ., 2010, 249(11): 2921-2953.

[21] Garcia-Melian J, Rossi J D. On the principal eigenvalue of some nonlocal diffusion problems, J. Diff. Equ., 2009, 246(1): 21-38.

[22] Chasseigne E, Chaves M, Rossi J D. Asymptotic behavior for nonlocal diffusion equations, J. Math. Pures Appl., 2006, 86(3): 271-291.

[23] Zhang G, Li W, Sun Y. Asymptotic behavior for nonlocal dispersal equations, Nonlinear Anal., 2010, 72(12): 4466-4474.

[24] Hetzer G, Nguyen T, Shen W. Coexistence and extinction in the Volterra-Lotka competition model with nonlocal dispersal, Commun. Pure Appl. Anal, 2012, 11: 1699-1722.

[25] Hutson V, Shen W, Vickers G T. Spectral theory for nonlocal dispersal with periodic or almostperiodic time dependence, Rocky Mountain J. Math., 2008: 1147-1175.

[26] Ruan S. Spatial-temporal dynamics in nonlocal epidemiological models, Mathematics for life science and medicine, 2007: 97-122.

[27] Li W, Yang F. Traveling waves for a nonlocal dispersal SIR model with standard incidencee, J. Integral Equations Appl., 2014: 243-273.

[28] Li F, Lou Y, Wang Y. Global dynamics of a competition model with non-local dispersal I: The shadow system, J. Math. Anal. Appl., 2014, 412(1): 485-497.

[29] Han B, Yang Y, Bo W, et al. Global dynamics of a Lotka-Volterra competition diffusion system with nonlocal effects, Int. J. Bifurcation Chaos Appl., 2020, 30(05): 2050066.

[30] Wang J, Wu C. Forced waves and gap formations for a Lotka-Volterra competition model with nonlocal dispersal and shifting habitats, Nonlinear Anal. RWA, 2021, 58: 103208.

[31] Sun J, Yang F, Li W. A nonlocal dispersal equation arising from a selection-migration model in genetics, J. Diff. Equ., 2014, 257(5): 1372-1402.

[32] Berestycki H, Coville J, Vo H H. Persistence criteria for populations with non-local dispersion, J. Math. Biol., 2016, 72: 1693-1745.

[33] Su Y, Li W, Yang F. Effects of nonlocal dispersal and spatial heterogeneity on total biomass, Discrete Contin. Dyn. Syst. Ser. B, 2019, 24: 4929-4936.

[34] Sun J. Effects of dispersal and spatial heterogeneity on nonlocal logistic equations, Nonlinearity, 2021, 34(8): 5434-5455.

[35] MUller K. Investigations on the organic drift in North Swedish streams, Rep. Inst. Fresh-wat. Res., 1954, 35: 133-148.

[36] Speirs D, Gurney W. Population persistence in rivers and estuaries, Ecology, 2001, 82(5): 1219- 1237.

[37] Murray J, Sperb R. Minimum domains for spatial patterns in a class of reaction diffusion equations, J. Math. Biol., 1983, 18(2):169-184.

[38] Belgacem F, Cosner C, The effects of dispersal along environmental gradients on the dynamics of populations in heterogeneous environment, Can. Appl. Math. Qua., 1995, 3(4):379-397.

[39] Lou Y, Zhou P, Evolution of dispersal in advective homogeneous environment: The effect of boundary conditions, J. Differ. Equ., 2015, 259(1):141-171.

[40] Lou Y, Zhao X, Zhou P, Global dynamics of a Lotka-Volterra competition-diffusion-advection system in heterogeneous environments, J. Math. Pures Appl., 2019, 121: 47-82.

[41] Zhao X, Zhou P. On a Lotka-Volterra competition model: the effects of advection and spatial variation, Calc. Var. Partial Differ. Equ., 2016, 55(4):73

[42] Coville J. On uniqueness and monotonicity of solutions of non-local reaction diffusion equation, Ann. Mat. Pura Appl., 2006, 185: 461-485.

[43] Zhang G, Zhao X. Propagation dynamics of a nonlocal dispersal Fisher-KPP equation in a timeperiodic shifting habitat, J. Diff. Equ., 2020, 268(6): 2852-2885.

[44] De Leenheer P, Shen W, Zhang A. Persistence and extinction of nonlocal dispersal evolution equations in moving habitats, Nonlinear Anal. RWA, 2020, 54: 103-110.

[45] Shen W, Xie X. On principal spectrum points/principal eigenvalues of nonlocal dispersal operators and applications, Discrete Contin. Dyn. Syst., 2015, 35 (4): 1665-1696.

[46] Li F, Coville J, Wang X. On eigenvalue problems arising from nonlocal diffusion models, Discrete Contin. Dyn. Syst A, 2017, 37(2): 879-903.

[47] Evans, L. C. Partial differential equations: second edition. Wadsworth & Brooks/cole Mathematics, 2010, 19(1), 211-223.

[48] Pudelko A. Rarefaction waves in nonlocal convection-diffusion equations, Colloq. Math., 2014, 137(1): 27-42.

[49] Simon J. Compact sets in the space Lp(0, T; B), Ann. Mat. Pura Appl., 1986, 146: 65-96.

[50] Tang Y, Dai B. A nonlocal reaction-diffusion-advection model with free boundaries,preprint.

[51] Karch G. Nonlinear evolution equations with anomalous diffusion, Jindrich Necas Center for Mathematical Modeling Lecture notes, 2009, pp 25-68.

[52] Wang M. Nonlinear second order parabolic equations, CRC Press, 2021.

[53] Ball J M, Geometric Theory of Semi-linear Parabolic Equations, in: Lecture Notes in Math., vol. 840, Springer-Verlag, Berlin, 1982, 14.

[54] Pazy A. Semigroups of linear operators and applications to partial differential equations, Springer Science & Business Media, 2012.

[55] Coville J, Hamel F. On generalized principal eigenvalues of nonlocal operators with a drift, Nonlinear Anal., 2020, 193: 111569.

[56] Coville J. Can a population survive in a shifting environment using non-local dispersion, Nonlinear Anal., 2021, 212: 112416.

[57] Shen W, Zhang A. Spreading speeds for monostable equations with nonlocal dispersal in space periodic habitats, J. Diff. Equ., 2010, 249(4): 747-795.

:::info
Authors:

(1) Yaobin Tang, School of Mathematics and Statistics, HNP-LAMA, Central South University, Changsha, Hunan 410083, P. R. China;

(2) Binxiang Dai, School of Mathematics and Statistics, HNP-LAMA, Central South University, Changsha, Hunan 410083, P. R. China ([email protected]).

:::

:::info
This paper is available on arxiv under CC BY 4.0 DEED license.

:::