The Math Behind Persistence and Extinction in Freshwater Ecosystems | HackerNoon

:::info
Authors:

(1) Yaobin Tang, School of Mathematics and Statistics, HNP-LAMA, Central South University, Changsha, Hunan 410083, P. R. China;

(2) Binxiang Dai, School of Mathematics and Statistics, HNP-LAMA, Central South University, Changsha, Hunan 410083, P. R. China ([email protected]).

:::

Table of Links

Abstract and 1. Introduction

2. The well-posed global solution

3. Nontrivial stationary solution

   3.1 Spectral theory of integro-differential operator

   3.2 The existence, uniqueness and stability of nontrivial stationary solution

4. The sharp criteria for persistence or extinction

5. The limiting behaviors of solutions with respect to advection

6. Numerical simulations

7. Discussion, Statements and Declarations, Acknowledgement, and References

Abstract

This paper is devoted to a nonlocal reaction-diffusion-advection model that describes the spatial dynamics of freshwater organisms in a river with a directional motion. Our goal is to investigate how the advection rate affects the dynamic behaviors of species. We first establish the well-posedness of global solutions, where the regularized problem containing a viscosity term and the re-established maximum principle play an important role. And we then show the existence/nonexistence, uniqueness, and stability of nontrivial stationary solutions by analyzing the principal eigenvalue of integrodifferential operator (especially studying the monotonicity of the principal eigenvalue with respect to the advection rate), which enables us to understand the longtime behaviors of solutions and obtain the sharp criteria for persistence or extinction. Furthermore, we study the limiting behaviors of solutions with respect to the advection rate and find that the sufficiently large directional motion will cause species extinction in all situations. Lastly, the numerical simulations verify our theoretical proofs.

1 Introduction

The dispersal ways of populations have received much attention recently and are a major focus of most scholars. The reaction-diffusion equation is a mathematical model commonly used to describe the spatial random diffusion and evolution of biological populations or diseases [1–3].

Denote Ω ⊂ R is a smooth domain. If the dispersal takes place in R and species u vanishes outside Ω, then

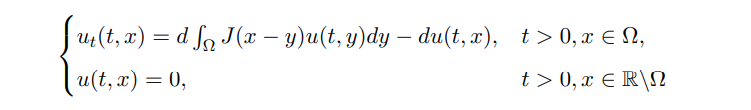
is called the nonlocal diffusion equation with homogeneous Dirichlet boundary condition [8, 9]. Biologically, the region Ω outside is considered a hostile environment, and any individual that jumps outside of Ω dies instantly. Note that the boundary condition is not understood in the usual sense, as we are not imposing that u|∂Ω = 0.

If it takes into account the diffusion inside Ω, as we have explained, no individual enters or leaves the domain Ω, then

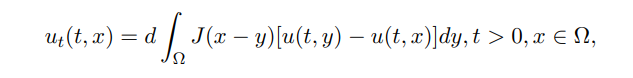
is called the nonlocal diffusion equation with classical Neumann boundary condition in the literature [10, 11].

There are a lot of researches on nonlocal diffusion problems in biomathematics. In recent years, the following nonlocal evolution equation

In addition, some researchers are devoted to the nonlocal problem with a Fisher-KPP type, bistable type or general nonlinear reaction term. Specifically, Bates & Zhao [18] investigated the spatial dynamics of organisms or cells. To be specific, they considered the following model:

In addition to the spatial diffusion of populations, various environmental factors such as wind direction, river flow, climate, and resource distribution can influence the longtime dynamic behaviors of biological populations and diseases. To account for this phenomenon, researchers include an advection term to describe the directed movement of the population or disease over space.

In 1954, Muller [35] observed that organisms living in streams or rivers are constantly washed downstream or out of the original ecological environment, resulting in a general decline in species, even extinction. But some species can survive in this environment from generation to generation, and this biological phenomenon often is called ”drift paradox”. So they puzzled over a question: How do species in rivers survive without being washed away? Then, Speirs & Gurney introduced the reaction-advection-diffusion equation in [36] to describe the dynamic behaviors of single species under the influence of currents:

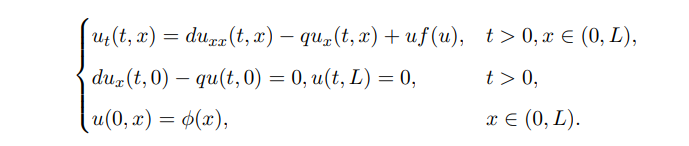
The biological explanation for this is that the population u not only undergoes random diffusion but also experiences advective transport at velocity q. They demonstrated that a large enough random diffusion can counterbalance the directional motion caused by currents, leading to the survival of species. Subsequently, the persistence of single or multiple populations in advective environments was studied [37–41]. Some significant and profound results have been obtained for reaction-diffusion problems in advective environments. However, the question remains whether these results can be extended to nonlocal diffusion problems in advective environments. As far as the author knows, in [42], the monotonicity and uniqueness of positive solutions of integro-differential equation

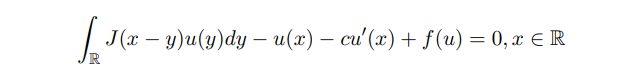
was studied. Its positive solution can be regarded as the traveling wave solution u(t, x) = φ(x + ct) for the following nonlocal problem:

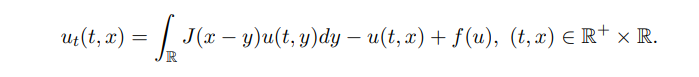
Then, Zhao & Shen et al. [43, 44] discussed a nonlocal reaction-diffusion equation in shifting habitat:

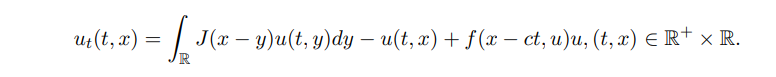
Biologically, it represents that the population will change with the moving habitat of speed c due to climate change. Considering the function v(t, ζ) that satisfies the form u(t, x) = v(t, x − ct) with v(t, x) being differentiable and ζ = x − ct, we find that v(t, ζ) satisfies

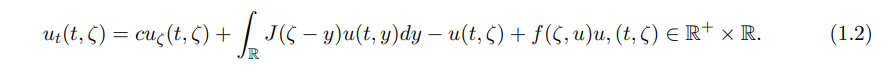
And then, the nonexistence/existence of nontrivial stationary solutions of (1.2) was obtained by studying the spectral theory of integro-differential operator:

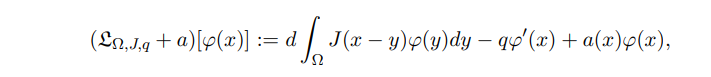
which was studied by [20, 32, 44, 45].

In addition, observe that [46] considered fresh water organisms living in a river domain Ω = (l1, l2). Assume that these organisms not only can move within the river due to random diffusion, but are also subject to directed movement arising from currents. Concretely, these organisms are affected by the velocity of currents from left to right and they can not survive on land (−∞, l1) and in the ocean (l2, +∞):

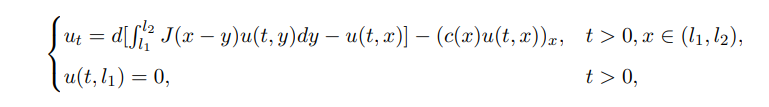
where c(x) > 0 on [l1, l2] is the velocity function of water. They emphasized the importance of boundary condition u(t, l1) = 0 for t > 0, which ensures that the initial value problem is well-posed. Their paper mainly discussed the spectrum of the linearized problem, and studied the sign of principal eigenvalue.

In this paper, we still consider fresh water organisms living in a river domain Ω = (l1, l2) and intend to study the spatial dynamics behaviors of fresh water organisms in advective environment. If we further assume that these organisms can not enter or leave the domain Ω and are affected by the velocity q of currents from left to right, then we study the following nonlocal Neumann advection-diffusion model:

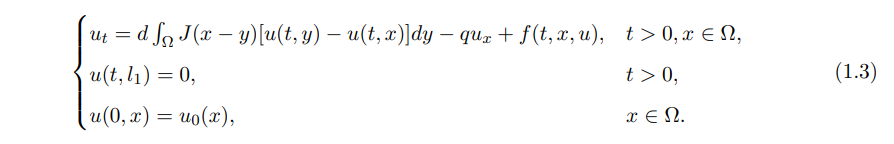
If we further assume that these organisms are affected by the velocity q of currents from left to right and they can not survive on land (−∞, l1) and in the ocean (l2, +∞). Then, we study the following nonlocal Dirichlet advection-diffusion model:

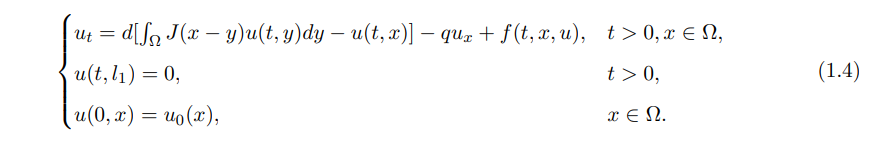
Here Ω is a bounded open domain, q > 0 is the advection rate and the initial function u0(x) satisfies

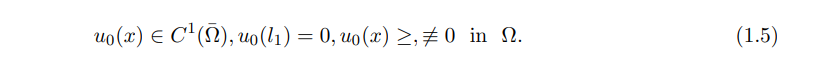
Remark 1.1. (1) The boundary condition u(t, l1) = 0 for t > 0 is to ensure the initial value problem is well-posed. In fact, the equation (1.3) or (1.4) are essentially a perturbation of a transport equation by an integral operator. When d ≡ 0, we find that the equation is a transport equation in a bounded domain, which need a boundary condition to ensure the well-posedness of solution.

(2) If these organisms are affected by the velocity q of currents from right to left, the boundary condition will be rewritten as u(t, l2) = 0 for t > 0. Its discussion is similar to the analysis of (1.3) or (1.4).

The purpose of this paper is to show the existence and uniqueness of global solutions, the existence/nonexistence, uniqueness and stability of nontrivial stationary solutions, the longtime behaviors of solutions, and get the sharp criteria for persistence or extinction. In addition, the effects of advection rate on the dynamic behaviors of solutions will be discussed.

The remaining parts of this paper are organized as follows. Section 2 is devoted to studying the existence and uniqueness of solutions for (1.3) and (1.4). In Section 3, the existence/nonexistence, uniqueness and stability of nontrivial stationary solutions are obtained. In Section 4, the criteria for persistence or extinction are formulated. And in Section 5, the limiting profiles of solution with respect to advection rate q are considered. The last section gives a brief discussion.

2 The well-posed global solution

For convenience, we set

In order to obtain the existence of solutions for nonlocal Neumann problem (1.3), we must consider the following linear problem:

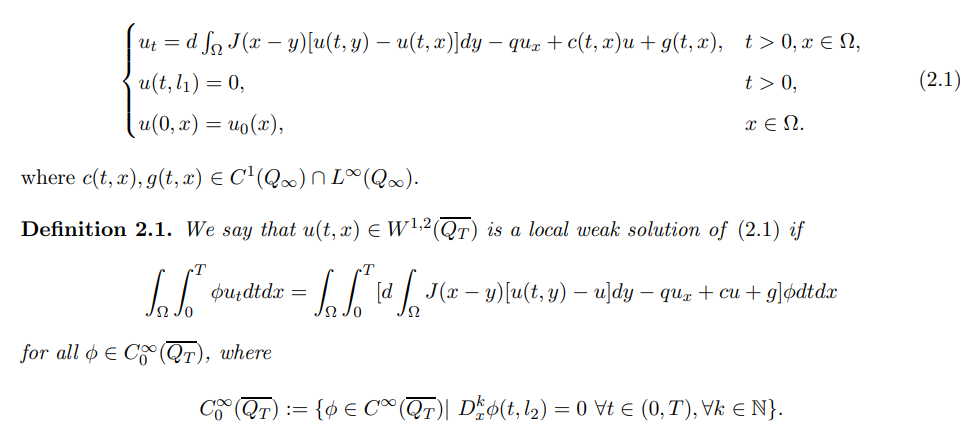
Due to the lack of compactness and regularity of nonlocal operators, many classical methods cannot be used directly to nonlocal dispersal problems. To overcome these difficulties, we shall consider the following problem regularized by the usual viscosity term:

Since it follows from [47, Theorem 2, Chapter 5.9.2] that

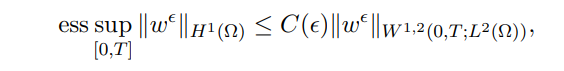
we have the following estimation

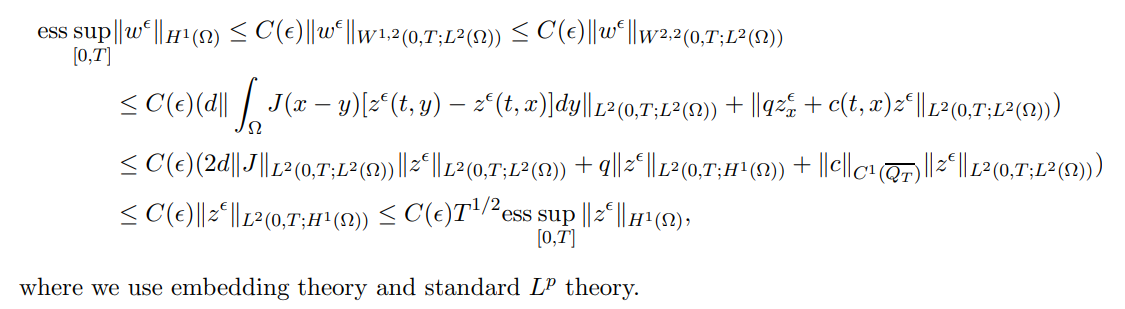
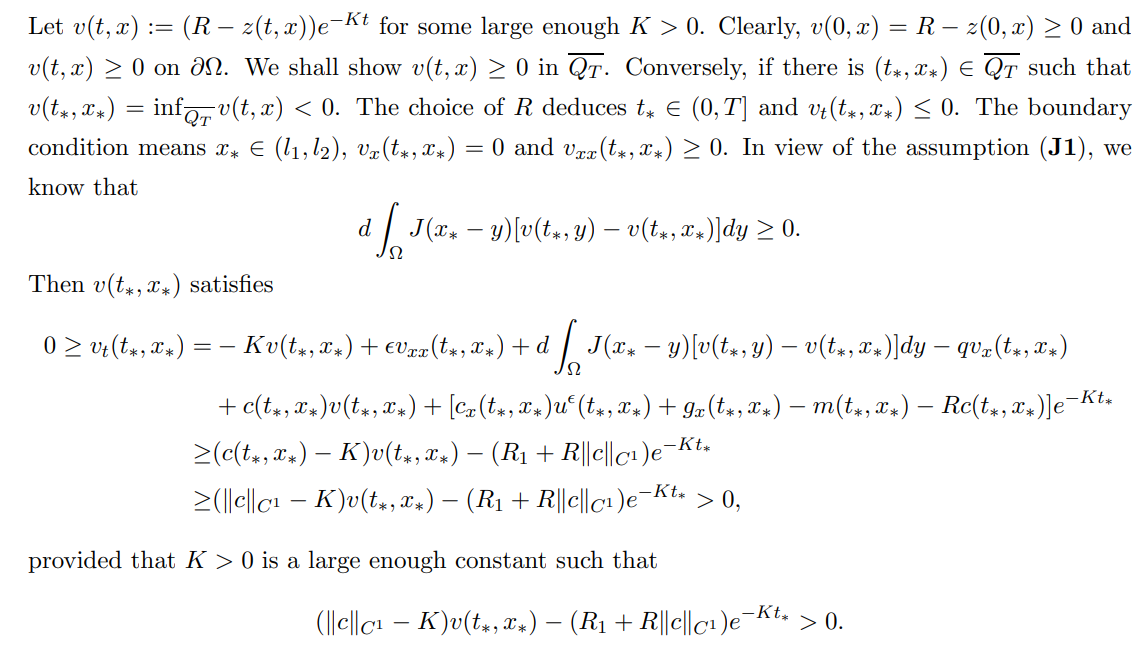
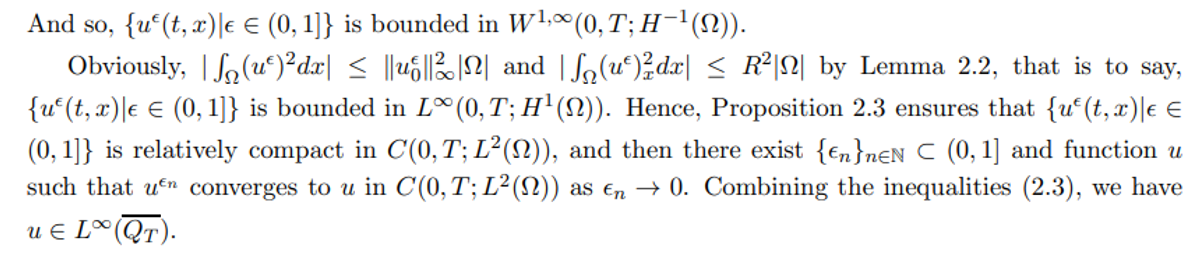
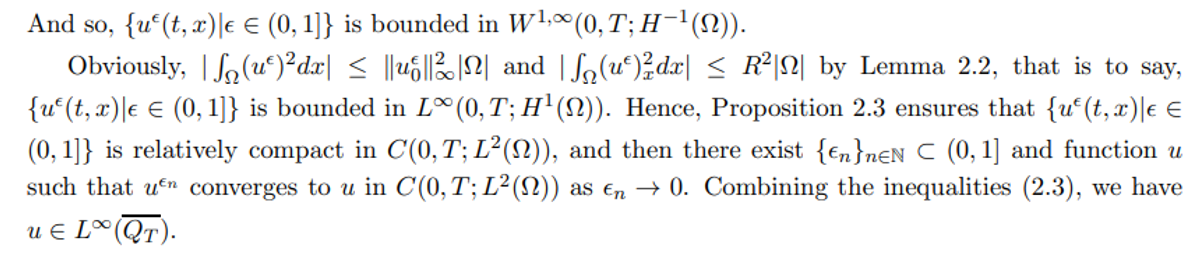
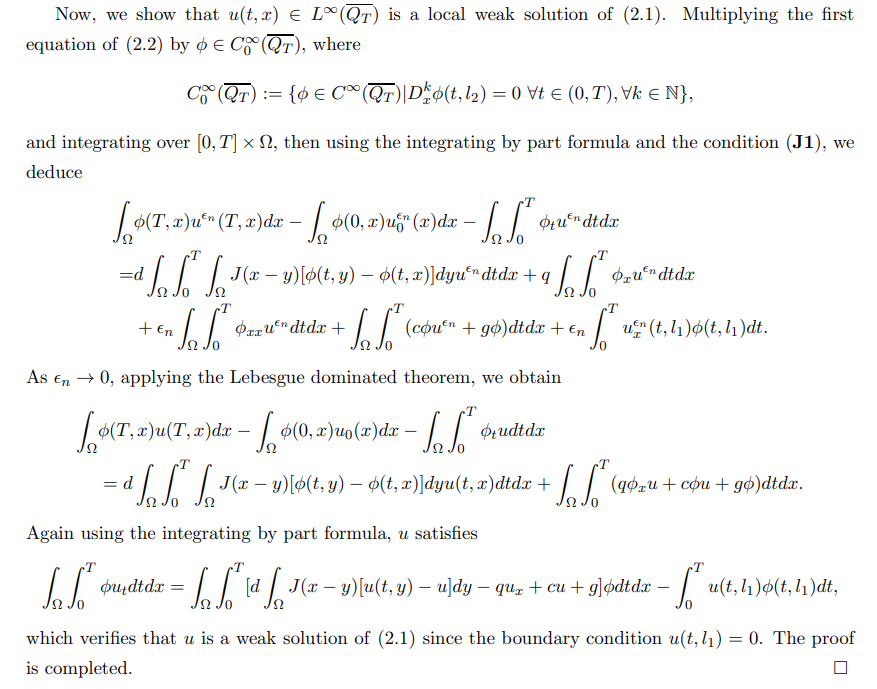
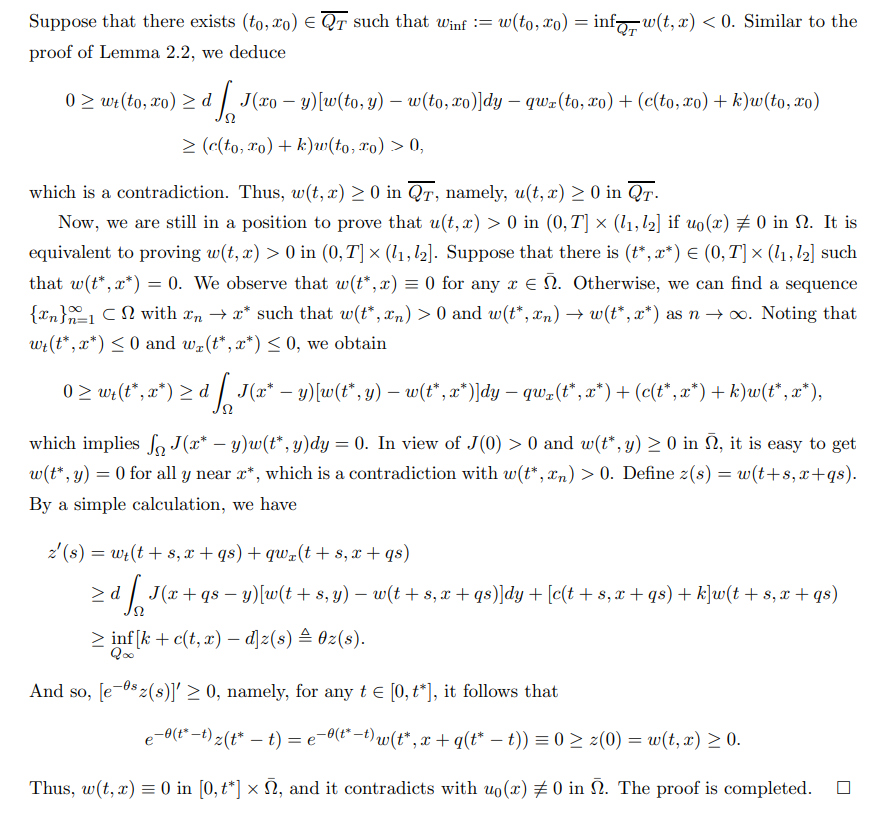
In the followings, we shall apply the upper and lower solution methods to get the existence of solutions of (1.3), so we define the upper and lower solutions as follows:

Combining with Lemma 2.6, naturally, it gives a ordering of upper solution and lower solution:

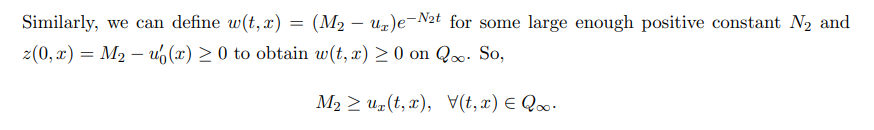
The proof is completed.

And we can use the same methods to consider the nonlocal Dirichlet problem (1.4). On the one hand, we can establish the maximum principle for (1.4):

:::info
This paper is available on arxiv under CC BY 4.0 DEED license.

:::