The Tortoise and the Hare: An Unexpected Scheduling Race Between MILP and CP Solvers | HackerNoon

Abstract and 1. Introduction

2. Mixed integer and constraint programming models

   2.1 Mixed-integer linear programming model

   2.2 Constraint Programming model

3. Constructive Heuristics

4. Benchmark instances

5. Numerical experiments

   5.1 Experiments with the constructive heuristics

   5.2 Solving the proposed models with a commercial solver

6. Conclusions and References

5.2 Solving the proposed models with a commercial solver

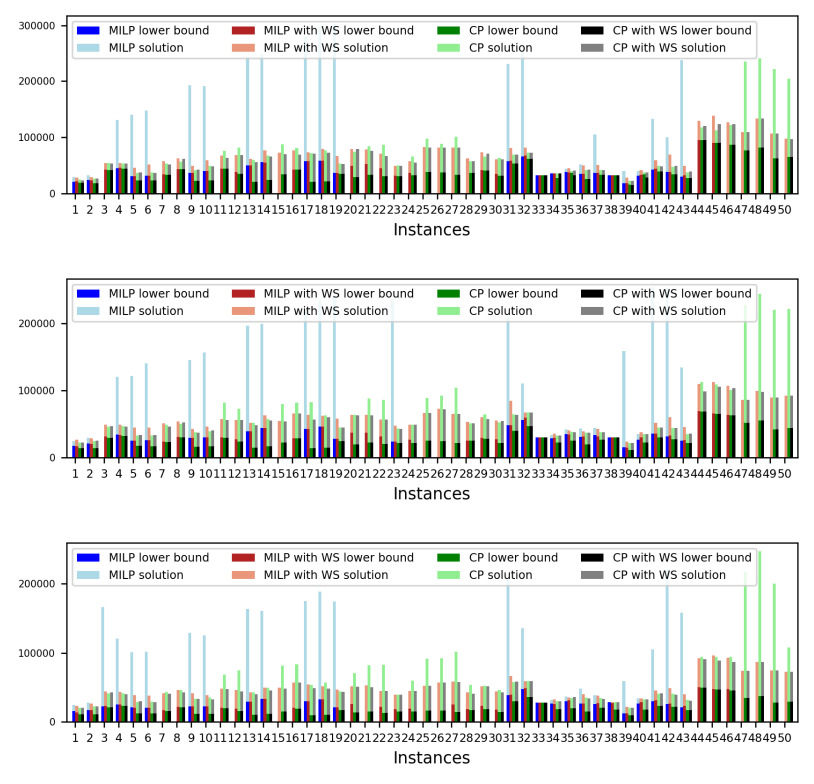
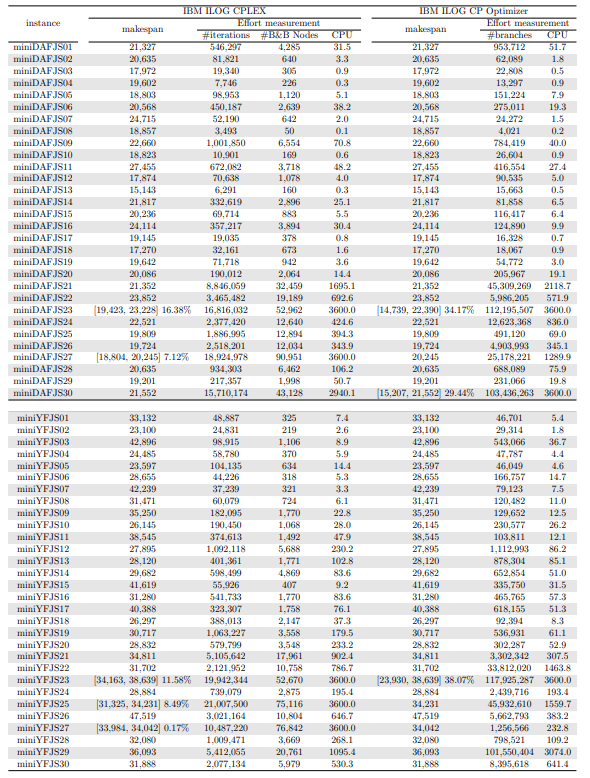
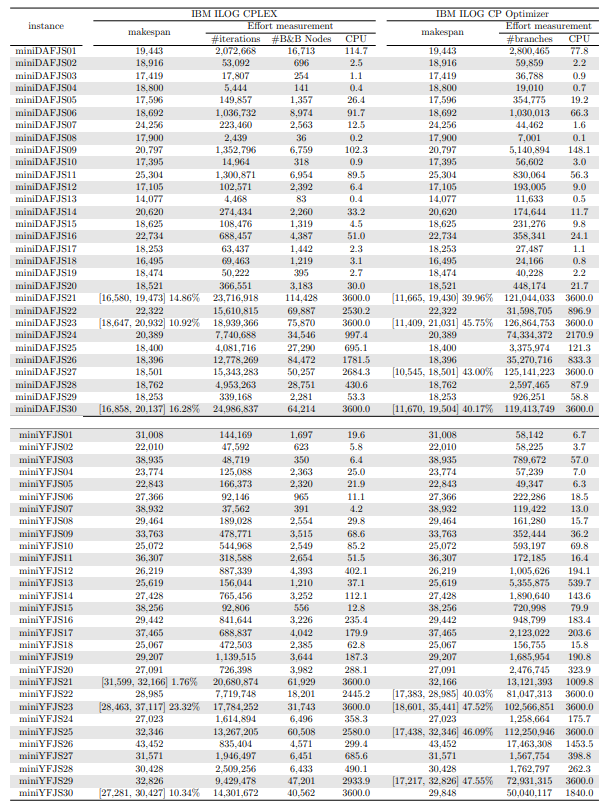
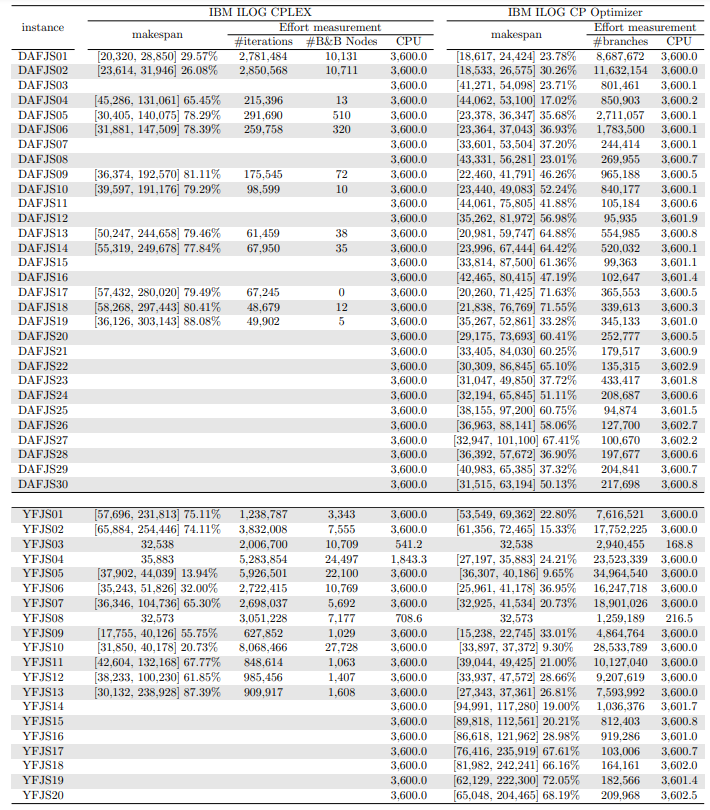
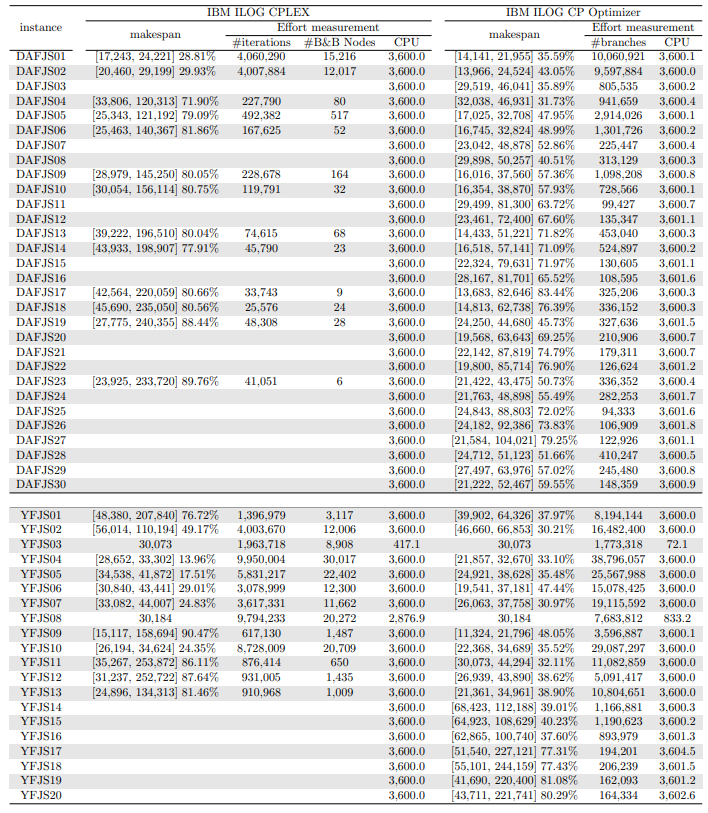
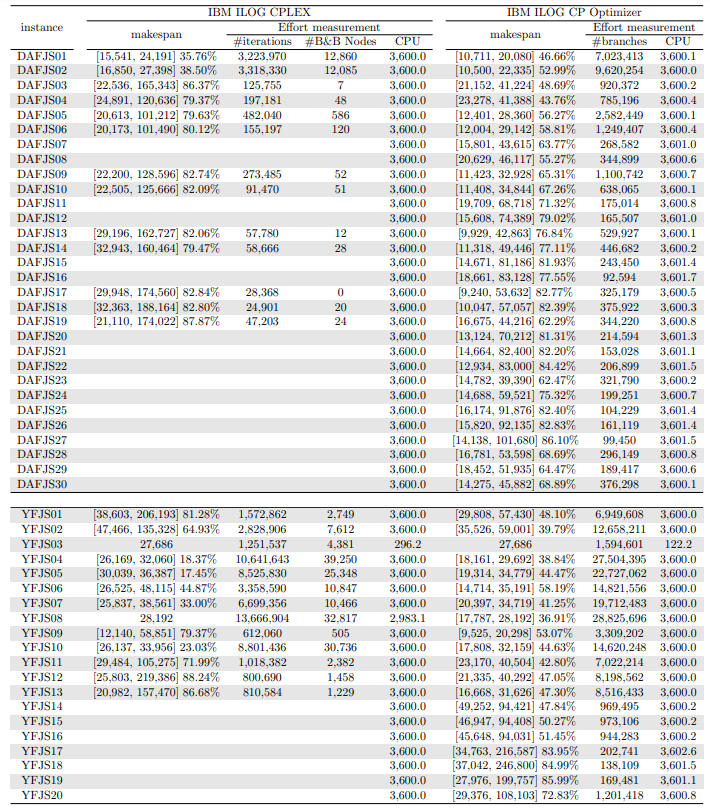
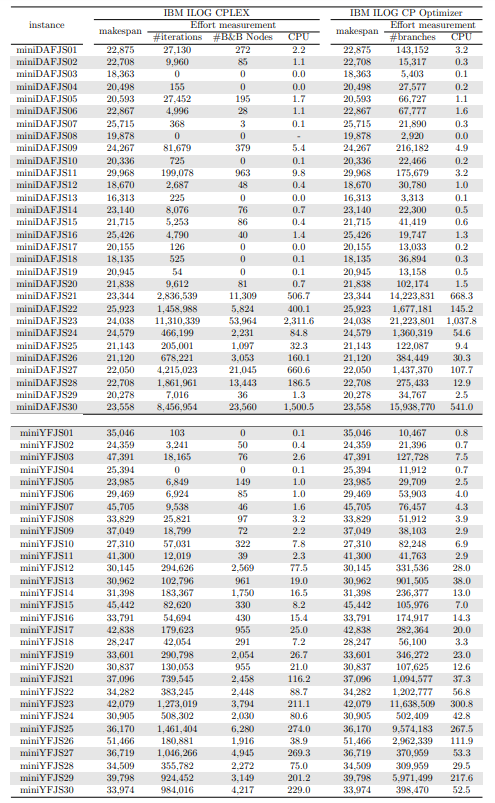
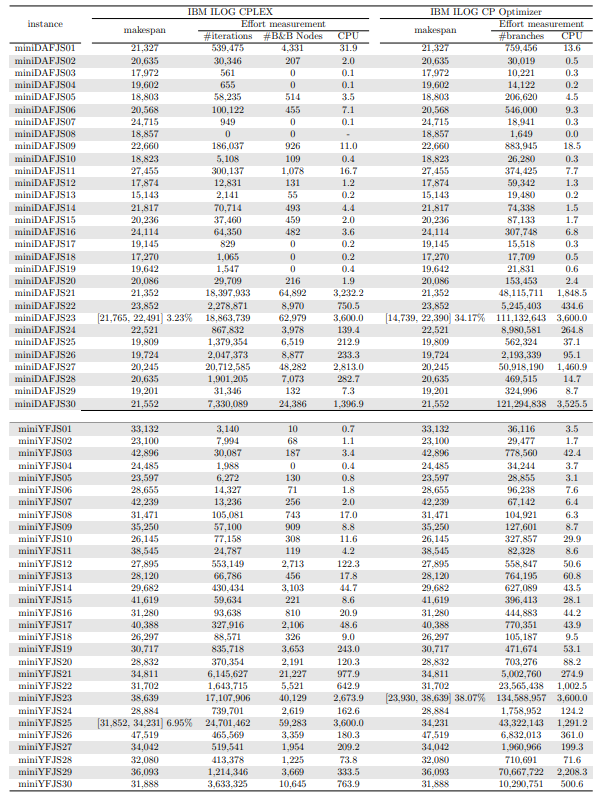
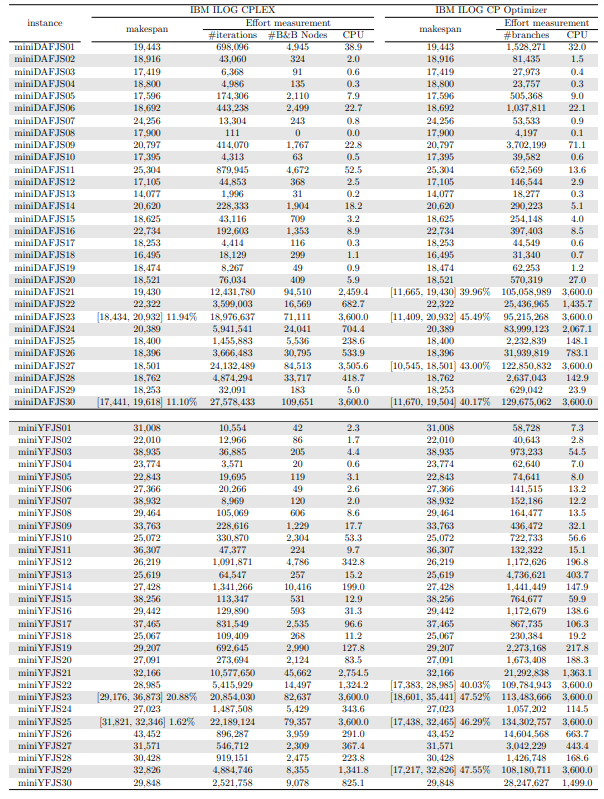
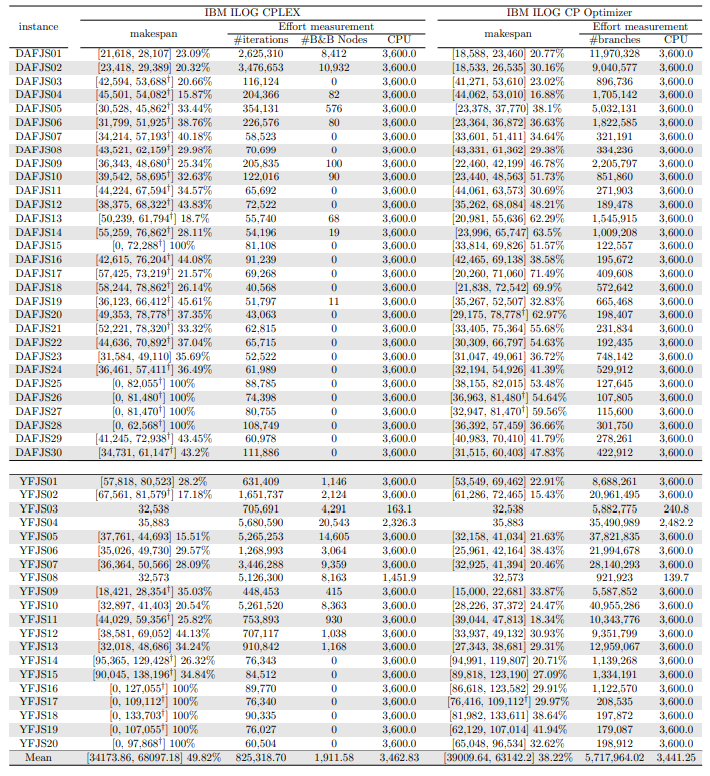
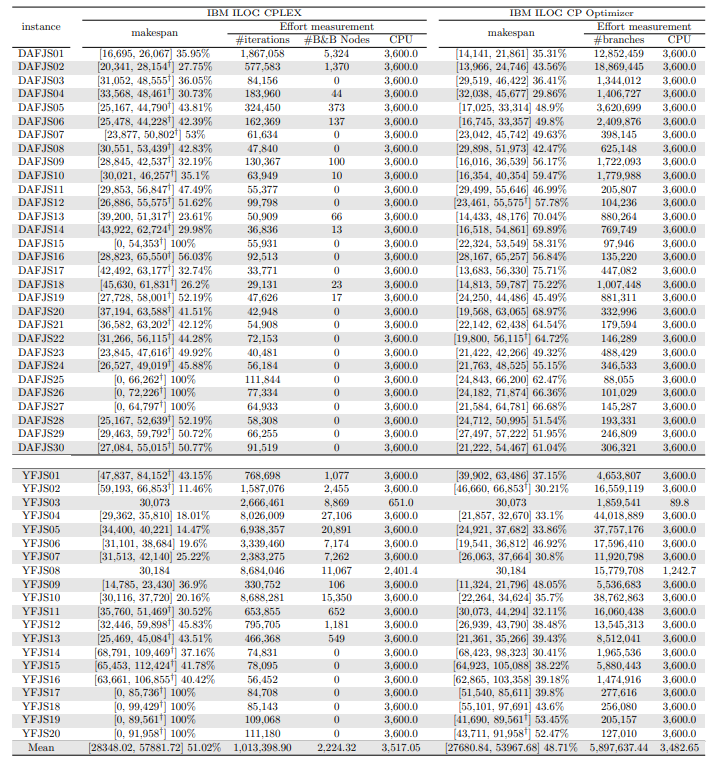
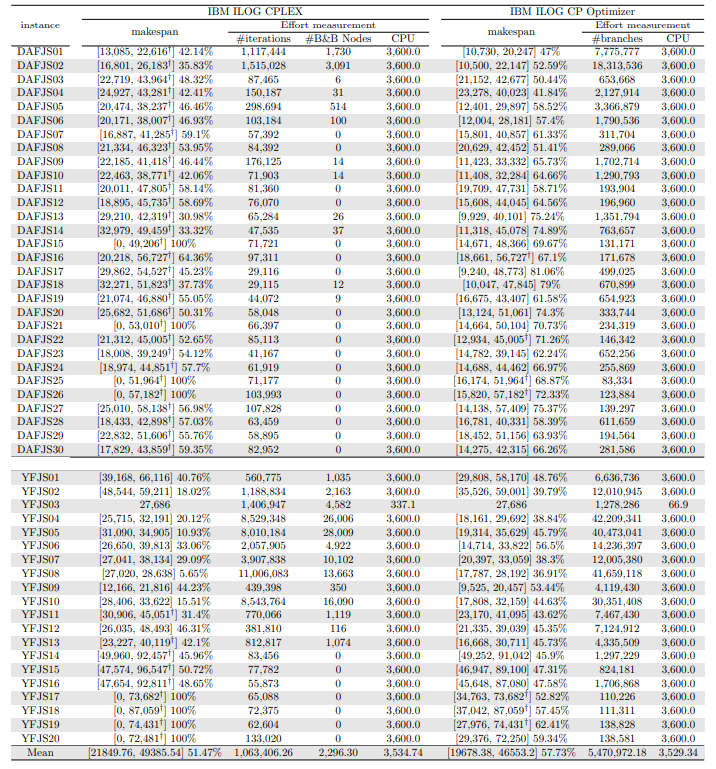
In this section, we apply an exact solver to the 330 instances considered and evaluate the quality of the solutions found within a given CPU time limit, depending on whether we provide the solution found by the constructive heuristics as an initial solution or not. Since there is no clear winner between the two constructive heuristics and their execution time is negligible, we run both and give the best of the two as initial solution to the exact solver. In the tables and figures, the solvers’ runs that receive as input a solution computed by one of the constructive heuristics are identified with the expression “warm start”.

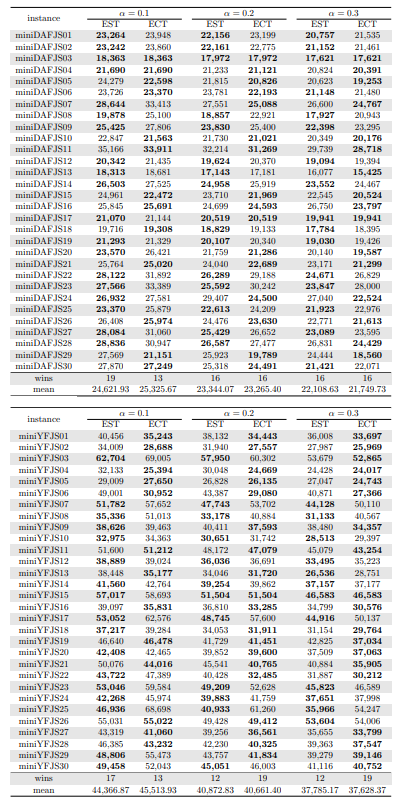
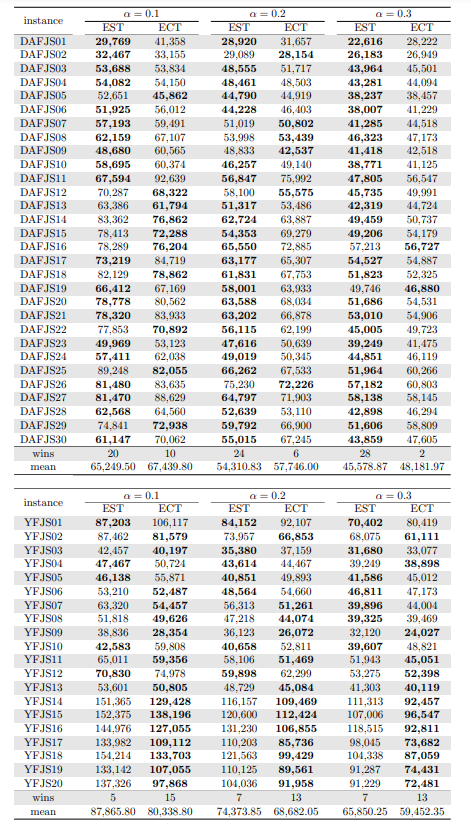
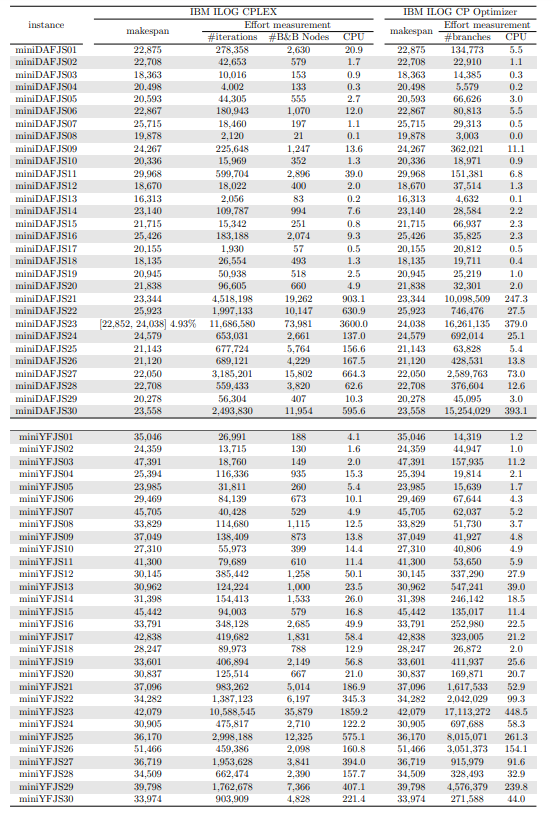
Tables 5, 6, 7, 8, 9, and 10 show the results in detail when the warm start is not taken into account. Tables 5, 6, and 7 correspond to the small-sized instances with α equal to 0.1, 0.2, and 0.3, respectively; while Tables 8, 9, and 10 show the same thing for the large-sized instances. Tables 11–16 show the results when the warm start is taken into account. The tables show the information related to the resolution of the MILP and CP models. When a single number appears in the “makespan” column, it means that a provably optimal solution with that makespan value was found. When instead of a number an expression of the form [A, B] C% appears, it means that a feasible solution was found with value B for the makespan, value A for a lower bound on the makespan, and gap C equal to 100(B − A)/B. As measures of computational effort, for the MILP solver the tables show the number of iterations, the number of nodes explored in the branch-and-bound search tree, and the CPU time in seconds. For the CP solver, the tables show the number of branches and the CPU time in seconds. If no information is displayed for a particular instance, it means that the solver was unable to find a feasible solution within the specified CPU time limit. In Tables 11–16, which show results with warm start, the symbol † next to the optimal or best value found means that the exact method returned exactly the same solution computed with the constructive heuristic and given as initial solution. The information from Tables 11–16 is presented graphically in Figure 6.

Let’s look at the small-sized instances first. Without warm start, the exact methods found provably optimal solutions for 168 instances of the MILP model and 169 instances of the CP model (out of a total of 180 small-sized instances). In the remaining cases, the gaps for the MILP model instances were between 0.17% and 23.32%, while for the CP model instances the gaps were between 29.44% and 47.55%. It is worth noting that in the few cases without a proven optimal solution, there is a slight advantage in the best solution found for the CP model instances and a slight advantage in the lower bounds found for the MILP model instances. In the instances where a proven solution was found by solving both the MILP model and the CP model, the CP solver was on average 12.09% faster than the MILP solver. When the constructive heuristics solution is made available to the exact solvers, the number of proven optimal solutions found hardly changes (still the same number for MILP model instances and one less for CP model instances, not necessarily the same as those solved without the warm start). However, for MILP model instances where a proven optimal solution is found both with and without warm start, the use of warm start reduces the solution time by 32.52% in average. This reduction is 4.44% for the CP model solver. One way or another, whether using the MILP model or the CP model, with or without warm start, it was possible to find provably optimal solutions in 176 (out of 180) small-sized instances.

The analysis of the 150 large-sized instances is a little different. Without a warm start, the exact methods were able to find proven optimal solutions for only 7 instances of the MILP model and 5 instances of the CP model. In 70 MILP model instances it was possible to find feasible solutions with gaps between 13.94% and 90.47%, while feasible solutions with gaps between 9.30% and 86.10% were found in 145 instances of the CP model. In 73 instances of the MILP model, not a single feasible solution was found. In the 70 instances in which feasible solutions from both the MILP and CP models were found, the solutions found using the CP model were on average 68.85% better. It was after observing these results that the idea arose to develop constructive heuristics to test the warm start and consider a set of smaller instances.

When the solution of the constructive heuristics is fed to the exact solver, 6 provably optimal solutions and 144 feasible solutions are obtained with gaps between 5.65% and 64.36% for MILP model instances. For the CP model instances, the same number of provably optimal and feasible solutions are found, with gaps between 15.43% and 81.06% for the feasible ones. In those instances where a proven optimal solution is found without and with warm start, warm start increases the computational cost of solving the MILP and CP models by 9.69% and 25.99%, respectively. On the other hand, in the MILP model instances in which a feasible solution was found without the use of warm start, the use of warm start improved the quality of the feasible solution found by 49.46%. For the CP model instances, this improvement was 11.53%. In the 144 instances in which feasible solutions from both the MILP and CP models were found, the solutions found using the CP model were on average 6.82% better. The question remains as to whether the exact methods are able to improve the solution provided by the constructive heuristics or whether the statistics improve only because the solvers return the solution they received as input. In the case of the MILP model instances, the initial solution is improved in 33 problems, while in the CP model instances the initial solution is improved in 134 problems. Without a warm start, in the instances where it is possible to find a provably optimal solution for both the MILP model and the CP model (5 instances), the cost of solving the CP models is 70.81% lower. In the case where provably optimal solutions are found in both cases using warm start (6 instances), the cost of solving the CP models is 41.86% lower. In short, it is challenging to find a proven optimal solution for large-sized instances, solving CP model instances costs less, CP models provide better quality feasible solutions when it is not possible to find a provably optimal solution, and solving MILP models provides better quality lower bounds. One way or another, whether using the MILP model or the CP model, with or without warm start, it was possible to find provably optimal solutions in only 7 large-sized instances and feasible solutions in all the remaining 143 large-sized instances.

6 Conclusions

In this work, we addressed the FJS scheduling problem with sequencing flexibility and positionbased learning effect. To the authors’ knowledge, this combination, with potential application in a wide range of real-world industrial environments, has never been addressed in the literature. As a first step towards its efficient and effective solution, we introduced a set of 110 instances that transform into 330 instances by varying the learning rate α ∈ {0.1, 0.2, 0.3}. By introducing MILP and CP models, an exact solver aided by constructive heuristics was able to provide 183 proven optimal solutions. Instances, their solutions, models and constructive heuristics are all available for download at https://github.com/kennedy94/FJS. We expect this benchmark test-set to guide the introduction and evaluation of new effective heuristic and metaheuristic approaches for the considered problem. In fact, this is the current line of research of the authors.

Conflict of interest statement: On behalf of all authors, the corresponding author states that there is no conflict of interest.

Data availability: The datasets generated during and/or analysed during the current study are available in the GitHub repository, https://github.com/kennedy94/FJS.

References

[1] R. Alvarez-Valdes, A. Fuertes, J. M. Tamarit, G. Gim´enez, and R. Ramos. A heuristic to schedule flexible job-shop in a glass factory. European Journal of Operational Research, 165(2):525–534, 2005.

[2] J. L. Andrade-Pineda, D. Canca, P. L. Gonzalez-R, and M. Calle. Scheduling a dualresource flexible job shop with makespan and due date-related criteria. Annals of Operations Research, 291(1):5–35, 2020.

[3] A. Azzouz, M. Ennigrou, and L. Ben Said. Scheduling problems under learning effects: classification and cartography. International Journal of Production Research, 56(4):1642– 1661, 2017.

[4] E. G. Birgin, P. Feofiloff, C. G. Fernandes, E. L. De Melo, M. T. I. Oshiro, and D. P. Ronconi. A MILP model for an extended version of the flexible job shop problem. Optimization Letters, 8(4):1417–1431, 2014.

[5] E. G. Birgin, J. E. Ferreira, and D. P. Ronconi. List scheduling and beam search methods for the flexible job shop scheduling problem with sequencing flexibility. European Journal of Operational Research, 247(2):421–440, 2015.

[6] D. Biskup. Single-machine scheduling with learning considerations. European Journal of Operational Research, 115(1):173–178, 1999.

[7] D. Biskup. A state-of-the-art review on scheduling with learning effects. European Journal of Operational Research, 188(2):315–329, 2008.

[8] Z.-C. Cao, C.-R. Lin, and M.-C. Zhou. A knowledge-based cuckoo search algorithm to schedule a flexible job shop with sequencing flexibility. IEEE Transactions on Automation Science and Engineering, 18(1):56–69, 2021.

[9] T. C. E. Cheng and G. Wang. Single machine scheduling with learning effect considerations. Annals of Operations Research, 98(1/4):273–290, 2000.

[10] T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein. Introduction to Algorithms. The MIT Press, Cambridge, MA, USA, 4th edition, 2022.

[11] P. Y. Gan and K. S. Lee. Scheduling of flexible-sequenced process plans in a mould manufacturing shop. The International Journal of Advanced Manufacturing Technology, 20(3):214– 222, 2002.

[12] J. Gao, M. Gen, and L. Sun. Scheduling jobs and maintenances in flexible job shop with a hybrid genetic algorithm. Journal of Intelligent Manufacturing, 17(4):493–507, 2006.

[13] M. R. Garey, D. S. Johnson, and R. Sethi. The complexity of flowshop and jobshop scheduling. Mathematics of Operations Research, 1(2):117–129, 1976.

[14] J. N. D. Gupta and S. K. Gupta. Single facility scheduling with nonlinear processing times. Computers and Industrial Engineering, 14(4):387–393, 1988.

[15] A. Janiak, T. Krysiak, and R. Trela. Scheduling problems with learning and ageing effects: A survey. Decision Making in Manufacturing and Services, 5(1):19–36, 2011.

[16] G. A. Kasapidis, S. Dauzere-Pees, D. C. Paraskevopoulos, P. P. Repoussis, and C. D. Tarantilis. On the multiresource flexible job-shop scheduling problem with arbitrary precedence graphs. Production and Operations Management, 32(7):2322–2330, 2023.

[17] G. A. Kasapidis, D. C. Paraskevopoulos, P. P. Repoussis, and C. D. Tarantilis. Flexible job shop scheduling problems with arbitrary precedence graphs. Production and Operations Management, 30(11):4044–4068, 2021.

[18] Y. K. Kim, K. Park, and J. Ko. A symbiotic evolutionary algorithm for the integration of process planning and job shop scheduling. Computers and Operations Research, 30(8):1151– 1171, 2003.

[19] P. Laborie, J. Rogerie, P. Shaw, and P. Vil´ım. IBM ILOG CP optimizer for scheduling: 20+ years of scheduling with constraints at ibm/ilog. Constraints, 23(2):210–250, 2018.

[20] J. Y.-T. Leung, H. Li, and M. Pinedo. Order scheduling in an environment with dedicated resources in parallel. Journal of Scheduling, 8(5):355–386, 2005.

[21] W. T. Lunardi, E. G. Birgin, P. Laborie, D. P. Ronconi, and H. Voos. Mixed integer linear programming and constraint programming models for the online printing shop scheduling problem. Computers and Operations Research, 123:105020, 2020.

[22] W. T. Lunardi, E. G. Birgin, D. P. Ronconi, and H. Voos. Metaheuristics for the online printing shop scheduling problem. European Journal of Operational Research, 293(2):419– 441, 2021.

[23] G. Vilcot and J.-C. Billaut. A tabu search and a genetic algorithm for solving a bicriteria general job shop scheduling problem. European Journal of Operational Research, 190(2):398–411, 2008.

[24] A. Vital-Soto, A. Azab, and M. F. Baki. Mathematical modeling and a hybridized bacterial foraging optimization algorithm for the flexible job-shop scheduling problem with sequencing flexibility. Journal of Manufacturing Systems, 54:74–93, 2020.

[25] H. M. Wagner. An integer linear-programming model for machine scheduling. Naval Research Logistics Quarterly, 6(2):131–140, 1959.

[26] J. M. Wilson. Alternative formulations of a flow-shop scheduling problem. Journal of the Operational Research Society, 40(4):395–399, 1989.

[27] L. Yu, C. Zhu, J. Shi, and W. Zhang. An extended flexible job shop scheduling model for flight deck scheduling with priority, parallel operations, and sequence flexibility. Scientific Programming, 2017:1–15, 2017.

:::info
Authors:

(1) K. A. G. Araujo, Department of Applied Mathematics, Institute of Mathematics and Statistics, University of Sao Paulo, Rua do Matao, 1010, Cidade Universitaria, 05508-090, Sao Paulo, SP, Brazil ([email protected]);

(2) E. G. Birgin, Department of Computer Science, Institute of Mathematics and Statistics, University of Sao Paulo, Rua do Matao, 1010, Cidade Universitaria, 05508-090, Sao Paulo, SP, Brazil ([email protected]);

(3) D. P. Ronconi, Department of Production Engineering, Polytechnic School, University of Sao Paulo, Av. Prof. Luciano Gualberto, 1380, Cidade Universitaria, 05508-010 Sao Paulo, SP, Brazil ([email protected]).

:::

:::info
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.

:::