Table of Links
Abstract and 1. Introduction
- The Model Set-up
- Price Impact in a Market with No Transaction Costs
- Price Impact in a Market with Transaction Costs
Appendix A. Proofs of Section 3
Appendix B. Proofs of Section 4
References
4. Price Impact in a Market with Transaction Costs
In this section we aim to generalize the concept of the Nash equilibrium under the presence of exogenous market transaction costs. As in the frictionless case, we build our price-impact equilibrium upon the corresponding competitive one. For this, we begin our analysis with a brief introduction on the competitive equilibrium when each investor faces transaction costs upon trading.

4.2. The price impact of a single investor in a market with transaction costs. We return to the concept of price impact imposing now transaction costs to the market. As in the frictionless equilibrium, we first consider the simplified case, where only one investor (say investor n) acts strategically, while the rest stay price-takers. Although there is a characterization of the unique equilibrium in the competitive setting, there is no general explicit formula for the equilibrium returns. This comes in sharp contrast to the frictionless case and makes the determination of the impact of investor n to the equilibrium return (and hence her best-response) quite challenging. However, as we shall show below, the following assumption allows us to go beyond a characterization of the market’s equilibirum returns and deal both with the best-response and the Nash equilibrium under transaction costs.

Assumption 4.2. ζm, ν ∈ H∞ for all m ∈ I and φn, ψ ∈ WA.
When considering the frictional analogue of the price-impact process for investor n introduced in (11), A becomes a natural choice for her control. In other words, by observing how the rest of the investors act optimally as price takers at the equilibrium, we have the following result:

Based on a calculus of variations argument, we get the following result for the frictional best-response strategy of investor n:

The existence and uniqueness of the solution of (26) is stated in the following proposition. In fact, this FBSDE is a part of a larger class of linear FBSDEs that do admit unique (global) solutions.
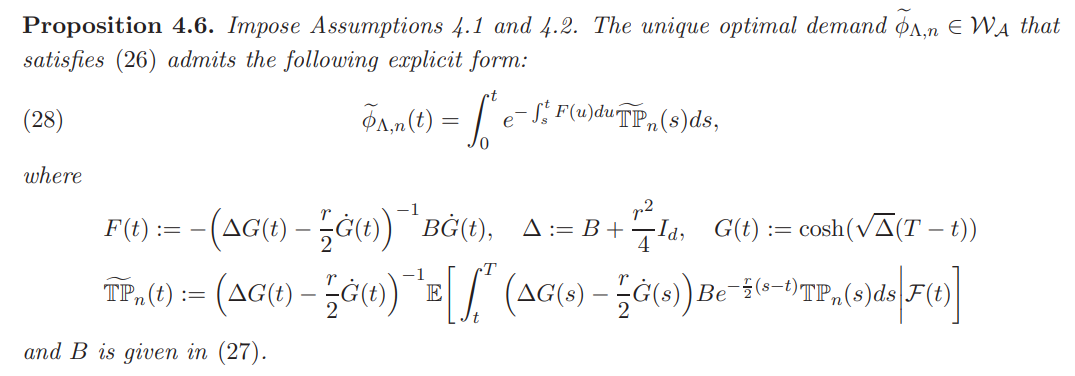
Based on the above characterization, we are able to provide a closed-form expression for the equilibrium returns under transaction costs when only investor n acts strategically and the rest of the investors are price takers.
Corollary 4.7. Impose Assumptions 4.1 and 4.2. In a market with transaction costs, when only investor n acts strategically, the unique equilibrium returns in this context are given by:
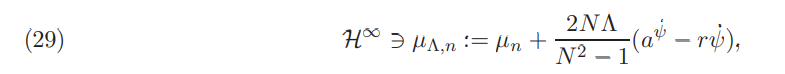
where µn is the corresponding frictionless equilibrium given in (15).
Remark 4.8. A direct consequence of (29) is that equal risk tolerances result in equilibrium returns under single investor’s price impact with transaction costs being equal to the corresponding frictionless equilibrium if there is no noise traders (i.e. no liquidity premium is created). This is in line with the price-taking equilibrium. Indeed, as shown in [BFHMK18], quadratic transaction costs do not change the equilibrium returns as long as there is homogeneous risk aversion and absence of noise traders. This also holds when a single and (as we shall verify below) all investors act strategically. When noise traders are present, positive liquidity premium is created when the rate of noise demand is sufficiently high (or simply positive when r = 0). In fact, comparing (29) to the Corollary 5.4 of [BFHMK18], the strategic behaviour of a single investor increases the equilibrium return (and hence the liquidity premium) with transaction costs. From (29), we also verify that µΛ,n converges to µn (i.e. liquidity premium vanishes) when Λ goes to zero.
4.3. The Nash equilibrium returns in a market with transaction costs. We are now ready to generalize the concepts presented in §3.2 in a market with transaction costs. To this end, we extend Assumption 4.2 to each φm, m ∈ I and begin with a characterization of the investors’ demands when all of them act strategically. More precisely, by shifting the investors’ exposure, in accordance to Definition 3.7, the linear system (18) becomes the following system of linear FBSDEs, under the same boundary value conditions as (26), for m ∈ I:
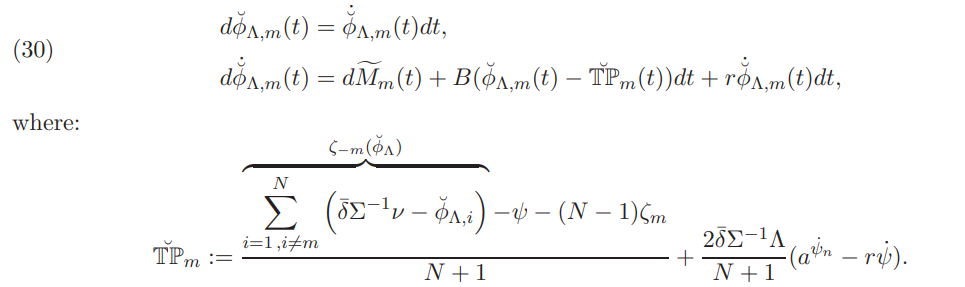
The uniqueness of the Nash equilibrium returns also holds in the market with transaction costs and is a consequence of the following lemma:
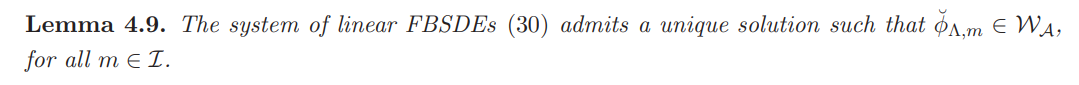
With the above result in hand we are ready to derive the point at which the frictional market equilibrates when all the agents act strategically.
Theorem 4.10. Impose Assumptions 4.1 and 4.2. In a market with transaction costs, the unique Nash equilibrium returns are given by:
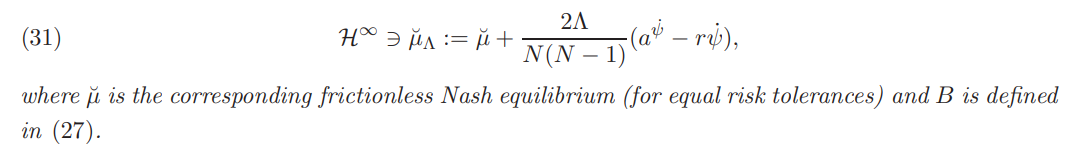
Remark 4.11. Based on Remark 4.8, we expect that the absence of noise traders and equal risk tolerances would result in Nash equilibrium returns with transaction costs being equal to the frictionless competitive ones. Indeed, this stems directly from (31). In fact, under common risk tolerance, we have seen from (20) that the absence of noise traders also implies that the frictionless Nash equilibrium equals to the competitive one too. Furthermore, comparing (31) to the frictional competitive equilibrium returns derived in [BFHMK18], liquidity premium that stems from transaction costs is higher in the non-competitive case if and only if N > 2. In words, when more than two strategic investors with the same risk tolerance participate in the market, the effect of transaction costs on liquidity premium is higher due their strategic behavior. In the special case of only two strategic investors the effect of transaction costs on liquidity premium is equal between competitive and noncompetitive market’s structure. Finally, as expected, when Λ tends to zero, liquidity premium due to transaction costs vanishes.
4.4. The case of two investors. Interestingly, Assumption 4.1 in Theorem 4.10 can be dropped when considering a market of only two investors, i.e. N = 2. In fact even in the case of different risk tolerances a strong connection between the frictional and frictionless Nash equilibrium returns remains. This is supported by the following result:
Theorem 4.12. Impose Assumption 4.2 and let N = 2. In a market with transaction costs, the unique Nash equilibrium returns are given by:

Note that (32) coincides with (31) when δ1 = δ2.
:::info
Authors:
(1) Michail Anthropelos;
(2) Constantinos Stefanakis.
:::
:::info
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
:::