:::info
Authors:
(1) Michail Anthropelos;
(2) Constantinos Stefanakis.
:::
Table of Links
Abstract and 1. Introduction
- The Model Set-up
- Price Impact in a Market with No Transaction Costs
- Price Impact in a Market with Transaction Costs
Appendix A. Proofs of Section 3
Appendix B. Proofs of Section 4
References
Abstract. We consider an Ito-financial market at which the risky assets’ returns are derived endogenously through a market-clearing condition amongst heterogeneous risk-averse investors with quadratic preferences and random endowments. Investors act strategically by taking into account the impact that their orders have on the assets’ drift. A frictionless market and an one with quadratic transaction costs are analysed and compared. In the former, we derive the unique Nash equilibrium at which investors’ demand processes reveal different hedging needs than their true ones, resulting in a deviation of the Nash equilibrium from its competitive counterpart. Under price impact and transaction costs, we characterize the Nash equilibrium through the (unique) solution of a system of FBSDEs and derive its closed-form expression. We furthermore show that under common risk aversion and absence of noise traders, transaction costs do not change the equilibrium returns. On the contrary, when noise traders are present, the effect of transaction costs on equilibrium returns is amplified due to price impact.
1. Introduction
It has been an undeniable fact that in several contemporaneous financial markets there are large institutional investors whose trading strategies impact the assets’ prices (see among others the empirical studies in [KY19] and [HHLT21]). Motivated by the related statistical evidence, a large body of theoretical research on price-impact modelling has been recently developed both in static and dynamic settings (for extended literature reviews on price-impact models we refer to [RY22] and [Web23]).
The majority of the existing models in this area, however, do not take into account a prevalent force in the markets: the exogenous transaction costs. Especially when a market is thin, i.e. when the average trading volume is low, transaction costs bedevil the investors in several forms, such as broker and trading platform’s fees ([FIM18]) and searching-time for counterpart ([DGP05]). Such transaction costs can be seen as an additional type of market’s frictions on top of its noncompetitiveness.
In this paper, we study a continuous-time market populated by strategically behaved investors who exploit their price impact, while being charged with transaction costs on their trading. More precisely, we assume that risky assets follow Itˆo dynamics, with drifts that are endogenously derived at the equilibrium. The presence of noise traders is allowable in the model, while the main market’s participants are mean-variance investors endowed with heterogeneous random income processes. Driven by their hedging needs, investors trade the risky assets and the market-clearing condition determines the equilibrium drift of assets’ return. In contrast to the related literature (see among others [Bas00]), we assume (as in [RW15]) that all investors are strategic, in the sense that each one takes into account her impact to market equilibrium when submitting an order. Unlike [RW15] however, we impose (as in [BFHMK18]) quadratic transaction costs on investors’ trading, which we argue it is a more appropriative market setting for thin financial markets. To the best of our knowledge, this is the first attempt to model a continuous-time market equilibrium with the simultaneous presence of transaction costs and endogenous price impact.
Main contributions. The paper analyses and compares two main market settings: one without transaction costs (also called frictionless) and another with the presence of transaction costs (also called frictional market). We use the frictionless market as a benchmark to highlight the effect of transaction costs on market equilibrium, but also to introduce in a more clear manner the way we model investors’ price impact. For this, we write the market’s equilibrium return as a function of each investor’s demand given that the rest of the investors act optimally (similarly to the static models of [Ant17] and [AK17]). This creates a best-response function which in turn leads to a continuous-time Nash equilibrium for market returns.
We derive these equilibrium returns in closed-form and verify that investors’ price impact does always change the market’s drift when noise traders are present (even under common risk aversion). In fact, at the equilibrium trading, price impact makes the investors reveal different hedging needs than their true ones. In particular, this leads to lower non-competitive equilibrium returns (and hence higher equilibrium prices) when noise traders buy the risky assets (from equally risk tolerant investors). Consistent to the related literature ([MR17] and [AK24]), we also show that Nash equilibrium produces better utility gains for investors with sufficiently low risk aversion, when compared with the associate competitive equilibrium.
We then apply this price-impact concept in a market with quadratic transaction costs. For such extension, we have to deal with a number of challenges. It is well known that equilibrium models with transaction costs are intractable, because trading costs complicate the investors’ individual optimization objectives. In our case, the problem is compounded since there is no general explicit expression of the competitive equilibrium returns in the market, which means that there is no direct way to identify investors’ price impact. For this, we restrict the class of admissible strategies and model’s parameters and assume common risk tolerance, which in turn leads to the (frictional) best-response strategy satisfying an explicitly solvable coupled but linear FBSDE. Building on this, we characterize the investors’ Nash equilibrium demands through an associate system of linear FBSDEs, which admits an explicit solution. We then derive a closed-form expression of the (frictional) Nash equilibrium returns.
The closed-form formulas allow us to compare the market’s return under different types of equilibria in two directions: with and without transaction costs and with and without price impact. The impact on investors’ frictional objectives comes both in their linear and quadratic parts. The linear part exploits solely the direction of noise traders demand, while the quadratic part indicates the negative effect of transaction costs on investor’s strategic behavior. On the other hand, we show that investors’ price impact increases the part of the equilibrium return that stems from transaction costs (when more than two investors participate in the market). In the special case of only two strategic investors, the effect of transaction costs on equilibrium returns is equal between competitive and non-competitive market’s structure. We also highlight the importance of homogeneous risk preference on equilibrium comparison. In particular, when investors have common risk aversion and there is no noise traders in the market, we show that frictional and frictionless Nash equilibrium coincide (a result that holds under competitive market structure too).
Connection with the related literature. Our paper is linked with two strands of the literature: equilibrium models with price impact and the optimal investment and equilibrium pricing under transaction costs.
There different categorisations of price-impact models (with or without time-dynamic setting) regarding the source of price impact and the (a)symmetry of participating investors. On one hand, there is a vast literature that assumes exogenous price impact, e.g. [AC00], [ATHL05], [HW04] and [SZ19]. Therein, specific assumptions are used to justify the nature of the price impact that could be permanent or temporary. In contrast to this approach, we follow the literature that starts from the seminal work of [Kyl85] and considers an endogenously derived price impact. In fact, similarly to the static models of [Ant17], [Viv11] and [MR17] and the time-dynamic ones in [Vay99] and [RW15], all investors, except the noise ones, have symmetric bargaining power and internalize their ability to affect the equilibrium returns.
There are two main advantages of imposing endogenous price impact: the first is that there is no need to impose an exogenous parametrization of impact and second that we can analyse the equilibrium price impact in terms of investors’ characteristics such as their risk exposures, risk preferences and/or even their population.
Our work contributes also on equilibrium market models with transaction costs incorporating a non-competitive market structure. Under that perspective, we extend the equilibrium models of [BFHMK18] and [HMKP21] and show that price-impact not only can be taken into account, but also the equilibrium outcomes can be analytically and qualitatively compared. Equilibrium models with dynamic trading and transaction costs, however without assuming price-impact, have been developed both in discrete-time setting (e.g. [BD19]) and under continuous-time (e.g. [Vay98]). Equilibrium continuous-time models with transaction costs are also developed in [VV99] and [Wes18], but under simplified settings with deterministic asset prices.
On the other hand, Nash equilibria under price impact and transaction costs in an dynamic setting have studied in [SZ19] and [LS19] and more recently extended in [CL24], under the notion of price impact game. In contrast to our setting, these works consider exogenous price impact, while the trading occurs in discrete times.
Structure of the paper. This paper is organized as follows: Section 2 presents the model’s ingredients and the simple case of the competitive equilibrium with no transaction costs. In Section 3, we introduce the price impact modelling in a frictionless market, derive the closed-form expression of the Nash equilibrium returns and comment on its intuition. In Section 4, we generalize the model by including quadratic transaction costs and solve the system of FBSDEs that characterizes the corresponding Nash equilibrium returns. Finally, in Appendix A we provide the proofs of Section 3, while the proofs of Section 4 are given in Appendix B.
2. The Model Set-up

Remark 2.1. Considering only the diffusion part of the investors’ random endowment in (3) comes without loss of generality. Indeed, as stated in [HMKP21], since the solution to the investors’ objective functional (see (5) below) is invariant to any additional finite variation part or to endowment’s shocks that are orthogonal to the market. In other words, under suitable integrability assumptions, (3) could be generalized to:

and impose the following standing assumption:
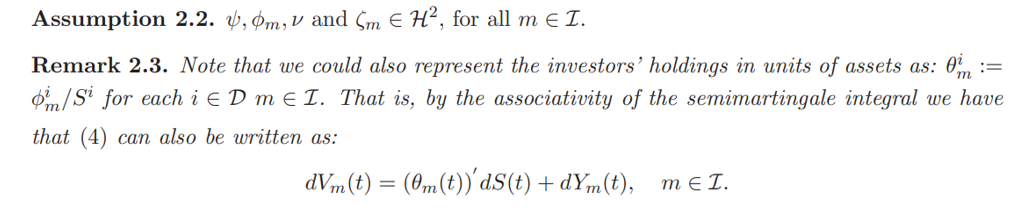


The above investment strategy shall be called the competitive frictionless optimal portfolio of investor m. Note that the first term of (6) is the classic quadratic optimal portfolio (also called Merton’s portfolio), while the second reflects the investor’s hedging needs.
Under competitive market structure with no transaction costs, the local return process ν of (1) is determined simply by the market-clearing condition, where a zero-net supply is imposed:
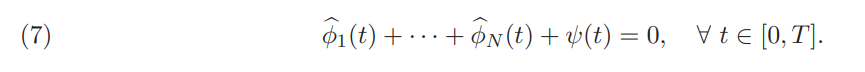
Without transaction costs and when all investors are price takers, we readily get from (6) and (7), the explicit form for the equilibrium return process, henceforth called frictionless competitive equilibrium returns:

where the aggregate investors’ risk exposure and risk tolerance are defined as:
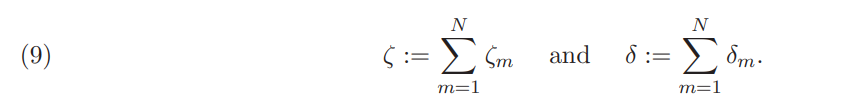
Due to Assumption 2.2, we directly verify that µ ∈ H2 . Equilibrium (8) is indicative for the discussion that follows. Say d = 1, for simplicity. Assuming that the aggregate investors’ exposure to market shocks is higher than the corresponding noise demand, the equilibrium returns increase when aggregate risk tolerance decreases and the asset’s volatility increases. This is intuitive: lower risk tolerance and higher risk means that investors decrease their demand for the asset and hence equilibrium returns increase. Note that higher equilibrium returns essentially imply that investors require higher expected returns in order to invest on the asset, a situation that is consistent to lower demand. On the other hand, higher exposure to market shocks increases investors’ demand and hence decreases the required expected returns at the equilibrium.
:::info
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
:::