Table of Links
I. Introduction
II. Theoretical Aspects
III. Experimental Setup
IV. Results and Discussion
V. Conclusion and References
Quantum random number generation (QRNG) is a resource that is a necessity in the field of cryptography. However, its certification has been challenging. In this article, we certify randomness with the aid of quantum entanglement in a device independent setting, where we choose two-photon interference for source characterisation. The CHSH inequality violation and quantum state tomography are used as independent checks on the measurement devices. These measures ensure the unpredictability of quantum random number generation. This work can be easily extended to faster randomness expansion protocols.
I. INTRODUCTION
Random numbers are a pre-requisite for many cryptographic applications as proposed by Claude Shannon in 1948 [1]. This requirement is typically fulfilled by use of algorithmically generated random bit stream, also referred to as pseudo random number generators (PRNGs). PRNGs have many applications ranging from digital signatures to IoT applications [2]. On the other front, military grade applications require highly secure random number generators. Quality of randomness in PRNGs relies on their computational complexity and their length. [3]. However, they can turn obsolete in cryptographic applications pertaining to advance algorithms which can dig up the low computational resolution making the apparently random bit streams, non-random. Quantum random number generators (QRNGs) provide an alternative based on their quantum unpredictability (arising from laws of quantum mechanics) [4]. Many types of QRNGs have been studied both in discrete [5] and continuous [6] degrees of freedom for their use in cryptographic applications.
On the testing front, NIST Statistical Test Suite, Dieharder [7], ENT [8] have been used to prove randomness of QRNGs. But this is half-baked truth. NIST Statistical Test Suite [9], as the name suggests, are used for testing statistical properties like uniformity amongst PRNGs and thus, can strictly be used to check for statistical properties of QRNGs. To check for the unpredictability of PRNGs, NIST has provided a test suite based on entropy model [10]. Nonetheless for the quantum case, one has to use some quantum correlation quantifier like quantum entanglement measures [11]. For example, given n bits, these quantum correlations forbid one to predict (n+1)th bit. There is no common consensus on using a single quantum certification for all quantum random number generators and hence, different works in the literature use different techniques for certification [12]. By certification, we understand that a given quantifier can certify that the bits generated have a quantum correlation. This work uses quantum measures like CHSH inequality violation [13] as a quantifier.
On the device independence front, treating the process of generation and measurement as a black box requires a lot of independent checks and thus, resources. Our technique, being device-independent, assumes no constraints imposed by the devices. Such a technique can easily be integrated into faster device-independent protocols [14, 15] by using an efficient non-linear crystal.
The article is subdivided into following four sections. Section II discusses about the theoretical framework required to understand the physical process of generation and certification of random number generation. Section III describes the experimental setup on how to generate random numbers from bipartite quantum entanglement. Section IV discusses the random bits generated in a device independent manner. It discusses their performance against standard tests. Section V draws conclusions on different aspects of this study.
II. THEORETICAL ASPECTS
Before discussing the experimental setup, we need to understand the theoretical framework which circumscribes the quantum random number generation and testing process. First, we discuss the generation process of QRNG and discuss it’s source-independence. Next, we discuss the typical method (NIST Statistical Test Suite) of checking uniformity of QRNGs. Thirdly, we describe the quantifiers from quantum mechanics for certification of unpredictability of QRNGs.
A. Generating random numbers from quantum entanglement
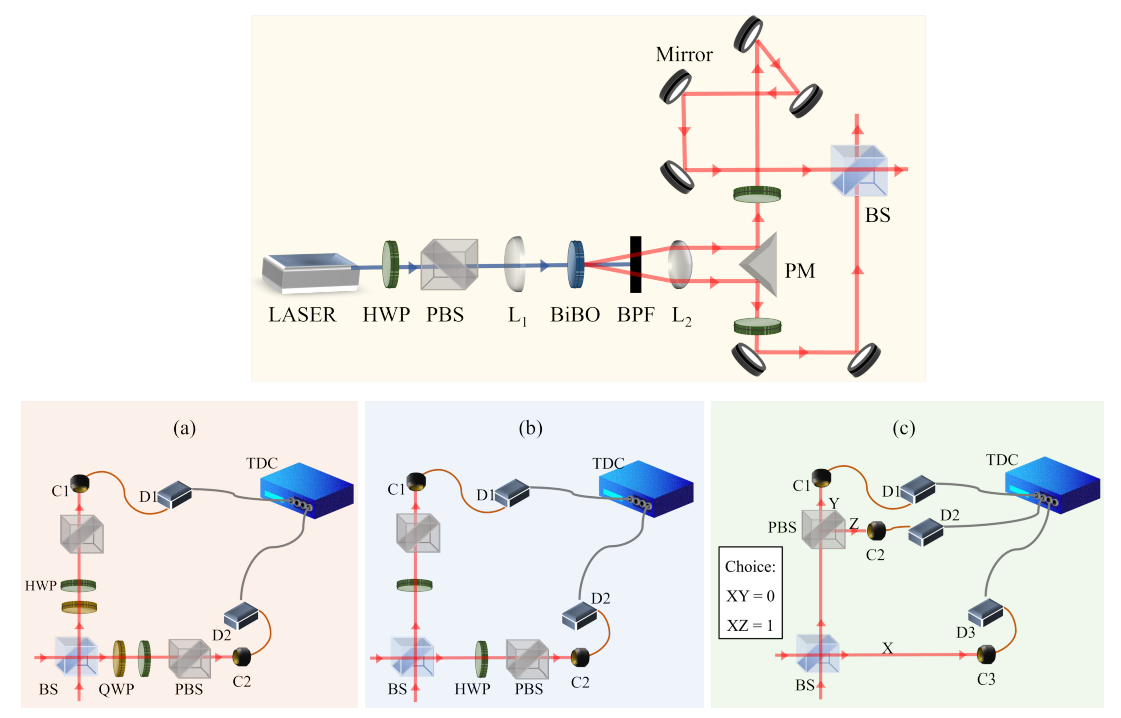
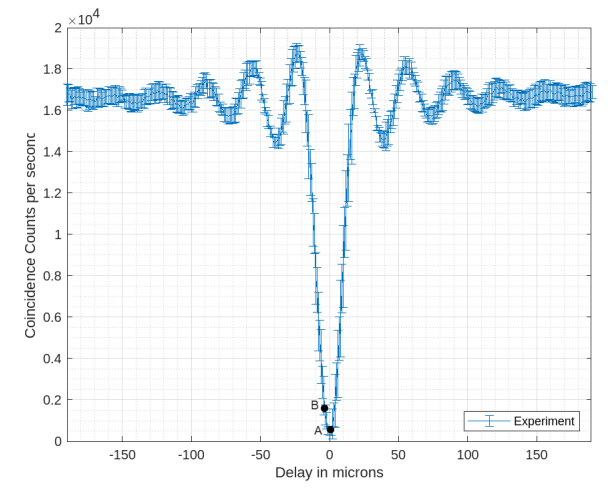
The use of quantum entanglement for the generation of quantum random numbers, requires the ability to verifiably produce high quality entangled states. For this, we use a quantum eraser experimental setup derived from Hong Ou Mandel (HOM) interference. Once at the dip point of the HOM interference curve, we can generate entangled photons by making the photons distinguishable in one degree of freedom, say polarization analogous to the quantum eraser experiment as described in [16]. This is done by rotating one of the half waveplates by 45°. Theoretically, the output state of Hong Ou Mandel (represented by pt. A in Fig. 2) is
If the polarisation of one of the photon is rotated by 45 ° to the horizontal, the state transforms to
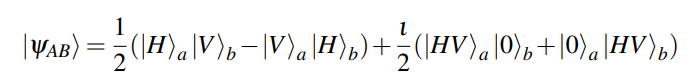
Because our detectors are click detectors, the post-selected state reduces to Eq. 1. Finally, we generate random numbers through a bipartite entangled state. Mathematically, a maximally entangled state in polarisation can be written as

B. NIST Statistical Test Suite
The NIST Statistical Test Suite is a hypothesis based suite which checks whether a given sequence is random. The teststatic p gives the confidence level in the hypothesis with a threshold set to 0.01. The test suite entails 15 tests with numerous sub-tests. These tests check for patterns in the bitstream in long as well as short range. The tests include autocorrelation, compression and spectral frequency-based tests [9]. In other words, they check for uniformity of the bit stream. Before testing against NIST test suite, the data is post-processed using Toeplitz hash function. The advantage of using Toeplitz hash function is that it scrambles the ”quantum information” evenly amongst all bits. This is ensured by 2-universality of Toeplitz hash function [18].
C. Theoretical framework to study Quantum Entanglement
Several authors [19] have provided methods to quantify “entanglement” as a resource with the aid of different measures [11, 20–22]. One of the well studied experimental entanglement measure is CHSH inequality [23]. The CHSH inequality measures correlations between two qubits using different measurement bases. For an entangled pair A and B, we will label the bases for the qubit A to be a, a′, and for qubit B to be b, b ′ respectively. This allows us to calculate the CHSH parameter S,
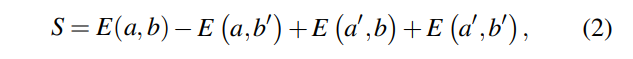
where, E(a,b), represents the expectation value of the product of measurements in a-b basis. The same holds true for other combinations of a′ -b′ basis. For CHSH parameter S ≥ 2, the measured state shows quantum entanglement.

. Consider a 2-qubit state characterized by its density matrix ρ, which can be written as follo

Bayesian quantum state estimation
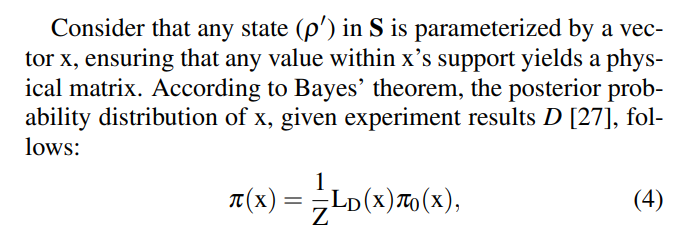

Maximum likelihood quantum state estimation

:::info
Authors:
(1) Vardaan Mongia, Quantum Science and Technology Laboratory, Physical Research Laboratory, Ahmedabad, 380009, India and Dept. of Physics, Indian Institute of Technology Gandhinagar, Gujarat, 382355, India;
(2) Abhishek Kumar, Space Weather Laboratory, Physical Research Laboratory, Ahmedabad, 380009, India;
(3) Shashi Prabhakar, Quantum Science and Technology Laboratory, Physical Research Laboratory, Ahmedabad, 380009, India;
(4) Anindya Banerji, Center for Quantum Technologies, National University of Singapore, Singapore 117543;
(5) R.P. Singh, Quantum Science and Technology Laboratory, Physical Research Laboratory, Ahmedabad, 380009, India.
:::
:::info
This paper is available on arxiv under CC BY 4.0 DEED license.
:::