Table of Links
Abstract and 1. Introduction
-
Dynamic Inverse Problems in Imaging
2.1 Motion Model
2.2 Joint Image Reconstruction and Motion Estimation
-
Methods
3.1 Numerical evaluation with Neural Fields
3.2 Numerical evaluation with grid-based representation
-
Numerical Experiments
4.1 Synthetic experiments
-
Conclusion, Acknowledgments, and References
4 Numerical Experiments
4.1 Synthetic experiments

4.1.1 Two-squares phantom

Remark 1 The second row in figure 1 represents the velocity field as follows: the coloured boundary frame indicates the direction of the velocity field. The intensities of the image indicate the magnitude of the vector. As an example, the square on the right moves constantly up and slightly to the right during the motion.
Measurements are obtained by sampling one random angle per frame and further corrupted with Gaussian noise with standard deviation σ = 0.01. See the third row in figure 1. To highlight the necessity of motion models, two naive reconstructions are shown in the fourth row of figure 1. The one on the left corresponds to a time-static reconstruction, i.e., assuming that the squares are not moving. The result is an image that blurs those regions where the squares moved. The one on the right is a frame-by-frame reconstruction which, as expected, cannot get a reliable reconstruction from one projection only.
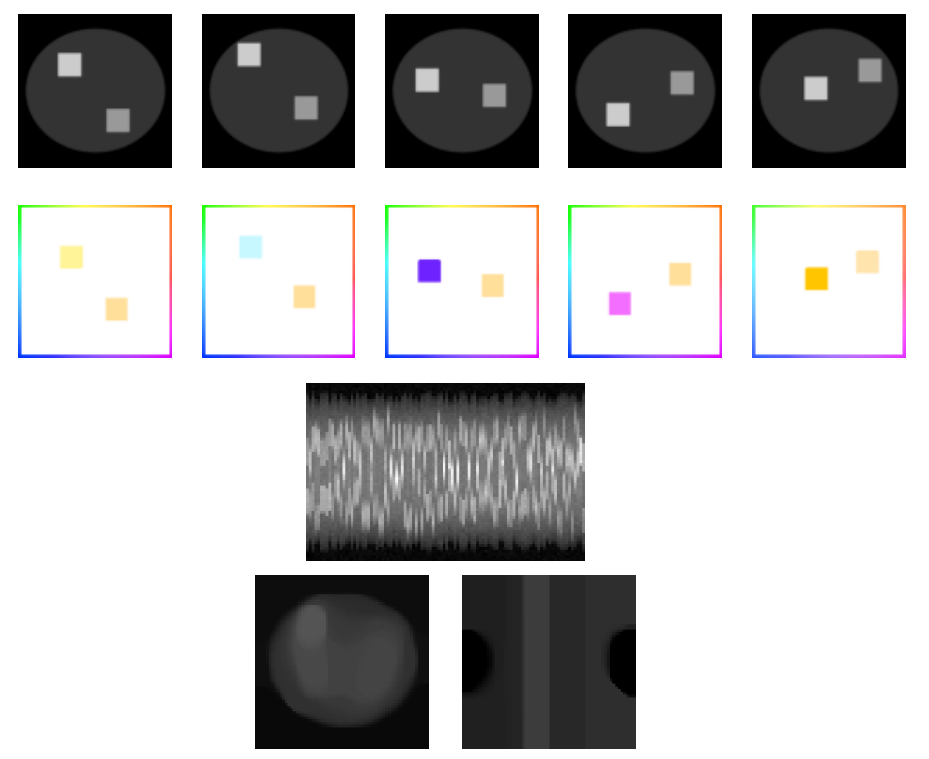
Effect of the motion regularization parameter γ.

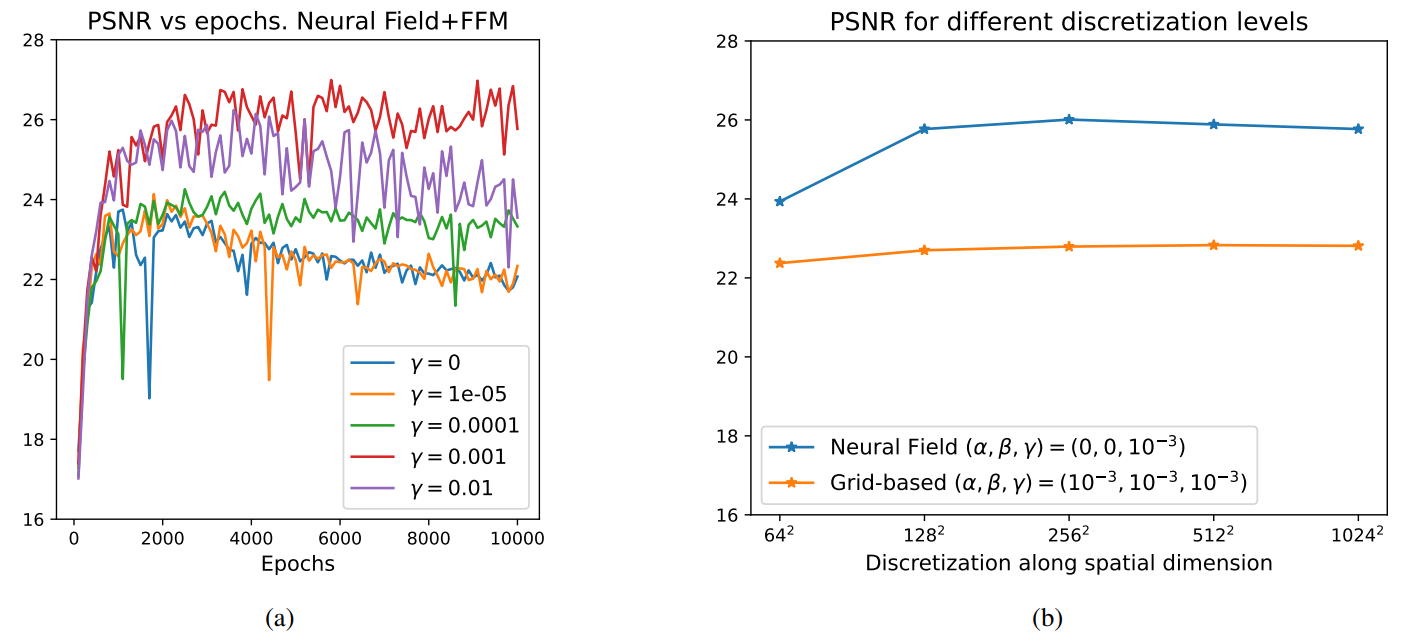
Neural fields versus Grid-based method.
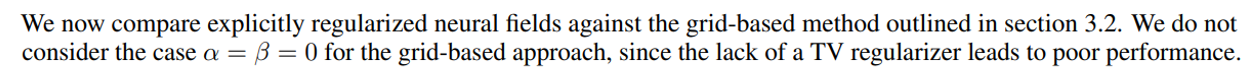

Generalization into higher resolution.


5 Conclusion
In this work we studied neural fields for dynamic inverse problems. We saw how to enhance neural fields reconstruction for dynamic inverse problems by making use of explicit PDE-based motion regularizers, namely, the optical flow equation. Constraining the neural field to this physically feasible motion meant a significant improvement with respect to the more widely used motionless implicitly regularized network. This opens the option for studying more motion models, e.g., continuity equation for 3D+time problems, for neural fields since most of the literature relies entirely on the implicit regularization of the network. We saw that the motion regularization parameter γ played a relevant role in the quality of the reconstruction however its choice is not clear, a small value of it led to a similar behaviour with the implicitly regularized neural field, while a very large value promotes no motion. Finally, we highlight that our goal was to improve the reconstruction of the image leaving the motion estimation as an auxiliary problem and not a goal.

However, there are applications where the motion is a relevant quantity, for example it is used in cardiac imaging for clinical assessment of the heart. In such cases, it can be necessary to think of explicit regularizers for the motion as well.
We have also studied the performance of neural fields against classical grid-based representations, in this case, an alternating scheme plus PDHG, and even for the choice of regularization parameters α, β, γ for which this approach performed the best, neural fields still were better in terms of PSNR.
We conclude that neural fields with explicit regularizers can significantly improve the discovery of spatiotemporal quantities. Their mesh-free nature makes them suitable for such tasks since derivatives can be computed via automatic differentiation but also their memory consumption can remain controlled even for large-scale imaging tasks [33].
Acknowledgments
Pablo Arratia is supported by a scholarship from the EPSRC Centre for Doctoral Training in Statistical Applied Mathematics at Bath (SAMBa), under the project EP/S022945/1.
References
[1] Jennifer A Steeden, Grzegorz T Kowalik, Oliver Tann, Marina Hughes, Kristian H Mortensen, and Vivek Muthurangu. Real-time assessment of right and left ventricular volumes and function in children using high spatiotemporal resolution spiral bssfp with compressed sensing. Journal of Cardiovascular Magnetic Resonance, 20(1):79, 2018.
[2] Tatiana A Bubba, Maximilian März, Zenith Purisha, Matti Lassas, and Samuli Siltanen. Shearlet-based regularization in sparse dynamic tomography. In Wavelets and Sparsity XVII, volume 10394, pages 236–245. SPIE, 2017.
[3] Esa Niemi, Matti Lassas, Aki Kallonen, Lauri Harhanen, Keijo Hämäläinen, and Samuli Siltanen. Dynamic multisource x-ray tomography using a spacetime level set method. Journal of Computational Physics, 291:218–237, 2015.
[4] Martin Burger, Hendrik Dirks, and Carola-Bibiane Schönlieb. A variational model for joint motion estimation and image reconstruction, Jan 2018.
[5] Martin Burger, Jan Modersitzki, and Sebastian Suhr. A nonlinear variational approach to motion-corrected reconstruction of density images. arXiv preprint arXiv:1511.09048, 2015.
[6] Martin Burger, Hendrik Dirks, Lena Frerking, Andreas Hauptmann, Tapio Helin, and Samuli Siltanen. A variational reconstruction method for undersampled dynamic x-ray tomography based on physical motion models. Inverse Problems, 33(12):124008, 2017.
[7] Angelica I Aviles-Rivero, Noémie Debroux, Guy Williams, Martin J Graves, and Carola-Bibiane Schönlieb. Compressed sensing plus motion (cs+ m): a new perspective for improving undersampled mr image reconstruction. Medical Image Analysis, 68:101933, 2021.
[8] Andreas Hauptmann, Ozan Öktem, and Carola Schönlieb. Image reconstruction in dynamic inverse problems with temporal models. Handbook of Mathematical Models and Algorithms in Computer Vision and Imaging: Mathematical Imaging and Vision, pages 1–31, 2021.
[9] Yiheng Xie, Towaki Takikawa, Shunsuke Saito, Or Litany, Shiqin Yan, Numair Khan, Federico Tombari, James Tompkin, Vincent sitzmann, and Srinath Sridhar. Neural fields in visual computing and beyond, May 2022.
[10] Vincent Sitzmann, Julien Martel, Alexander Bergman, David Lindell, and Gordon Wetzstein. Implicit neural representations with periodic activation functions. Advances in Neural Information Processing Systems, 33:7462– 7473, 2020.
[11] M. Raissi, P. Perdikaris, and G.E. Karniadakis. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378:686–707, Feb 2019.
[12] Salvatore Cuomo, Vincenzo Schiano Di Cola, Fabio Giampaolo, Gianluigi Rozza, Maizar Raissi, and Francesco Piccialli. Scientific machine learning through physics-informed neural networks: Where we are and what’s next. arXiv preprint arXiv:2201.05624, 2022.
[13] Guangming Zang, Ramzi Idoughi, Rui Li, Peter Wonka, and Wolfgang Heidrich. Intratomo: self-supervised learning-based tomography via sinogram synthesis and prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 1960–1970, 2021.
[14] Yu Sun, Jiaming Liu, Mingyang Xie, Brendt Wohlberg, and Ulugbek S Kamilov. Coil: Coordinate-based internal learning for imaging inverse problems. arXiv preprint arXiv:2102.05181, 2021.
[15] Albert W Reed, Hyojin Kim, Rushil Anirudh, K Aditya Mohan, Kyle Champley, Jingu Kang, and Suren Jayasuriya. Dynamic ct reconstruction from limited views with implicit neural representations and parametric motion fields. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 2258–2268, 2021.
[16] Junshen Xu, Daniel Moyer, Borjan Gagoski, Juan Eugenio Iglesias, P Ellen Grant, Polina Golland, and Elfar Adalsteinsson. Nesvor: Implicit neural representation for slice-to-volume reconstruction in mri. IEEE Transactions on Medical Imaging, 2023.
[17] Johannes F Kunz, Stefan Ruschke, and Reinhard Heckel. Implicit neural networks with fourier-feature inputs for free-breathing cardiac mri reconstruction. arXiv preprint arXiv:2305.06822, 2023.
[18] Wenqi Huang, Hongwei Bran Li, Jiazhen Pan, Gastao Cruz, Daniel Rueckert, and Kerstin Hammernik. Neural implicit k-space for binning-free non-cartesian cardiac mr imaging. In International Conference on Information Processing in Medical Imaging, pages 548–560. Springer, 2023.
[19] Jie Feng, Ruimin Feng, Qing Wu, Zhiyong Zhang, Yuyao Zhang, and Hongjiang Wei. Spatiotemporal implicit neural representation for unsupervised dynamic mri reconstruction. arXiv preprint arXiv:2301.00127, 2022.
[20] Tabita Catalán, Matías Courdurier, Axel Osses, René Botnar, Francisco Sahli Costabal, and Claudia Prieto. Unsupervised reconstruction of accelerated cardiac cine mri using neural fields. arXiv preprint arXiv:2307.14363, 2023.
[21] Jelmer M Wolterink, Jesse C Zwienenberg, and Christoph Brune. Implicit neural representations for deformable image registration. In International Conference on Medical Imaging with Deep Learning, pages 1349–1359. PMLR, 2022.
[22] Pablo Arratia López, Hernán Mella, Sergio Uribe, Daniel E Hurtado, and Francisco Sahli Costabal. Warppinn: Cine-mr image registration with physics-informed neural networks. Medical Image Analysis, 89:102925, 2023.
[23] Jing Zou, Noémie Debroux, Lihao Liu, Jing Qin, Carola-Bibiane Schönlieb, and Angelica I Aviles-Rivero. Homeomorphic image registration via conformal-invariant hyperelastic regularisation. arXiv preprint arXiv:2303.08113, 2023.
[24] Dieuwertje Alblas, Christoph Brune, Kak Khee Yeung, and Jelmer M Wolterink. Going off-grid: continuous implicit neural representations for 3d vascular modeling. In International Workshop on Statistical Atlases and Computational Models of the Heart, pages 79–90. Springer, 2022.
[25] Ben Mildenhall, Pratul P Srinivasan, Matthew Tancik, Jonathan T Barron, Ravi Ramamoorthi, and Ren Ng. Nerf: Representing scenes as neural radiance fields for view synthesis. Communications of the ACM, 65(1):99–106, 2021.
[26] Kurt Hornik, Maxwell Stinchcombe, and Halbert White. Multilayer feedforward networks are universal approximators, Jan 1989.
[27] Martin Hutzenthaler, Arnulf Jentzen, Thomas Kruse, and Tuan Anh Nguyen. A proof that rectified deep neural networks overcome the curse of dimensionality in the numerical approximation of semilinear heat equations. SN partial differential equations and applications, 1(2):10, 2020.
[28] Arnulf Jentzen, Diyora Salimova, and Timo Welti. A proof that deep artificial neural networks overcome the curse of dimensionality in the numerical approximation of kolmogorov partial differential equations with constant diffusion and nonlinear drift coefficients. arXiv preprint arXiv:1809.07321, 2018.
[29] Nasim Rahaman, Aristide Baratin, Devansh Arpit, Felix Draxler, Min Lin, Fred Hamprecht, Yoshua Bengio, and Aaron Courville. On the spectral bias of neural networks. In International conference on machine learning, pages 5301–5310. PMLR, 2019.
[30] Arthur Jacot, Franck Gabriel, and Clément Hongler. Neural tangent kernel: Convergence and generalization in neural networks. Advances in neural information processing systems, 31, 2018.
[31] Sifan Wang, Hanwen Wang, and Paris Perdikaris. On the eigenvector bias of fourier feature networks: From regression to solving multi-scale pdes with physics-informed neural networks. Computer Methods in Applied Mechanics and Engineering, 384:113938, 2021.
[32] Matthew Tancik, Pratul Srinivasan, Ben Mildenhall, Sara Fridovich-Keil, Nithin Raghavan, Utkarsh Singhal, Ravi Ramamoorthi, Jonathan Barron, and Ren Ng. Fourier features let networks learn high frequency functions in low dimensional domains. Advances in neural information processing systems, 33:7537–7547, 2020.
[33] Luke Lozenski, Mark A Anastasio, and Umberto Villa. A memory-efficient dynamic image reconstruction method using neural fields. arXiv preprint arXiv:2205.05585, 2022.
[34] Luke Lozenski, Refik Mert Cam, Mark A Anastasio, and Umberto Villa. Proxnf: Neural field proximal training for high-resolution 4d dynamic image reconstruction. arXiv preprint arXiv:2403.03860, 2024.
[35] Leonid I. Rudin, Stanley Osher, and Emad Fatemi. Nonlinear total variation based noise removal algorithms, Nov 1992. [36] Berthold K.P. Horn and Brian G. Schunck. Determining optical flow, Aug 1981.
[37] Gilles Aubert, Rachid Deriche, and Pierre Kornprobst. Computing optical flow via variational techniques. SIAM Journal on Applied Mathematics, 60(1):156–182, 1999.
[38] Christopher Zach, Thomas Pock, and Horst Bischof. A duality based approach for realtime tv-l 1 optical flow. In Pattern Recognition: 29th DAGM Symposium, Heidelberg, Germany, September 12-14, 2007. Proceedings 29, pages 214–223. Springer, 2007.
[39] Nargiza Djurabekova, Andrew Goldberg, Andreas Hauptmann, David Hawkes, Guy Long, Felix Lucka, and Marta Betcke. Application of proximal alternating linearized minimization (palm) and inertial palm to dynamic 3d ct. In 15th international meeting on fully three-dimensional image reconstruction in radiology and nuclear medicine, volume 11072, pages 30–34. SPIE, 2019.
[40] Felix Lucka, Nam Huynh, Marta Betcke, Edward Zhang, Paul Beard, Ben Cox, and Simon Arridge. Enhancing compressed sensing 4d photoacoustic tomography by simultaneous motion estimation. SIAM Journal on Imaging Sciences, 11(4):2224–2253, 2018.
[41] Michael Stein. Large sample properties of simulations using latin hypercube sampling. Technometrics, 29(2):143– 151, 1987.
[42] Antonin Chambolle and Thomas Pock. A first-order primal-dual algorithm for convex problems with applications to imaging, Dec 2010.
[43] Allard Hendriksen, Dirk Schut, Willem Jan Palenstijn, Nicola Viganò, Jisoo Kim, Daniël Pelt, Tristan van Leeuwen, and K. Joost Batenburg. Tomosipo: Fast, flexible, and convenient 3D tomography for complex scanning geometries in Python. Optics Express, Oct 2021.
[44] Wim Van Aarle, Willem Jan Palenstijn, Jan De Beenhouwer, Thomas Altantzis, Sara Bals, K Joost Batenburg, and Jan Sijbers. The astra toolbox: A platform for advanced algorithm development in electron tomography. Ultramicroscopy, 157:35–47, 2015.
[45] Wim Van Aarle, Willem Jan Palenstijn, Jeroen Cant, Eline Janssens, Folkert Bleichrodt, Andrei Dabravolski, Jan De Beenhouwer, K Joost Batenburg, and Jan Sijbers. Fast and flexible x-ray tomography using the astra toolbox. Optics express, 24(22):25129–25147, 2016.
:::info
Authors:
(1) Pablo Arratia, University of Bath, Bath, UK ([email protected]);
(2) Matthias Ehrhardt, University of Bath, Bath, UK ([email protected]);
(3) Lisa Kreusser, University of Bath, Bath, UK ([email protected]).
:::
:::info
This paper is available on arxiv under CC BY 4.0 DEED license.
:::









