Table Of Links
ABSTRACT
1 INTRODUCTION
2 FLATTENING AND ARC APPROXIMATION OF CURVES
3 EULER SPIRALS AND THEIR PARALLEL CURVES
4 FLATTENED PARALLEL CURVES
5 ERROR METRICS FOR APPROXIMATION BY ARCS
6 EVOLUTES
7 CONVERSION FROM CUBIC BÉZIERS TO EULER SPIRALS
8 GPU IMPLEMENTATION
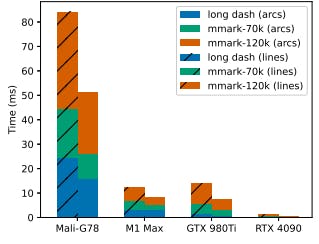
9 RESULTS
CONCLUSIONS, FUTURE WORK AND REFERENCES
10 CONCLUSIONS
Path stroking has received attention in recent years, with Nehab [2020] and Kilgard [2020b] both having proposed a complete theory of correct stroking in vector graphics. While there are a number of implementations of path filling on the GPU, the goal of also implementing stroke expansion on the GPU had not yet been realized. Building upon the theory proposed by Nehab [2020], we implemented an approach to stroke expansion that is GPU-friendly, and achieves high performance on commodity hardware.
We present the Euler spiral as an intermediate representation for a fast and precise approximation of both filled and stroked Bézier paths. Our method for lowering to both line and arc primitives avoids recursion and minimizes divergence, potentially serious problems for parallel evaluation on the GPU.
We propose a novel error metric to directly estimate approximation error as opposed to the commonly employed cut-then-measure approaches which often consume the lion’s share of computational expense. Our approach includes an efficient encoding scheme that alleviates the need for expensive CPU pre-computations and unlocks fully GPU-driven rendering of the entire vector graphics model.
FUTURE WORK
• The GPU implementation sequentializes some work that could be parallel, and is thus not as well load-balanced as it might be. An appealing future direction is to split the pipeline into separate stages, executed by the GPU as nodes in a work graph [21]. This structure is appealing because load balancing is done by hardware.
• The pre-allocation requirement for bump-allocated line soup buffer is a limitation due to today’s graphics APIs. A more accurate and optimized buffer size estimation heuristic is considered future work. It may also be interesting to explore whether graphics APIs can be extended to facilitate GPU-driven scheduling of the compute workload under a bounded memory footprint.
• Many of the error metrics were empirically determined. The mathematical theory behind them should be developed more rigorously, and that process will likely uncover opportunities to fine-tune the technique.
• As mentioned earlier, we did not have time to sufficiently explore a pipeline architecture for GPU-based dashing. Given its parameterization by arc length, we believe the Euler spiral representation lends itself well to an approach based on parallel prefix sums of segment arc lengths.
REFERENCES
[1] 2021. MotionMark 1.2. https://browserbench.org/MotionMark1.2/about.html
[2] World Wide Web Consortium 2024. WebGPU. World Wide Web Consortium. https://www.w3.org/TR/webgpu
[3] Dale Connor and Lilia Krivodonova. 2014. Interpolation of two-dimensional curves with Euler spirals. J. Comput. Appl. Math. 261 (2014), 320–332. https: //doi.org/10.1016/j.cam.2013.11.009
[4] R. T. Farouki and C. A. Neff. 1990. Algebraic properties of plane offset curves. Comput. Aided Geom. Des. 7, 1–4 (jun 1990), 101–127. https://doi.org/10.1016/ 0167-8396(90)90024-L
[5] Francisco Ganacim, Rodolfo S. Lima, Luiz Henrique de Figueiredo, and Diego Nehab. 2014. Massively-parallel vector graphics. ACM Transactions on Graphics 33, 6 (2014), 1–14. https://doi.org/10.1145/2661229.2661274
[6] The gfx-rs authors. 2024. gfx-rs/wgpu. https://github.com/gfx-rs/wgpu
[7] Ron Goldman. 2003. Chapter 5 – Bezier Approximation and Pascal’s Triangle. In Pyramid Algorithms, Ron Goldman (Ed.). Morgan Kaufmann, San Francisco, 187–306. https://doi.org/10.1016/B978-155860354-7/50006-4
[8] Google. 2024. Skia. https://skia.org
[9] Rive Inc. 2024. Rive Renderer. https://github.com/rive-app/ri
[10] Adobe Systems Incorporated. 2008. Document management – Portable document format – Part 1: PDF 1.7. https://opensource.adobe.com/dc-acrobat-sdk-docs/ pdfstandards/PDF32000_2008.pdf
[11] Mark J. Kilgard. 2020. Anecdotal Survey of Variations in Path Stroking among Real-world Implementations. arXiv:2007.12254
[12] Mark J. Kilgard. 2020. Polar Stroking: New Theory and Methods for Stroking Paths. ACM Trans. Graph. 39, 4, Article 145 (Aug. 2020), 15 pages. https: //doi.org/10.1145/3386569.3392458
[13] Benjamin B. Kimia, Ilana Frankel, and Ana-Maria Popescu. 2003. Euler Spiral for Shape Completion. International Journal of Computer Vision 54, 1 (01 Aug 2003), 159–182. https://doi.org/10.1023/A:1023713602895
[14] Samuli Laine and Tero Karras. 2011. High-Performance Software Rasterization on GPUs. HPG ’11: Proceedings of the ACM SIGGRAPH Symposium on High Performance Graphics (2011), 79–88. https://doi.org/10.1145/2018323.2018337
[15] Raph Levien. 2021. Cleaner parallel curves with Euler spirals. https://raphlinus. github.io/curves/2021/02/19/parallel-curves.html
[16] Georg Maier. 2014. Optimal arc spline approximation. Computer Aided Geometric Design 31, 5 (2014), 211–226. https://doi.org/10.1016/j.cagd.2014.02.011
[17] D. S. Meek and D. J. Walton. 2004. An arc spline approximation to a clothoid. J. Comput. Appl. Math. 170, 1 (2004), 59–77. https://doi.org/10.1016/j.cam.2003.12. 038
[18] Smita Narayan. 2014. Approximating Cornu spirals by arc splines. J. Comput. Appl. Math. 255, 1 (2014). https://doi.org/10.1016/j.cam.2013.06.038
[19] Diego Nehab. 2020. Converting Stroked Primitives to Filled Primitives. ACM Trans. Graph. 39, 4, Article 137 (Aug. 2020), 17 pages. https://doi.org/10.1145/ 3386569.3392392
[20] Taweechai Nuntawisuttiwong and Natasha Dejdumrong. 2021. An Approximation of Bézier Curves by a Sequence of Circular Arcs. Information Technology and Control 50, 2 (2021). https://doi.org/10.5755/j01.itc.50.2.25178
[21] Amar Patel and Tex Riddell. 2024. D3D12 Work Graphs. DirectX Developer Blog. https://devblogs.microsoft.com/directx/d3d12-work-graphs/
[22] Ulrich Reif and Andreas Weinmann. 2021. Clothoid fitting and geometric Hermite subdivision. Advances in Computational Mathematics 47, 50 (26 June 2021). https://doi.org/10.1007/s10444-021-09876-5
[23] W. Tiller and E. G. Hanson. 1984. Offsets of two-dimensional profiles. IEEE Computer Graphics and Applications 4, 9 (Sept. 1984), 36–46.
[24] D. J. Walton and D. S. Meek. 2009. G1 interpolation with a single Cornu spiral segment. J. Comput. Appl. Math. 223, 1 (2009), 86–96. https://doi.org/10.1016/j. cam.2007.12.022
[25] Heinrich Wieleitner. 1907. Die Parallelkurve der Klothoide. Archiv der Mathematik und Physik 11 (1907), 373–375.
[26] Norimasa Yoshida and Takafumi Saito. 2012. The Evolutes of Log-Aesthetic Planar Curves and the Drawable Boundaries of the Curve Segments. ComputerAided Design and Applications 9, 5 (2012), 721–731. https://doi.org/10.3722/ cadaps.2012.721-731
[27] Fabian Yzerman. 2020. Fast approaches to simplify and offset Bézier curves within specified error limits. https://blend2d.com/research/simplifyandoffset_ bezier_curves.pdf
:::info
Authors:
- Raph Levien
- Arman Uguray
:::
:::info
This paper is available on arxiv under CC 4.0 license.
:::