A Graph Transformer Network for Predicting Remaining Process Time | HackerNoon

Table of Links

Abstract and 1. Introduction

2. Background and Related work

3. Preliminaries

4. PGTNet for Remaining Time Prediction

   4.1 Graph Representation of Event Prefixes

   4.2 Training PGTNet to Predict Remaining Time

5. Evaluation

   5.1 Experimental Setup

   5.2 Results

6. Conclusion and Future Work, and References

5 Evaluation

This section presents the experiments used to evaluate the performance of PGTNet for remaining time prediction. Table 1 summarizes the characteristics of the 20 publicly available event logs used as a basis for this. In the remainder, Section 5.1 describes the experimental setup, followed by the results in Section 5.2. Our employed implementation and additional results are available in our project’s public repository.[3]

5.1 Experimental Setup

Data preprocessing. We filter out traces with fewer than 3 events, since our approach requires an event prefix of at least length 2 to make a prediction. Aside from that, we do not apply any preprocessing to the available event logs.

Benchmark approaches. We compare our approach against four others:

– DUMMY : A simple baseline that predicts the average remaining time of all training prefixes with the same length k as a given prefix.

– DALSTM [13]: An LSTM-based approach that was recently shown to have superior results among LSTMs used for remaining time prediction [15].

– ProcessTransformer [2]: A transformer-based approach designed to overcome LSTM’s limitations in capturing long-range dependencies.

– GGNN [3]: An approach that utilizes gated graph neural networks to incorporate control-flow relationships into the learning process. It employs gated recurrent unit (GRU) within its MPNN layers, enabling the learning of the sequential nature of graph nodes.

Data split. There is no consensus on the data split for predictive process monitoring. Some papers employed a chronological holdout split [2,17], while others opted for cross-validation [5, 14, 15]. The holdout split maintains chronological order but may introduce instability due to end-of-dataset bias. To avoid such instability, additional data preprocessing, as suggested by [23], is necessary.

As our benchmark approaches were not trained with such preprocessing, we avoided additional steps and chose a 5-fold cross-validation data split (CV=5) to enhance model’s robustness against the end-of-dataset bias. We randomly partition the dataset into 5 folds where each fold serves as a test set once, and the remaining four folds are used as training and validation sets. For completeness, we also report results obtained using holdout data splits in our supplementary GitHub repository.

Prefix establishment. We turn the three sets of traces (training, validation, and test) into three sets of event prefixes by taking the event prefixes for each length 1 < k < |σ| per trace. In contrast to [2, 13], we excluded event prefixes of length 1 because a minimum of two events is required to form the graph representation of an event prefix. Moreover, similar to [13], we excluded complete prefixes (i.e., k = |σ|) because predicting the remaining time for such prefixes often lacks practical value.

– PE/SE modules: LapPE+RWSE [4, 10] serves as the default module, occasionally substituted by Graphormer [24]. By default, DeepSet [25] processes PE/SEs, with SignNet [11] replacing LapPE+RWSE and DeepSet in some experiments. PE/SEs are tested in two sizes: 8 and 16.

– Embedding modules: Nodes and edges use an embedding size of 64. Edge features are compressed using two fully-connected layers, though in some experiments we opt for a single layer.

– Processing modules: comprising 5 GPS layers (GIN + Transformer) [16] with 8 heads, utilizing a dropout of 0.0 for MPNN blocks and 0.5 for Transformer blocks. In some experiments, we used 10 GPS layers with 4 heads instead, while in others we applied a dropout of 0.2 for MPNN blocks.

– Readout layer: Mean pooling is the default configuration, occasionally replaced by sum pooling.

Our focus is on demonstrating PGTNet’s applicability for remaining time prediction rather than an exhaustive hyperparameter search. Therefore, we evaluated a limited set of configurations per log, selecting the best based on validation loss.

Evaluation metrics. We used Mean Absolute Error (MAE) to measure prediction accuracy. Since we are interested in models that not only have smaller MAE but also can make accurate predictions earlier, allowing more time for corrective actions, we used the method proposed in [17], which evaluates MAE across different event prefix lengths. This approach provides insights into the predictive performance of the model as more events arrive.

5.2 Results

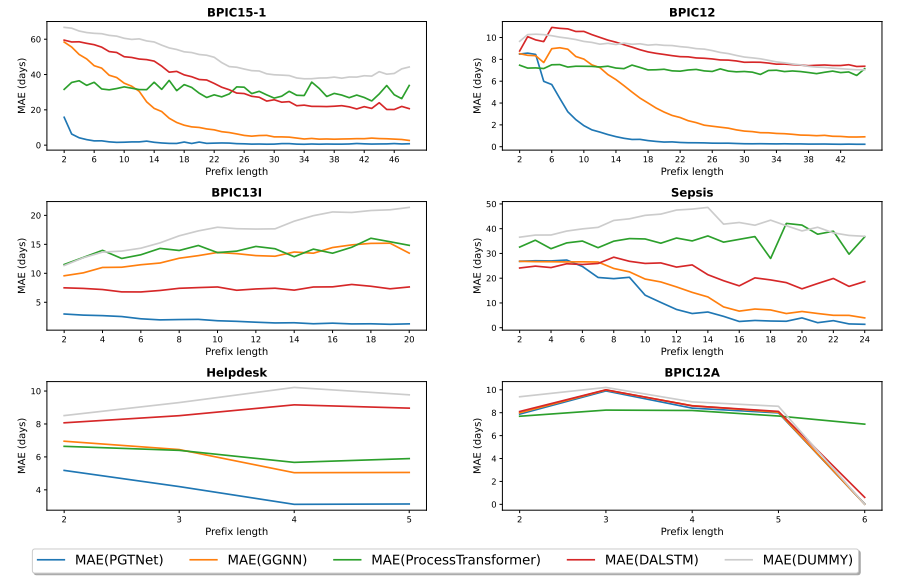
Overall results. Table 2 summarizes the experimental results for the 20 event logs, providing the average and standard deviations of the MAEs obtained over experiments with three distinct, random seeds for training and evaluation. The table shows that our approach consistently outperforms the benchmark approaches across the 20 event logs, yielding an average MAE of 12.92, compared to 24.63 for the next best approach (GGNN).

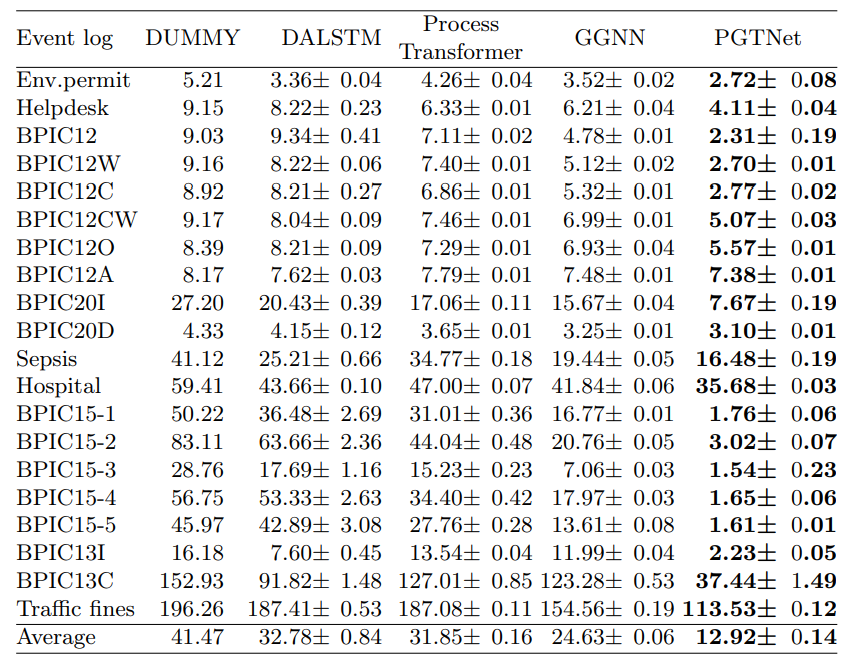
Next to these absolute MAE scores, we also computed the relative MAE (i.e., the MAE divided by the average case duration per log) to account for differences in the cycle times across event logs. Using these relative scores, we can visualize the accuracy improvements across different logs, as done in Figure 3 (for clarity, we aggregated the results of logs that stem from the same BPI collection, e.g., averaging the results of all BPIC15 logs).

PGTNet also excels in earliness of predictions, achieving lower MAE for most prefix lengths across all event logs. We illustrate some of these results in Figure 4, which depicts MAE trends for BPIC15-1, BPIC12, BPIC13I, Sepsis, Helpdesk, and BPIC12A logs at various prefix lengths. These six logs are representative of major MAE trends that we observed across the 20 event logs (the remaining

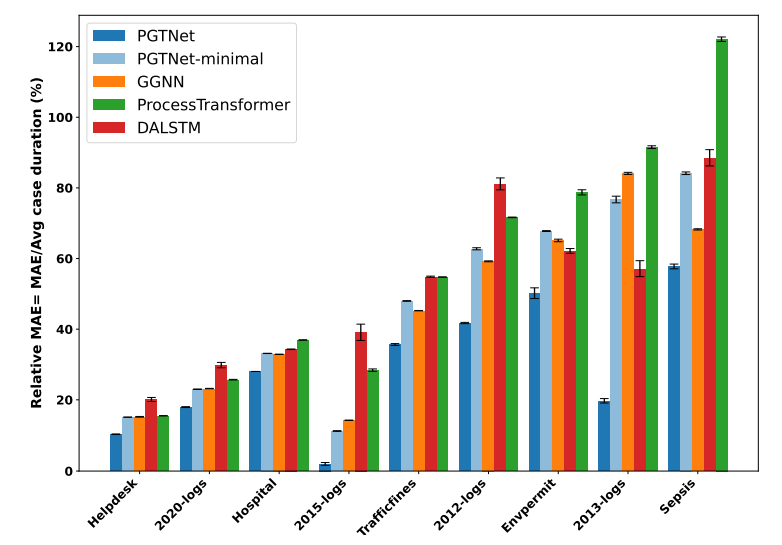
figures are available in our repository). To improve understandability, we exclude uncommonly long prefixes from the visualization, so that Figure 4 focuses on prefixes up to a length that corresponds to 90% of all prefixes in each dataset.

Summarizing the overall results in terms of MAE, relative MAE, and prediction earliness, we obtain the following main insights:

– In 11 out of 20 logs, PGTNet achieves an MAE improvement of over 50% compared to the best baseline approach. For five BPIC15 and two BPIC13 logs, MAE trends closely mirror those of BPIC15-1 and BPIC13I as depicted in Figure 4. In BPIC12, BPIC12W, BPIC12C, and BPIC20I, the MAE trends closely follow those observed in BPIC12. In BPIC15 and BPIC12 logs, ProcessTransformer is the best baseline approach for short prefixes, whereas GGNN exhibits competitive performance only after execution of a substantial number of events. Notably, in the BPICS13 event logs, DALSTM outperforms other baseline approaches.

– In another 7 logs, PGTNet exhibits considerable improvement in MAE (15% to 35%), with Traffic fines, Env.permit and BPIC12O showing similar MAE trends to Helpdesk log in Figure 4. MAE trends for BPIC12CW resemble those of other BPIC12 logs in the first group. Notably, the Sepsis log shows a distinct MAE trend, where GGNN achieves comparable results to PGTNet for most prefix lengths.

– For BPIC20D and BPIC12A, the improvement is more modest, with the latter case yielding nearly identical MAEs for all prefix lengths (see Figure 4).

Ablation study. The remarkable performance of PGTNet can be attributed to a synergy between the expressive capacity of the employed architecture and the incorporation of diverse process perspectives into the graph representation of event prefixes. To distinguish the impacts of these factors, we conducted an ablation study for which we trained a minimal PGTNet model, relying solely on edge weights (i.e., control-flow) and temporal features, thus omitting data attributes from consideration. We used identical hyperparameters and configurations as was done for the complete PGTNet model. Hence, the ablation study establishes a lower boundary for contribution of the PGTNet’s architecture.

Our experiments reveal that the minimal PGTNet model consistently outperforms ProcessTransformer in terms of MAE (see Figure 3). This underscores PGTNet’s capabilities in capturing both local and global contexts, which is advantageous for predicting remaining time. However, the predictive performance of the minimal PGTNet is comparable to that of the GGNN approach, suggesting that learning from local control-flow structures in MPNN blocks (done by GGNN) holds greater significance than capturing long-range dependencies (as done by ProcessTransformer). This observation is further supported by the overall results presented in Table 2, where GGNN outperforms DALSTM and ProcessTransformer in all event logs, except for two BPIC13 logs. Additionally, the contribution of the architecture and the incorporation of extra data attributes varies across different event logs. While the PGTNet’s architecture plays a decisive role for logs such as BPIC15 and BPIC20I, the improvements in MAE for logs such as BPICS12 and BPICS13 is primarily due to the incorporation of additional features. Further details regarding our ablation study can be found in our repository.

Impact of process complexity. The MAE improvement achieved by PGTNet varies significantly across different event logs. Investigating these variations, we correlated process complexity metrics from [1, 21] with MAE improvements achieved by PGTNet. Notably, our approach outperforms alternatives when the number of process variants increases rapidly with respect to the number of cases. This trend extends to other variation metrics, including ‘structure’ (average distinct activities per case) and ‘level of detail’ (number of acyclic paths in the transition matrix) [1]. In terms of size metrics, PGTNet exhibits superior performance with increasing average trace length and/or number of distinct activities. The most significant positive correlation is observed for ‘normalized sequence entropy’, a graph entropy metric adept at capturing both variation and size complexity [1].

This reveals that PGTNet excels in highly flexible and complex processes, where benchmark approaches may overlook sparse but meaningful directly-follows relations among activities. The graph representation, detailed in Section 4.1, converts different process variants into non-isomorphic graphs with varying nodes, connectivity structures, and edge weights. Graph isomorphism network (GIN) modules, renowned for distinguishing non-isomorphic graphs [8], process this graph-oriented data. Simultaneously, Transformer blocks capture long-range dependencies. In complex processes like BPIC15, GIN blocks benefit from diverse set of non-isomorphic graphs available for learning, while Transformer blocks leverage insightful PE/SEs, thus providing a synergy that results in a remarkable reduction in MAE

Training, and inference time. We conducted experiments using an Nvidia RTX A6000 GPU, with training and inference times detailed in Table 3. For training time, we computed the sum of training time for all cross-validation data splits and then averaged these times across all 20 event logs. Regarding average inference time, we compute the time to infer the remaining time per event prefix and report the average inference time across all event logs.

In terms of training time, DALSTM and ProcessTransformer, which use shallow neural networks (either with 2 LSTM layers or 1 self-attention layer), can be trained an order of magnitude faster than the graph-based approaches, though PGTNet is still trained faster than GGNN (12.93 vs. 18.56 hours). We see a similar trend in terms of inference times, though essentially all approaches are reasonably fast here, with PGTNet being the slowest with an average time just below 3 miliseconds.

6 Conclusion and Future Work

This paper introduces a novel approach employing Process Graph Transformer Networks (PGTNet) to predict the remaining time of running business process instances. Our approach consists of a data transformation from an event log to a graph dataset, and training a neural network based on the GPS Graph Transformer recipe [16]. Our graph representation of event prefixes incorporates multiple process perspectives and also enables integration of control-flow relationships among activities into the learning process. This graph-oriented data input is subsequently processed by PGTNet, which strikes a balance between learning from local contexts and long-range dependencies.

Through experiments conducted on 20 real-world datasets, our results demonstrate the superior accuracy and earliness of predictions achieved by PGTNet compared to the existing deep learning approaches. Notably, our approach exhibits exceptional performance for highly flexible and complex processes, where the performance of LSTM, Transformer and GGNN architectures falls short.

While originally designed for predicting remaining times, our approach has the potential to learn high-level event prefix representations, rendering it applicable to other tasks, including next activity prediction and process outcome prediction. In future research, we therefore aim to apply PGTNet for these tasks, whereas we also aim to improve the predictive accuracy of our approach by investigating the potential of multi-task learning and exploring different positional and structural embeddings, as well as varying graph representations. Finally, we aim to extend our approach to also be applicable to object-centric event logs.

Reproducibility: Our source code and all evaluation results are accessible in our repository: https://github.com/keyvan-amiri/PGTNet

References

1. Augusto, A., Mendling, J., Vidgof, M., Wurm, B.: The connection between process complexity of event sequences and models discovered by process mining. Information Sciences 598, 196–215 (2022)

2. Bukhsh, Z.A., Saeed, A., Dijkman, R.M.: ProcessTransformer: Predictive Business Process Monitoring with Transformer Network (2021), arXiv:2104.00721 [cs]

3. Duong, L.T., Travé-Massuyès, L., Subias, A., Merle, C.: Remaining cycle time prediction with Graph Neural Networks for Predictive Process Monitoring. In: International Conference on Machine Learning Technologies (ICMLT). ACM (2023)

4. Dwivedi, V.P., Luu, A.T., Laurent, T., Bengio, Y., Bresson, X.: Graph Neural Networks with Learnable Structural and Positional Representations (2022), arXiv:2110.07875 [cs]

5. Evermann, J., Rehse, J.R., Fettke, P.: Predicting process behaviour using deep learning. Decision Support Systems 100, 129–140 (2017)

6. Gilmer, J., Schoenholz, S.S., Riley, P.F., Vinyals, O., Dahl, G.E.: Neural message passing for quantum chemistry. In: Precup, D., Teh, Y.W. (eds.) Proceedings of the 34th International Conference on Machine Learning. Proceedings of Machine Learning Research, vol. 70, pp. 1263–1272. PMLR (2017)

7. Harl, M., Weinzierl, S., Stierle, M., Matzner, M.: Explainable predictive business process monitoring using gated graph neural networks. Taylor and Francis (2020)

8. He, T., Zhang, Z., Zhang, H., Zhang, Z., Xie, J., Li, M.: Bag of tricks for image classification with convolutional neural networks. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2019)

9. Hu, W., Liu, B., Gomes, J., Zitnik, M., Liang, P., Pande, V., Leskovec, J.: Strategies for Pre-training Graph Neural Networks (2020), arXiv:1905.12265 [cs, stat]

10. Kreuzer, D., Beaini, D., Hamilton, W.L., Létourneau, V., Tossou, P.: Rethinking Graph Transformers with Spectral Attention (2021), arXiv:2106.03893 [cs]

11. Lim, D., Robinson, J., Zhao, L., Smidt, T., Sra, S., Maron, H., Jegelka, S.: Sign and Basis Invariant Networks for Spectral Graph Representation Learning (2022), arXiv:2202.13013 [cs, stat]

12. Loshchilov, I., Hutter, F.: Decoupled Weight Decay Regularization (2019), arXiv:1711.05101 [cs, math]

13. Navarin, N., Vincenzi, B., Polato, M., Sperduti, A.: LSTM networks for data-aware remaining time prediction of business process instances. In: 2017 IEEE Symposium series on Computational Intelligence (SSCI). pp. 1–7 (2017)

14. Polato, M., Sperduti, A., Burattin, A., de Leoni, M.: Data-aware remaining time prediction of business process instances. In: 2014 International Joint Conference on Neural Networks (IJCNN). pp. 816–823 (2014)

15. Rama-Maneiro, E., Vidal, J.C., Lama, M.: Deep Learning for Predictive Business Process Monitoring: Review and Benchmark. IEEE Transactions on Services Computing 16(1), 739–756 (2023)

16. Rampášek, L., Galkin, M., Dwivedi, V.P., Luu, A.T., Wolf, G., Beaini, D.: Recipe for a General, Powerful, Scalable Graph Transformer. NeurIPS 35, 14501–14515 (2022)

17. Tax, N., Verenich, I., La Rosa, M., Dumas, M.: Predictive Business Process Monitoring with LSTM Neural Networks. In: Advanced Information Systems Engineering. pp. 477–492. Springer International Publishing, Cham (2017)

18. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, Ł., Polosukhin, I.: Attention is All you Need. In: NeurIPS. vol. 30. Curran Associates, Inc. (2017)

19. Venugopal, I., Töllich, J., Fairbank, M., Scherp, A.: A Comparison of DeepLearning Methods for Analysing and Predicting Business Processes. In: 2021 International Joint Conference on Neural Networks (IJCNN). pp. 1–8 (2021)

20. Verenich, I., Dumas, M., Rosa, M.L., Maggi, F.M., Teinemaa, I.: Survey and Crossbenchmark Comparison of Remaining Time Prediction Methods in Business Process Monitoring. ACM Trans. on Intelligent Systems and Technology 10(4), 34:1– 34:34 (2019)

21. Vidgof, M., Wurm, B., Mendling, J.: The Impact of Process Complexity on Process Performance: A Study using Event Log Data (2023), arXiv:2307.06106 [cs]

22. Weinzierl, S.: Exploring Gated Graph Sequence Neural Networks for Predicting Next Process Activities. In: BPM Workshops. pp. 30–42. Springer (2022)

23. Weytjens, H., De Weerdt, J.: Creating Unbiased Public Benchmark Datasets with Data Leakage Prevention for Predictive Process Monitoring. In: BPM Workshops. pp. 18–29. Springer International Publishing, Cham (2022)

24. Ying, C., Cai, T., Luo, S., Zheng, S., Ke, G., He, D., Shen, Y., Liu, T.Y.: Do Transformers Really Perform Badly for Graph Representation? In: NeurIPS. vol. 34, pp. 28877–28888. Curran Associates, Inc. (2021)

25. Zaheer, M., Kottur, S., Ravanbakhsh, S., Poczos, B., Salakhutdinov, R.R., Smola, A.J.: Deep Sets. In: NeurIPS. vol. 30. Curran Associates, Inc. (2017)

:::info
Authors:

(1) Keyvan Amiri Elyasi[0009 −0007 −3016 −2392], Data and Web Science Group, University of Mannheim, Germany ([email protected]);

(2) Han van der Aa[0000 −0002 −4200 −4937], Faculty of Computer Science, University of Vienna, Austria ([email protected]);

(3) Heiner Stuckenschmidt[0000 −0002 −0209 −3859], Data and Web Science Group, University of Mannheim, Germany ([email protected]).

:::

:::info
This paper is available on arxiv under CC BY-NC-ND 4.0 Deed (Attribution-Noncommercial-Noderivs 4.0 International) license.

:::

[3] https://github.com/keyvan-amiri/PGTNet