:::info
Author:
(1) Pedro Duarte Gomes, Department of Mathematics, University of Copenhagen.
:::
Table of Links
Abstract
-
Keywords and 2. Introduction
-
Set up
-
From Classical Results into Differential Machine Learning
4.1 Risk Neutral Valuation Approach
4.2 Differential Machine learning: building the loss function
-
Example: Digital Options
-
Choice of Basis
6.1 Limitations of the Fixed-basis
6.2 Parametric Basis: Neural Networks
-
Simulation-European Call Option
7.1 Black-Scholes
7.2 Hedging Experiment
7.3 Least Squares Monte Carlo Algorithm
7.4 Differential Machine Learning Algorithm
-
Numerical Results
-
Conclusion
-
Conflict of Interests Statement and References
Notes
Abstract
This article introduces the groundbreaking concept of the financial differential machine learning algorithm through a rigorous mathematical framework. Diverging from existing literature on financial machine learning, the work highlights the profound implications of theoretical assumptions within financial models on the construction of machine learning algorithms.
This endeavour is particularly timely as the finance landscape witnesses a surge in interest towards data-driven models for the valuation and hedging of derivative products. Notably, the predictive capabilities of neural networks have garnered substantial attention in both academic research and practical financial applications.
The approach offers a unified theoretical foundation that facilitates comprehensive comparisons, both at a theoretical level and in experimental outcomes. Importantly, this theoretical grounding lends substantial weight to the experimental results, affirming the differential machine learning method’s optimality within the prevailing context.
By anchoring the insights in rigorous mathematics, the article bridges the gap between abstract financial concepts and practical algorithmic implementations.
1 Keywords
Differential Machine Learning, Risk Neutral valuation, Derivative Pricing, Hilbert Spaces Orthogonal Projection, Generalized Function Theory
2 Introduction
Within the dynamic landscape of financial modelling, the quest for reliable pricing and hedging mechanisms persists as a pivotal challenge. This article aims to introduce an encompassing theory of pricing valuation uniquely rooted in the domain of machine learning. A primary focus lies in overcoming a prominent hurdle encountered in implementing the differential machine learning algorithm, specifically addressing the critical need for unbiased estimation of differential labels from data sources, as highlighted in studies by Huge (2020) and Broadie (1996). This breakthrough holds considerable importance for contemporary practitioners across diverse institutional settings, offering tangible solutions and charting a course toward refined methodologies. Furthermore, this endeavour not only caters to the immediate requirements of practitioners but also furnishes invaluable insights that can shape forthcoming research endeavours in this domain.
The article sets off from the premise that the pricing and hedging functions can be thought of as elements of a Hilbert space, in a similar way as Pelsser and Schweizer, 2016. A natural extension of these elements across time, originally attained in the current article, is accomplished by the Hahn Banach extension theorem, an extension that would translate as an improvement of the functional through the means of the incorporation of the accumulating information. This functional analytical approach conveys the necessary level of abstraction to justify, and discuss the different possibilities of implementation of the financial models contemplated in Huge and Savine, 2020 and Pelsser and Schweizer, 2016. So, a bridge will be built from the deepest theoretical considerations into the practicality of the implementations, keeping as a goal mathematical rigour in the exposition of the arguments. Modelling in Hilbert spaces allows the problem to be reduced into two main challenges: the choice of a loss function and the choice of an appropriate basis function. A discussion about the virtues and limitations of two main classes of basis functions is going to unravel, mainly supported by the results in Hornik et al., 1989,Barron, 1993 and Telgarsky, 2020. A rigorous mathematical derivation of the loss functions, for the two different risk-neutral methods, is going to be exposed, where the result for the second method, was stated and proven originally in the current document. The two methods are the Least Squares Monte Carlo and the Differential machine learning, inspired in Pelsser and Schweizer, 2016 and Huge and Savine, 2020, respectively. It is noted that the first exposition of the Least Squares Monte Carlo Method was accomplished in Longstaff and Schwartz, 2001. The derivation of the differential machine learning loss function using generalized function theory allows us to relax the assumptions of almost sure differentiability and almost sure Lipschitz continuity of the pay-off function in Broadie and Glasserman, 1996. Instead, the unbiased estimate of the derivative labels only requires the assumption of local integrability of the pay-off function, which it must clearly satisfy, given the financial context. This allows the creation of a technique to obtain estimates of the labels for any derivative product, solving the biggest limitation in Huge and Savine, 2020. The differential machine learning algorithm efficiently computes differentials as unbiased estimates of ground truth risks, irrespective of the transaction or trading book, and regardless of the stochastic simulation model.
The implementations are going to be completely justified by the arguments developed in the theoretical sections. The implementation of the differential machine learning method relies on Huge and Savine, 2020. The objective of this simulation is to assess the effectiveness of various models in learning the Black-Scholes model within the context of a European option contract. Initially, a comparison will be drawn between the prices and delta weights across various spot prices. Subsequently, the distribution of Profit and Loss (PnL) across different paths will be examined, providing the relative hedging errors metric. These will serve the purpose of illustrating theoretical developments.
3 Set up
Since the dual of a Hilbert space is itself a Hilbert space,g can be considered a functional.[3]
Considering the sequence of conditional Hilbert spaces:

Now the pricing or hedging functional incorporates the accumulated information from period 0 to period l.
This allows us to see that the increasing information would shape the function, which is something well-seen, in statistical learning, with the use of increasing training sets defined across time. [4]
We will begin by dwelling upon the problem of how to find function g, developing the theoretical statistical objects that are necessary for that aim. The aim is to estimate the pricing or hedging functions. So, a criterion needs to be established in the theoretical framework.
Let Z and X be two respectively d and p dimensional real-valued random variables, following some unknown joint distribution p(z, x). The expectation of the loss function associated with a predictor g can be defined as:
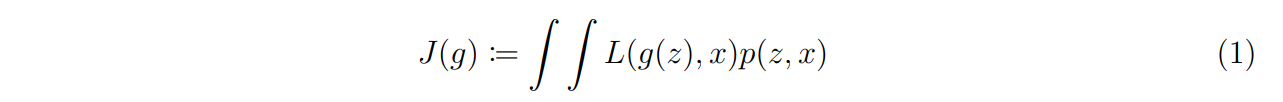
The objective is to find the element g ∈ H which achieves the smallest possible expected loss. Assume a certain parameter vector θ ∈ Θ, where Θ is a compact set in the Euclidean space. As the analytical evaluation of the expected value is impossible, a training sample (zi , xi) for i = 1, …, n drawn from p(z, x) is collected. An approximate solution to the problem can then be found by minimising the empirical approximation of the expected loss:
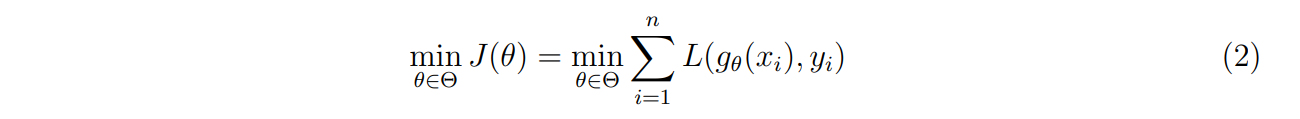
:::info
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
:::
[1] H represents all prior knowledge, one of the common constraints for option pricing are non-negativity and positiveness on the second order derivatives
[2] Even when Z is expressed as a diffusion, T is finite so the different paths could never display infinite variance
[3] This property is easily verified by building the following map ϕH′ → H, defined by ϕ(v) = fv, where fv(x) = ⟨x, v⟩, for x ∈ H is an antilinear bijective isometry.
[4] The functional analytical results can be revisited by the reader in Rudin, 1974












