Table of Links
Abstract and 1. Introduction
-
Related Works
-
Convex Relaxation Techniques for Hyperbolic SVMs
3.1 Preliminaries
3.2 Original Formulation of the HSVM
3.3 Semidefinite Formulation
3.4 Moment-Sum-of-Squares Relaxation
-
Experiments
4.1 Synthetic Dataset
4.2 Real Dataset
-
Discussions, Acknowledgements, and References
A. Proofs
B. Solution Extraction in Relaxed Formulation
C. On Moment Sum-of-Squares Relaxation Hierarchy
D. Platt Scaling [31]
E. Detailed Experimental Results
F. Robust Hyperbolic Support Vector Machine
3 Convex Relaxation Techniques for Hyperbolic SVMs
In this section, we first introduce fundamentals on hyperbolic spaces and the original formulation of the hyperbolic Support Vector Machine (HSVM) due to Cho et al. [4]. Next, we present two relaxations techniques, the semidefinite relaxation and the moment-sum-of-squares relaxation, that can be solved efficiently with convergence guarantees. Our discussions center on the Lorentz manifold as the choice of hyperbolic space, since it has been shown in Mishne et al. [6] that the Lorentz formulation offers greater numerical advantages in optimization.
3.1 Preliminaries
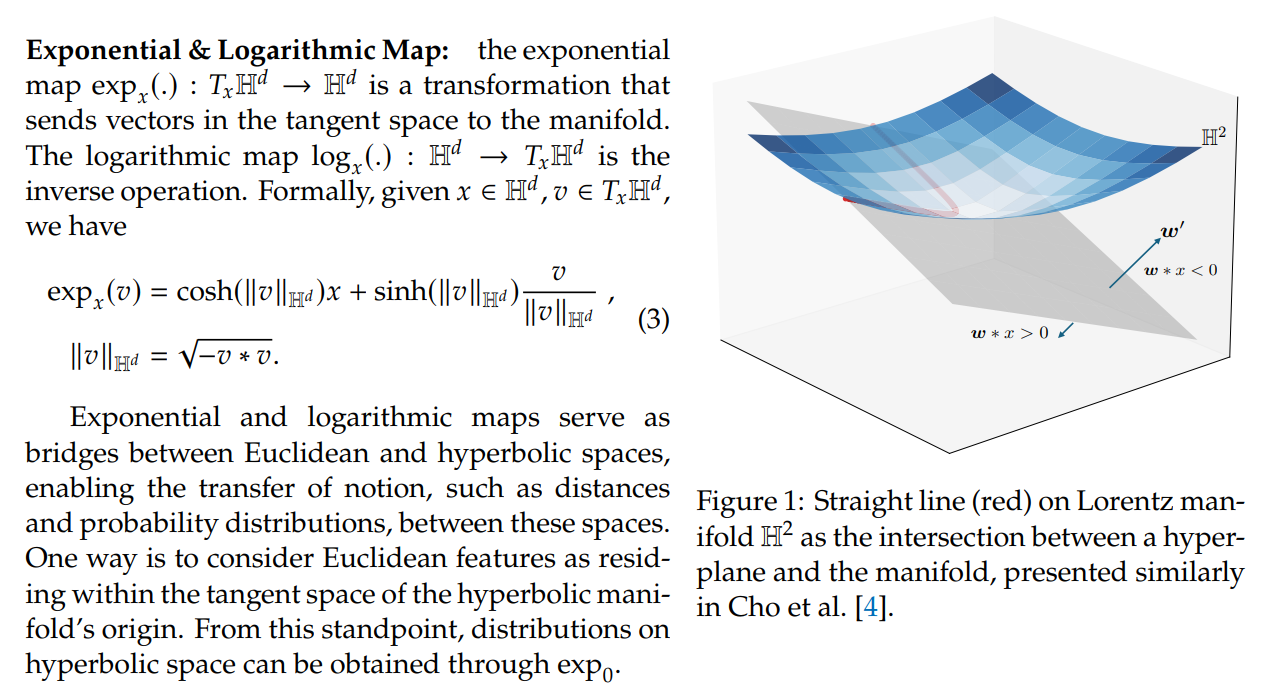

:::info
Authors:
(1) Sheng Yang, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA ([email protected]);
(2) Peihan Liu, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA ([email protected]);
(3) Cengiz Pehlevan, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, Center for Brain Science, Harvard University, Cambridge, MA, and Kempner Institute for the Study of Natural and Artificial Intelligence, Harvard University, Cambridge, MA ([email protected]).
:::
:::info
This paper is available on arxiv under CC by-SA 4.0 Deed (Attribution-Sharealike 4.0 International) license.
:::











