Can a Financial Model Truly Mimic Reality? These Numbers Say Yes | HackerNoon

Table of Links

Abstract, Acknowledgements, and Statements and Declarations

1. Introduction

2. Background and Related Work

   2.1 Agent-based Financial Market simulation

   2.2 Flash Crash Episodes

3. Model Structure and 3.1 Model Set-up

   3.2 Common Trader Behaviours

   3.3 Fundamental Trader (FT)

   3.4 Momentum Trader (MT)

   3.5 Noise Trader (NT)

   3.6 Market Maker (MM)

   3.7 Simulation Dynamics

4. Model Calibration and Validation and 4.1 Calibration Target: Data and Stylised Facts for Realistic Simulation

   4.2 Calibration Workflow and Results

   4.3 Model Validation

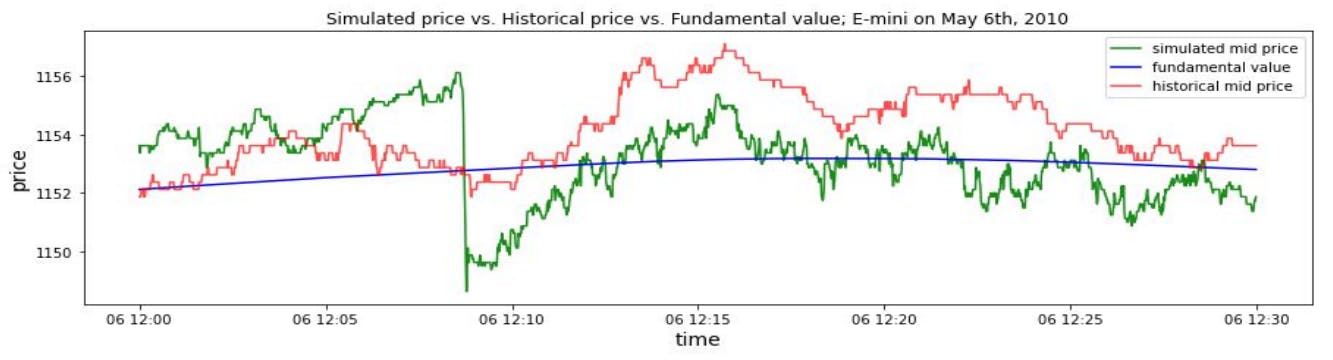
5. 2010 Flash Crash Scenarios and 5.1 Simulating Historical Flash Crash

   5.2 Flash Crash Under Different Conditions

6. Mini Flash Crash Scenarios and 6.1 Introduction of Spiking Trader (ST)

   6.2 Mini Flash Crash Analysis

   6.3 Conditions for Mini Flash Crash Scenarios

7. Conclusion and Future Work

   7.1 Summary of Achievements

   7.2 Future Works

References and Appendices

4.3 Model Validation

Table 2 shows the stylised facts distance of the calibrated model. However, the value itself does not present an intuitive description of how well the simulated data fit empirical data. A cross-check on the validity of our model topology and calibration strategy is needed. Following Franke and Westerhoff (2012), two metrics are used for assessing the quality of the moment matching and the validity of the model simulation: the moment-specific p-value and the moment coverage ratio.

4.3.1 Statistical Hypothesis Testing: Moment-specific p-value

The stylised facts distance provides us with numerical values for the realism of the simulation. However, one more elementary question needs to be addressed: whether the data generated by model calibration and simulation would be rejected by the empirical data. The question is answered by calculating a moment-specific p-value as a statistical hypothesis test.

Recall that in Section 4.1.4 the weights are calculated by the block bootstrapping method proposed in Franke and Westerhoff (2012). While the variance of block bootstrapping samples is the corresponding weight for each part of the loss function, the large number of samples obtained in this procedure can also be used to apply the loss function D to them. In this way an entire frequency distribution of values of D is available, which can subsequently be contrasted with the simulated distribution of values of D. The fundamental idea is that the set of bootstrapped samples of return time series is a proxy of the set of different return time series samples that could be produced if the hypothetical real-world data generation process exists. Accordingly, if a simulated return time series yields a value of D within the range of the bootstrapped values of D, this simulated return time series is difficult to be distinguished from a real-world series.

From Table 3 we can see that for all trading day in the collected dataset, the moment-specific p-values are greater than 0.05. Consequently, we cannot reject the null hypothesis which specifies that the simulated return time series belong to the same distribution as the empirical return time series. This statistical hypothesis testing gives evidence that the calibrated model is capable of generating realistic financial price time series.

4.3.2 Moment Coverage Ratio

The previous evaluation of the model was based on the values of the stylised facts distance function D. While statistical testing enables us to evaluate the validity of the model simulation, the quality of moment matching for each specific moment is still unknown. Another potential issue is that the stylised facts distance function D is the optimisation target during the calibration process. Thus the evaluation metric involving the distance D may be biased because of the potential overfitting problem. To address the above problems, the “moment coverage ratio” (MCR) metric is adopted to assess the degree of moment matching, taking into account each specific moment. The moment coverage ratio is originally proposed in Franke and Westerhoff (2012). The basis for moment coverage ratio calculation is the concept of a confidence interval of the empirical moments. Consistent with Franke and Westerhoff (2012), the 95% confidence interval of a moment is considered, which is defined to be the interval with boundaries ±1.96 times the standard deviation around the empirical value of this moment. The next step is to determine the standard deviation for each empirical moment. Franke and Westerhoff (2012) apply the delta method to the autocorrelation coefficients to calculate the standard deviation. In this paper, we use a more direct way to obtain the empirical standard deviation, which is based on the block bootstrapping method. Recall that large quantities of return time series are obtained by the block bootstrapping method. For each specific moment, a moment value can be calculated out of every sampled return series. In total there will be B values for each moment, where B is the bootstrapping sample number. The standard deviation of those values is considered to be the standard deviation for the corresponding empirical moment. One may feel uneasy about the bootstrapping of the autocorrelation functions at the longer lags since the method alters the temporal order of the return series. However, the block size in our block bootstrapping method is 1800, which is significantly larger than the longest lag (90) in the autocorrelation functions. Consequently, the impact of bootstrapped block re-ordering on the autocorrelation functions is negligible.

With the standard deviation on hand, the corresponding confidence interval for each specific moment is immediately available. In this way an intuitive criterion for assessing a simulated return series is obtained: if all of its moments are contained in the confidence intervals, the simulated return series cannot be rejected as being incompatible with empirical data. Nonetheless, one single simulation is not sufficient to evaluate a model as a whole due to the sample variability. In addition, it is likely that for one simulated return series some moments are contained in the confidence interval while others are not. It goes without saying that considering multiple simulation runs of the model will provide a more exhaustive assessment of the model performance. Specifically, for each simulation run the confidence interval check is repeated. We count the number of Monte Carlo simulation runs in which the single moments are contained in the corresponding confidence intervals. The corresponding percentage numbers out of all Monte Carlo runs are defined as the moment coverage ratio.

Since the model is calibrated by each trading day, Monte Carlo simulation is run for each trading day and the corresponding moment coverage ratios are calculated to evaluate the calibrated model. Table 4 presents the results of the moment coverage ratios calculation. Except for the volatility moment on May 3rd and the 90-lag squared return autocorrelation moment on May 4th, all other moment coverage ratios are higher than 50%. According to the analysis in Franke and Westerhoff (2012), the higher than 50% moment coverage ratio represents a terrific performance of the model. In addition, almost half of the moment coverage ratios are even higher than 90%, which indicates that our calibrated model has an excellent ability to reproduce realistic stylised facts. Overall, with respect to the selected moments, the calibrated model’s capability of matching empirical moments and reproducing realistic stylised facts is highly remarkable.