Table of Links
Abstract
-
Keywords and 2. Introduction
-
Set up
-
From Classical Results into Differential Machine Learning
4.1 Risk Neutral Valuation Approach
4.2 Differential Machine learning: building the loss function
-
Example: Digital Options
-
Choice of Basis
6.1 Limitations of the Fixed-basis
6.2 Parametric Basis: Neural Networks
-
Simulation-European Call Option
7.1 Black-Scholes
7.2 Hedging Experiment
7.3 Least Squares Monte Carlo Algorithm
7.4 Differential Machine Learning Algorithm
-
Numerical Results
-
Conclusion
-
Conflict of Interests Statement and References
Notes
4 From Classical Results into Differential Machine Learning
4.1 Risk Neutral Valuation Approach
The following section discusses two methods: the Least Squares Monte Carlo and the Differential Machine Learning method. The aim is to construct a loss function under the assumption of risk neutrality. We will derive the corresponding loss function and establish two analogous propositions, illustrating the power of the theoretical construction presented earlier. This unique perspective allows for a comprehensive comparison of the two methods, which has not been explored in the existing literature.
As in Cox, 2000, the valuation of a derivative contract involves the functional g0,t representing the expected conditional value:
The objective is to compute the expectation of X conditional on information at time t. Note that Q is not necessarily unique, meaning there might not be market completeness.
4.2 Differential Machine learning: building the loss function
The main interest lies in estimating equation (3) to obtain the price of the derivative. This result contributes to the construction of the Differential Machine Learning approach. The following result is widely known in the literature and can be revisited by the reader in Pelsser and Schweizer, 2016.
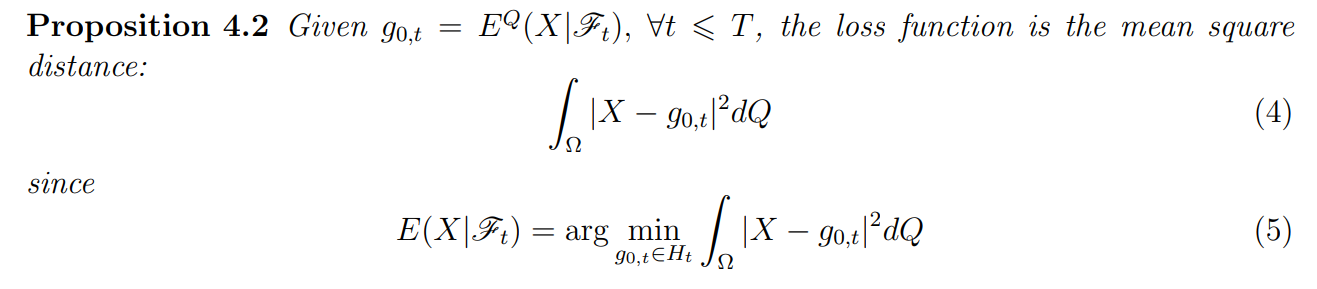
The proposition that characterizes the Differential Machine learning method is originally stated and proven in the current document. Its proof is essential to understand the implementation of this method, such as how to compute unbiased estimates of the labels for the differentials.

The ∆ would be computed as:
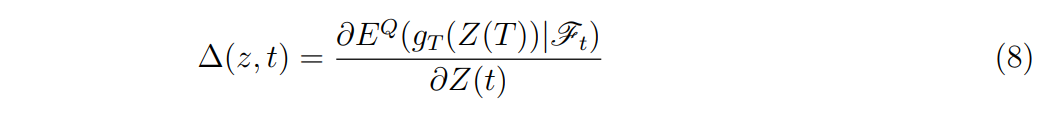
which measures the derivative price sensitivity in relation to oscillations of the underlying.
If the differentiation could go inside the conditional expectation, an estimator for ∆ can be created through discretization methods. That would imply that H would need to be restricted to the differentiable elements. An analogous proof to the one of the proposition would be achieved if the space with differentiable elements that have is a separable Hilbert space.
However, pay-off functions are non-differentiable or even discontinuous as in the case of the European standard options and digital options respectively. So a broader concept of derivative needs to be defined. Generalized function theory allows a less abstract approach to weak derivative definition compared to distribution theory as in Rudin, 1974.
To assure the unbiasedness of the ∆ estimator, there is a need for a result that supports the passage of the derivative inside the expectation. The following result is not a very well-known result and can be found in the seventh chapter of Jones, 1966

Assuming that the pay-off function is locally integrable, as it is something expected in financial theory, once the conditional mean of the pay-offs across time is the price of the derivative product, given its idiosyncratic characteristics. This solves the main problem in Broadie and Glasserman, 1996, by only requiring the pay-off function to be locally integrable.
Applying proposition 3.4 to equation 8:
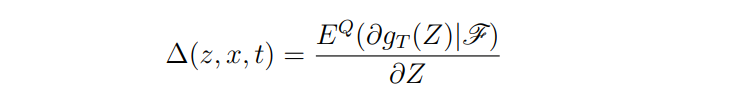
The aim now is to construct a space that accounts for the ∂g(Z, T), so that it defines a separable Hilbert space.
This will lead to the theory on the Sobolev spaces, once the latter account for the weak derivatives (derivatives in the distribution sense):

It is well known the space above is a Sobolev space and hence it is a complete space as it can be revisited by the reader in Rudin, 1974 and Leoni, 2017.
Now we are in the position to prove Proposition 4.3.

In equation (7), the second term accounts for the training with respect to ∆, mathematically the shape of the function.

Before delving into the procedure of building a fixed basis and how it compares with a variable basis, an illustration of an application of Proposition 4.4 is contemplated in the following example.
5 Example: Digital Options
Example 5.1 In this example, let’s verify proposition 4.4 in an application in digital options The aim is to compute ∆. A digital option is a form of option that allows traders to manually set a strike price. The digital option provides traders with a fixed payout in the case when the market price of the underlying asset exceeds the strike price.
So the pay-off function can be written as:
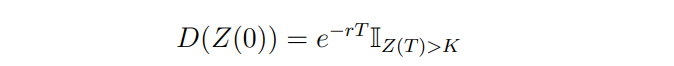
where K is the strike price, settled upon the celebration of the contract. Without loss of generality, assume that r = 0, then:
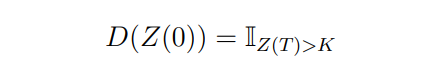
Taking the derivative inside the expectation :
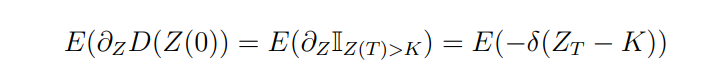
here it was used in the last step, that a weak derivative of a heavy side function is the Dirac delta. Considering the distribution density to be f, whose cumulative distribution is expressed by F, then:
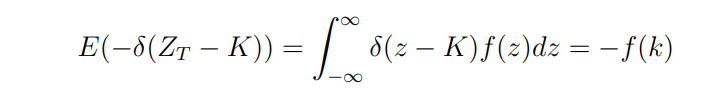
Going the other way around:
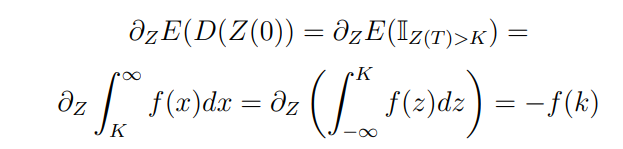
Then, it can be concluded that:
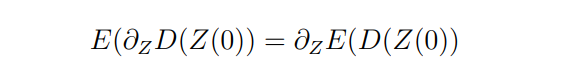
Now, a question could be posed, on how the differential labels can be found. According to this example insofar, we would need to know a priori the density f. However, in a scenario where we are presented with data, and not a simulation, an estimator of the expectation of the delta Dirac function on a sample would need to be found. Since delta Dirac would be infinite on a single point, an approximation can be considered. See in Jones, 1966 that the delta Dirac integral over a test function or a good function is :
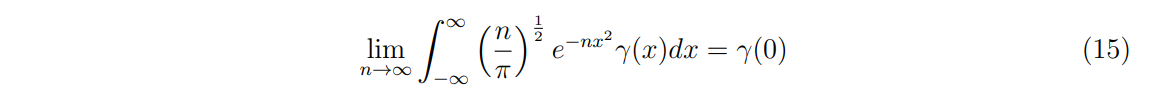
Choosing a large N
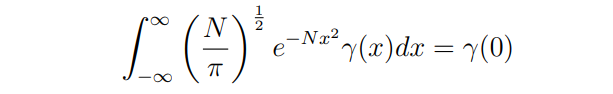
we finally get an integral we can discretize by the usual numerical methods. This procedure can be applied to any pay-off function, hence to any derivative product, solving the problem in Broadie and Glasserman, 1996.
:::info
Author:
(1) Pedro Duarte Gomes, Department of Mathematics, University of Copenhagen.
:::
:::info
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
:::