:::info
Authors:
(1) Kaier Liang, with the Mechanical Engineering and Mechanics Department at Lehigh University, PA, USA;
(2) Cristian-Ioan Vasile, with the Mechanical Engineering and Mechanics Department at Lehigh University, PA, USA.
:::
Table of Links
Abstract and I. Introduction
II. Preliminaries
III. Problem Formulation
IV. Solution
V. Simulation
VI. Conclusions and References
III. PROBLEM FORMULATION
In this section, we formulate the fair mobility-on-demand problem with requests expressed as scLTL specifications. The objective is to sequentially generate assignments for incoming scLTL requests to a fleet of vehicles, with the goal of minimizing the total travel time and ensuring fairness among the fleet of vehicles.
A. Vehicle, Environment, and Request Models

This problem can be solved using centralized methods such as optimization techniques [25], [26]. However, centralized approaches may not be able to handle disruptions well in real-time, e.g., vehicles entering and leaving the system and changes in the environment and requests. These issues are compounded by the need to collect information into a central node for decision making which may lead to delays. Moreover, for vehicle-request problems, each vehicle usually makes individual choices, and vehicles may not be willing to disclose the information to others. Therefore, in this paper, we seek distributed assignment methods that avoid the need for centralized data collection.
We assume that all agents can communicate with each other, e.g., via broadcasting to the entire fleet or a subgroup of vehicles. In this paper, a distributed assignment Asgt at time t is defined as a assignment function computed by each vehicle based on messages exchanged with other vehicles, and no vehicle takes a special role in decision-making and coordination.

B. Fairness
For vehicle assignment problems, the serving rate or customer satisfaction is a crucial factor. However, it is equally important to consider drivers’ viewpoints in terms of the fairness of allocating requests. The utility for a vehicle v for a given time period h is the sum of the onboard passengers:
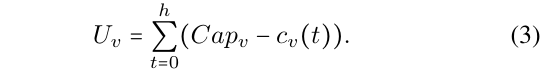
Vehicles’ utilities may vary greatly over the service horizon H. Thus, it is important to ensure fair assignment of requests while maintaining good overall performance of the fleet in terms of the total travel time for requests satisfaction J.
There are different criteria to quantify fairness, such as envy-free fairness, max-min fairness, and proportionality fairness [27]. In this paper, we use the max-min utility and deviation of utility as the two quantities to measure the fairness of the vehicles.
The max-min fairness criterion emphasizes the maximization of the least utility that a vehicle obtains, i.e., it captures the lower bound or the worst case of utility. This criterion is widely used in many applications [28]. The deviation of the utility fairness criterion, on the other hand, captures the utility distribution from the perspective of the entire group, as it directly reflects the utility spread among all vehicles.
In the vehicle assignment scenario, multiple factors can contribute to significantly uneven utility results. Vehicles’ location in the road network impacts their chances of picking up requests due to spatial and temporal variations of requests’ arrival. Secondly, differences in utility between requests and their limited number can lead to some vehicles servicing high utility requests while others are assigned lower utility ones or not at all. This may happen even in the case of a uniform probability distribution of requests over space and time.
The first case, due to spatial and temporal variation, rebalancing strategies can be used to mitigate the effects of request arrival differences over the road network. Rebalancing works by moving idle vehicles to another location to increase their chances of being assigned requests.

Summary of the approach.
For a fixed time sample interval, we conduct an auction for each active request to available vehicles. First, we construct product automata between the motion model (road network) of a vehicle and the DFAs corresponding to the requests. The route is then computed via the shortest path method (e.g., Dijkstra algorithm) applied on the product automaton graph and projection onto the motion model. If the maximum waiting and delay time is permissible, we allow the vehicles to generate the bid for the requests. After assigning the requests to the vehicles based on the auction results, we conduct a rebalancing for each idle vehicle to move vehicles to more ideal locations.
:::info
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
:::









