:::info
Authors:
(1) Haolong Li, Tongji Universiy and work done during internship at ByteDance ([email protected]);
(2) Yu Ma, Seed Foundation, ByteDance ([email protected]);
(3) Yinqi Zhang, East China Normal University and work done during internship at ByteDance ([email protected]);
(4) Chen Ye (Corresponding Author), ESSC Lab, Tongji Universiy ([email protected]);
(5) Jie Chen, Seed Foundation, ByteDance and a Project Leader ([email protected]).
:::
Table of Links
Abstract and 1 Introduction
2 Problem Definition
2.1 Arithmetical Puzzle Problem
2.2 Data Synthesizing
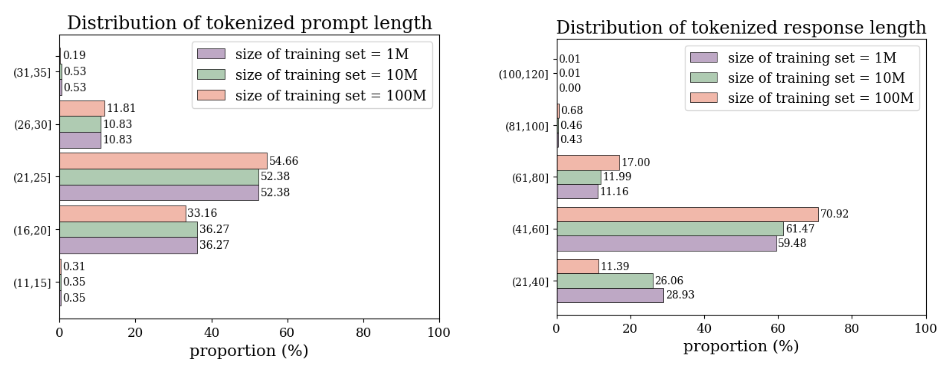
2.3 Dataset
3 Model
4 Experiments
4.1 Evaluation
4.2 Results
4.3 Case Studies
5 Conclusion and Acknowledgements
6 Limitations
7 Ethics Statement and References
A Appendix
A.1 Hyperparameter Settings
A.2 Evaluation of the Base Model
A.3 Case Study
A.4 Visualization of the Proposed Puzzle
4.1 Evaluation
For the fine-tuned model, we use the greedy decoding strategy in a zero-shot setting to generate responses. To measure the model’s performance on the proposed puzzle, a corresponding verifier is designed to automatically evaluate the correctness of the responses. Specifically, a solution is deemed correct if it satisfies the following rules:
• No extra or illegal characters.
• There are only N − 1 equations and all the corresponding calculations are correct.
• F(X1, . . . , XN | ops) = T.
• All {Xi | i ∈ {1, 2, . . . , N}} and the intermediate calculation results are only used once.
The detailed steps of evaluating the solution for this puzzle is described in Algorithm 2.
4.2 Results
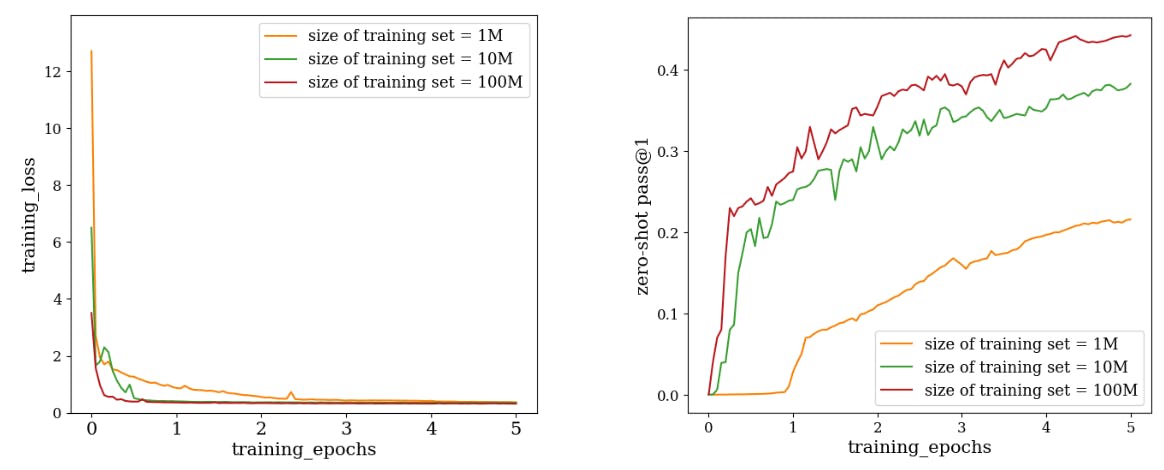
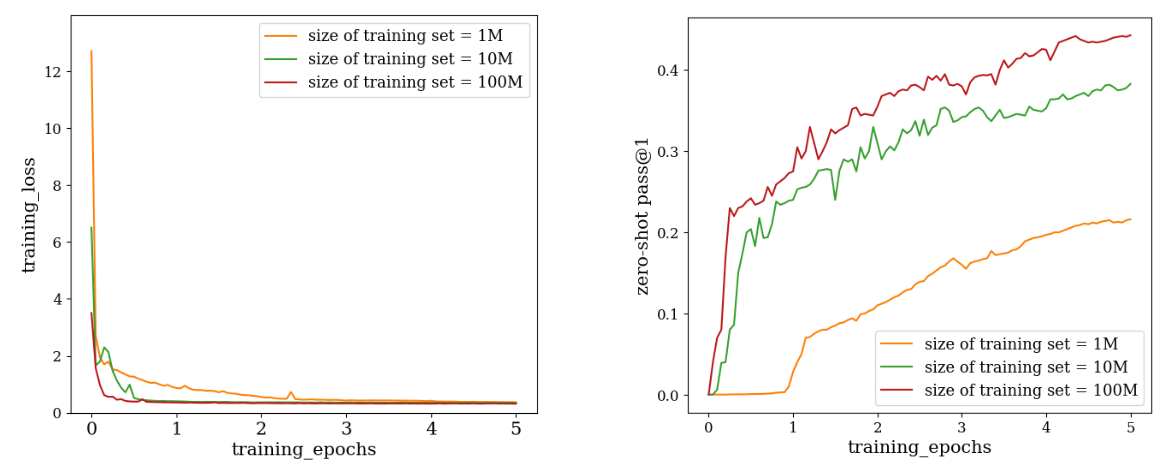
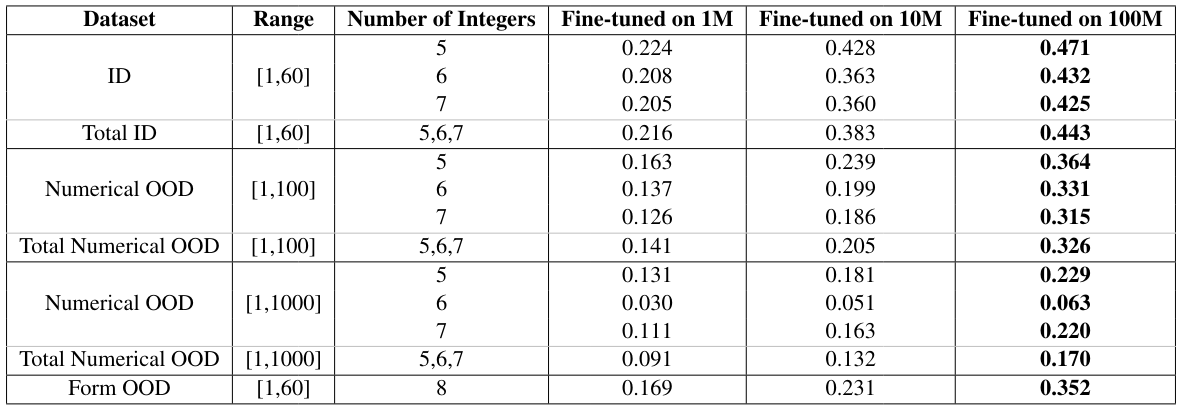
As mentioned in Section 2.3, we have generated three training datasets with different sizes to explore the data scaling effects on the fine-tuned model. The pass@1 rate on different in-distribution and out-of-distribution test datasets are shown in Table 2. When the model is fine-tuned with 100M samples, it achieves the highest score with a zero-shot pass@1 of 0.44 in the in-distribution test dataset, and 0.33 and 0.35 in the two OOD datasets, respectively.
Furthermore, we have shown the training curves of the model fine-tuned on these three datasets in Figure 3. From Figure 3, a faster decaying rate is clearly observed in the training loss when increasing the training data size, which is consistent with the rapid increase of the pass@1 rate evaluated on the in-distribution dataset. The same enhancement of the performance also occurs in the two OOD test datasets as shown in Table 2.
Additionally, we have also conducted tests of this puzzle on the base model (open-llama-3B) and several other open-source and closed-source models with both few-shot and CoT prompting. The results and some of the generated cases are shown in Appendix A.2, demonstrating the necessity of fine-tuning with regard to solving such puzzle problems.
4.3 Case Studies
We further demonstrate the different solutions provided by models trained with 1M / 10M / 100M training data on the form OOD test dataset for several challenging queries. As shown in Figure 4 in Appendix A.3, the model trained on 1M samples is still limited to a fixed number of reasoning steps, whereas the models trained on 10M / 100M samples exhibit a higher-level understanding of the problem and perform an adequate number of reasoning steps. However, compared to the model trained on 100M samples, the model trained on 10M samples may still encounter computational or logical errors in the final step of reasoning.
:::info
This paper is available on arxiv under CC BY-NC-SA 4.0 Deed (Attribution-Noncommercial-Sharelike 4.0 International) license.
:::