Table of Links
- Prologue
- Diagrammatic(s) Rules
- Straight-forward Eikonal
- Legacy Bosonization
- Wonton Holography
- Holographic Propagators
- Strange Cuprates
- Stranger Things
- Epilogue
Holographic Propagators
The early holographic studies of fermion propagators [28] produced a number of intriguing results, including multiple Fermi surfaces (which merge into one critical ’Fermi ball’ in some extreme limits), dispersionless poles, and oscillatory frequency dependence (which was later shown not to arise in more systematic ’top down’ constructions [26]), etc. A physical interpretation of those results is impeded by the fact that much of this work is numerical.
A simple and amenable to analytical treatment semiclassical calculation can be performed in the regime mL ≫ 1 where m is a mass of the conjectured dual bulk fermion [28, 29]. In this regime, the fermion’s paths contributing to various quantum-mechanical amplitudes follow closely the classical boundary-to-boundary trajectories (geodesics) derived from the (imaginary-time) action
by varying over τ(u) and r(u).
Evaluating this action on its geodesic one obtains

While an explicit analytic computation of (29) can only be performed in some special cases, the one-parameter space/time dependencies can be readily found for a broad variety of metrics. Specifically, for the HV metric (26) one obtains [29, 30]
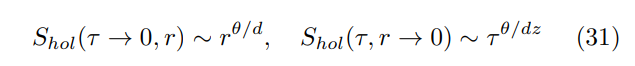
Notably, in the absence of hyperscaling violation (θ = 0) both these asymptotics become either constant (less likely) or logarithmic (more likely, see below). Thus, if the classical EMD Lagrangian (22) were to represent a valid bulk dual of a boundary theory with the gauge-like interaction (1) the asymptotics (31) would not be readily reconcilable with the eikonal/bosonization results (11,21) which depend primarily on z (via η) rather than θ.

and is composed of the two independent solutions which read

Imposing the proper boundary conditions and following the holographic dictionary [26] one then defines the propagator as a reflection coefficient for the wave incident at the boundary

A different behavior (unattainable in the case of a HV metric (26) with finite z and θ) occurs for α = β + 1 in which case the integral in (33) diverges at u → 0. This peculiar NFL regime, dubbed ’local criticality’, is characterized by the propagator
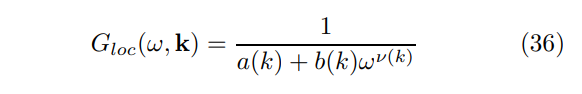
where a(k), b(k), and ν(k) ∼ k are non-singular functions of momentum that can, in general, produce multiple poles identified as the distinct (’fractionalized’) FS [28].
Fourier transforming (36) is complicated by the fact that G(ω, k) is not analytically known across the entire range of its arguments. However, the fast (and/or furious) Fourier transformation via a saddle point suggests the following form of this function in the spacetime domain

Adding to the intrigue, there are some recent Monte Carlo results on the 2d Hubbard and t − J models that have long been thought to represent the prototypical NFL normal state in the cuprates. These results do not readily conform to a momentum-independent, yet strongly energy-dependent, self-energy function, showing less of energy/temperature dependence than any of the above expressions [33]. It remains to be seen as to what this might imply for the general applicability of the theories of fermions (’spinons’) governed by the interactions (1) to the analysis of those microscopic models.
:::info
Author:
(1) D. V. Khveshchenko, Department of Physics and Astronomy, University of North Carolina, Chapel Hill, NC 27599.
:::
:::info
This paper is available on arxiv under CC BY 4.0 DEED license.
:::