Table of Links
Abstract and 1. Introduction
-
Related Works
-
Convex Relaxation Techniques for Hyperbolic SVMs
3.1 Preliminaries
3.2 Original Formulation of the HSVM
3.3 Semidefinite Formulation
3.4 Moment-Sum-of-Squares Relaxation
-
Experiments
4.1 Synthetic Dataset
4.2 Real Dataset
-
Discussions, Acknowledgements, and References
A. Proofs
B. Solution Extraction in Relaxed Formulation
C. On Moment Sum-of-Squares Relaxation Hierarchy
D. Platt Scaling [31]
E. Detailed Experimental Results
F. Robust Hyperbolic Support Vector Machine
E Detailed Experimental Results
E.1 Visualizing Decision Boundaries
Here we visualize the decision boundary of for PGD, SDP relaxation and sparse moment-sum-ofsquares relaxation (Moment) on one fold of the training to provide qualitative judgements.
We first visualize training on the first fold for Gaussian 1 dataset from Figure 3 in Figure 5. We mark the train set with circles and test set with triangles, and color the decision boundary obtained by three methods with different colors. In this case, note that SDP and Moment overlap and give identical decision boundary up to machine precision, but they are different from the decision boundary of PGD method. This slight visual difference causes the performance difference displayed in Table 1.
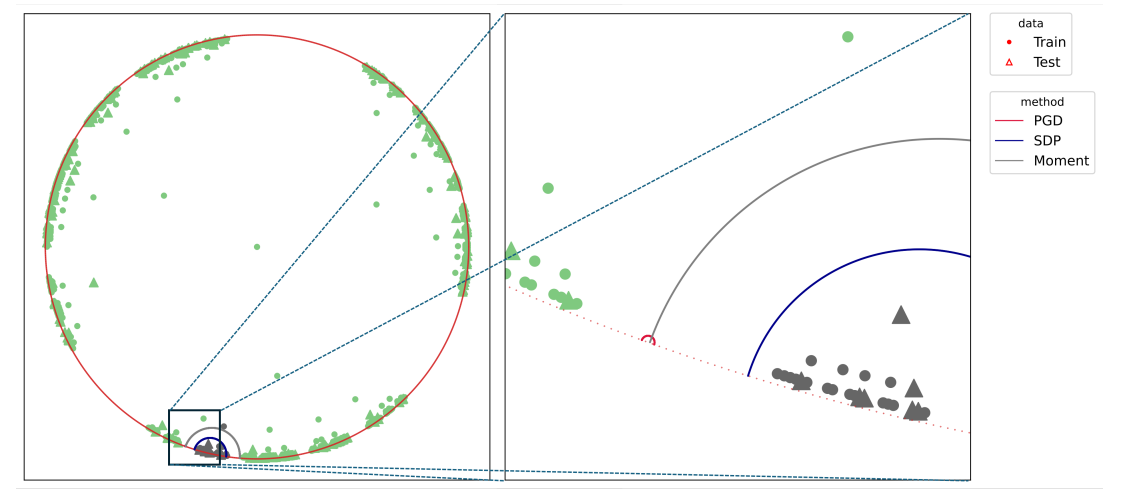
We next visualize the decision boundary for tree 2 from Figure 3 in Figure 6. Here the difference is dramatic: we visualize both the entire data in the left panel and the zoomed-in one on the right. We indeed observe that the decision boundary from moment-sum-of-squares relaxation have roughly equal distance from points to the grey class and to the green class, while SDP relaxation is suboptimal in that regard but still enclosing the entire grey region. PGD, however, converges to a very poor local minimum that has a very small radius enclosing no data and thus would simply classify all data sample to the same class, since all data falls to one side of the decision
boundary. As commented in Section 4, data imbalance is to blame, in which case the final converged solution is very sensitive to the choice of initialization and other hyperparameters such as learning rate. This is in stark contrast with solving problems using the interior point method, where after implementing into MOSEK, we are essentially care-free. From this example, we see that empirically sparse moment-sum-of-squares relaxation finds linear separator of the best quality, particularly in cases where PGD is expected to fail.
E.2 Synthetic Gaussian
To generate mixture of Gaussian in hyperbolic space, we first generate them in Euclidean space, with the center coordinates independently drawn from a standard normal distribution. 𝐾 such centers are drawn for defining 𝐾 different classes. Then we sample isotropic Gaussian at respective center with scale 𝑠. Finally, we lift the generated Gaussian mixtures to hyperbolic spaces using exp0 . For simplicity, we only present results for the extreme values: 𝐾 ∈ {2, 5}, 𝑠 ∈ {0.4, 1}, and 𝐶 ∈ {0.1, 10}.
For each method (PGD, SDP, Moment), we compute the train/test accuracy, weighted F1 score, and loss on each of the 5 folds of data for a specific (𝐾, 𝑠, 𝐶) configuration. We then average these metrics across the 5 folds, for all methods and configurations. To illustrate the performance, we plot the improvements of the average metrics of the Moment and SDP methods compared to PGD as bar plots for 15 different seeds. Outliers beyond the interquartile range (Q1 and Q3) are excluded for clarity, and a zero horizontal line is marked for reference. Additionally, to compare the Moment and SDP methods, we compute the average optimality gaps similarly, defined in Equation (15), and present them as bar plots. Our analysis begins by examining the train/test accuracy and weighted F1 score of the PGD, SDP, and Moment methods across various synthetic Gaussian configurations, as shown in Figures 7 to 10.
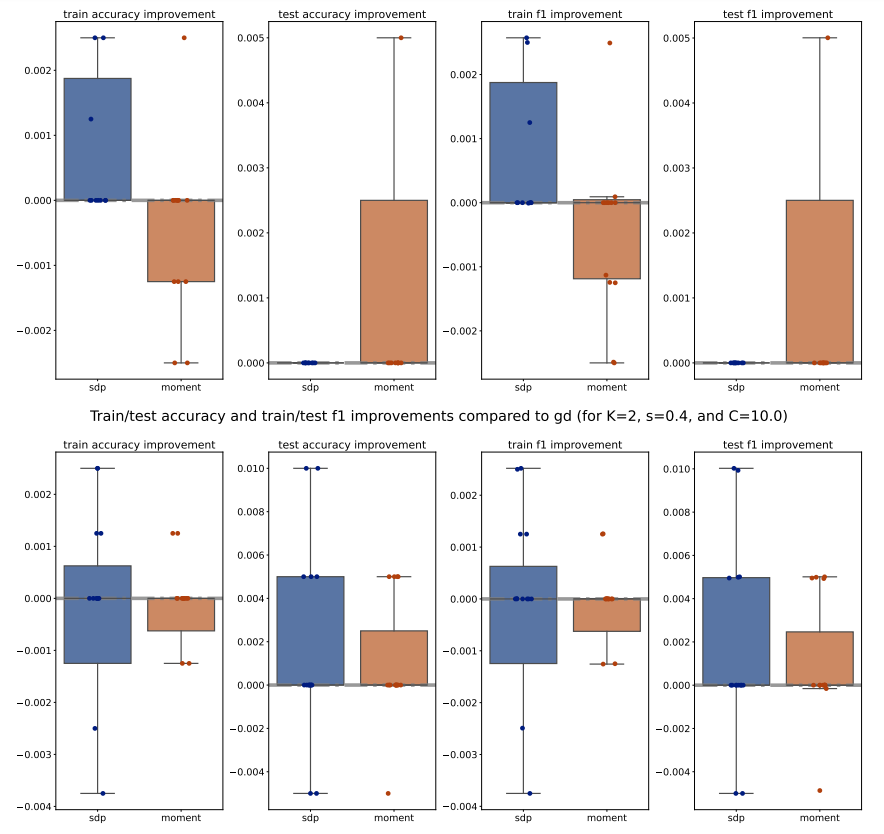
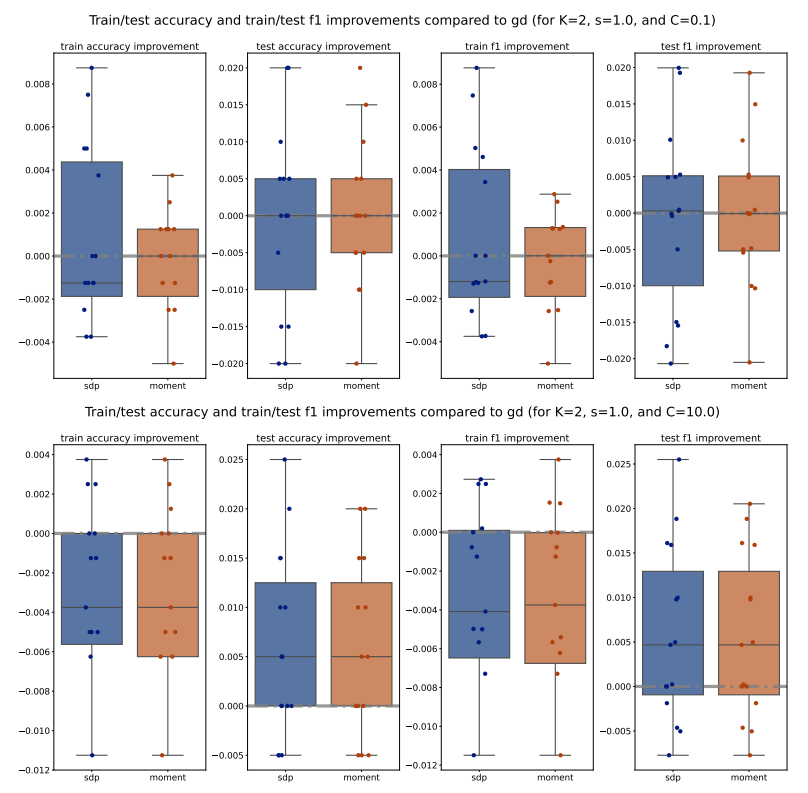
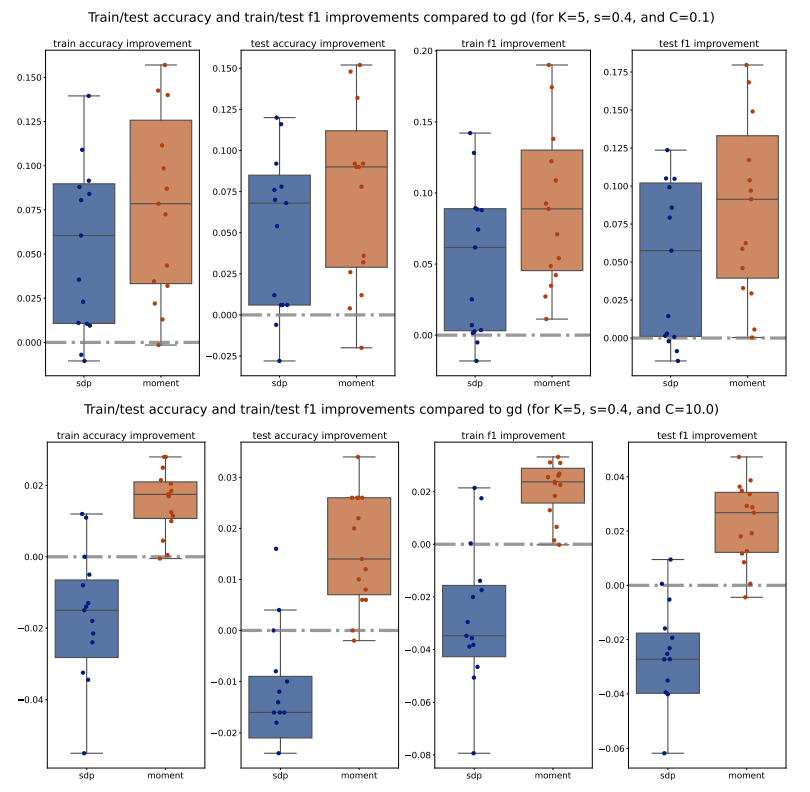
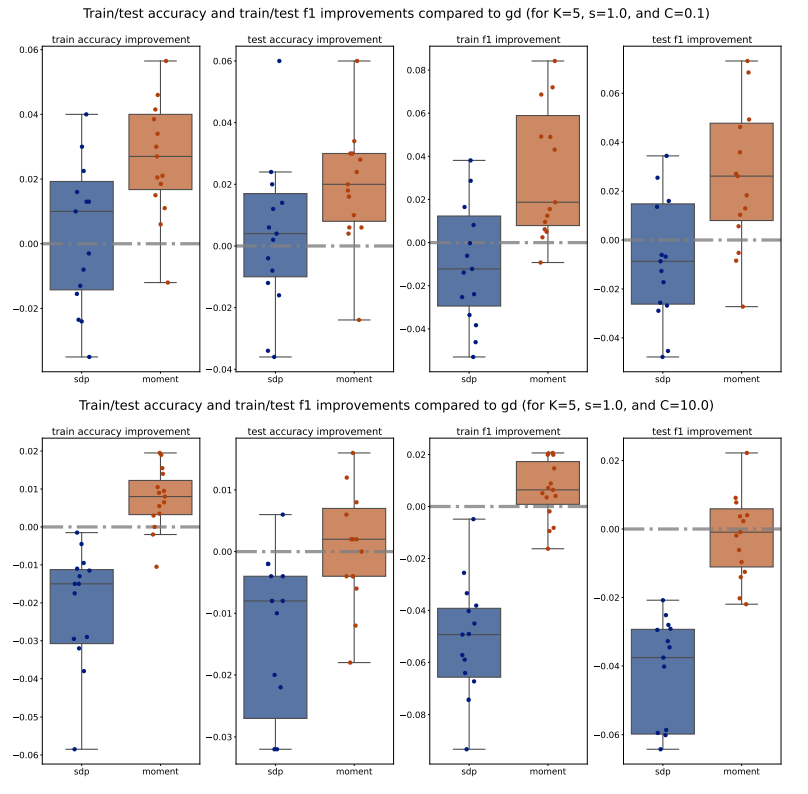
Across various configurations, we observe that both the Moment and SDP methods generally show improvements over PGD in terms of train and test accuracy as well as weighted F1 score. Notably, we observe that Moment method often shows more consistent improvements compared to SDP. This consistency is evident across different values of (𝐾, 𝑠, 𝐶), suggesting that the Moment method is more robust and provide more generalizable decision boundaries. Moreover, we observe that 1. for larger number of classes (i.e. larger 𝐾), the Moment method consistently and significantly outperforms both SDP and PGD, highlighting its capability to manage complex class structures efficiently; and 2. for simpler datasets (with smaller scale 𝑠), both Moment and SDP methods generally outperform PGD, where the Moment method particularly shows a promising performance advantage over both PGD and SDP.
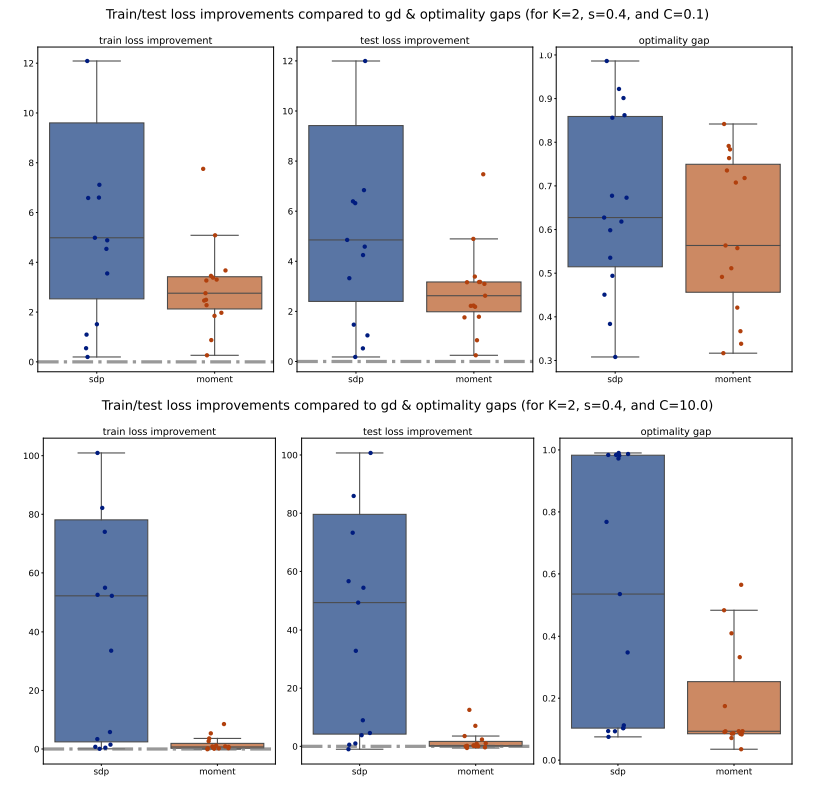
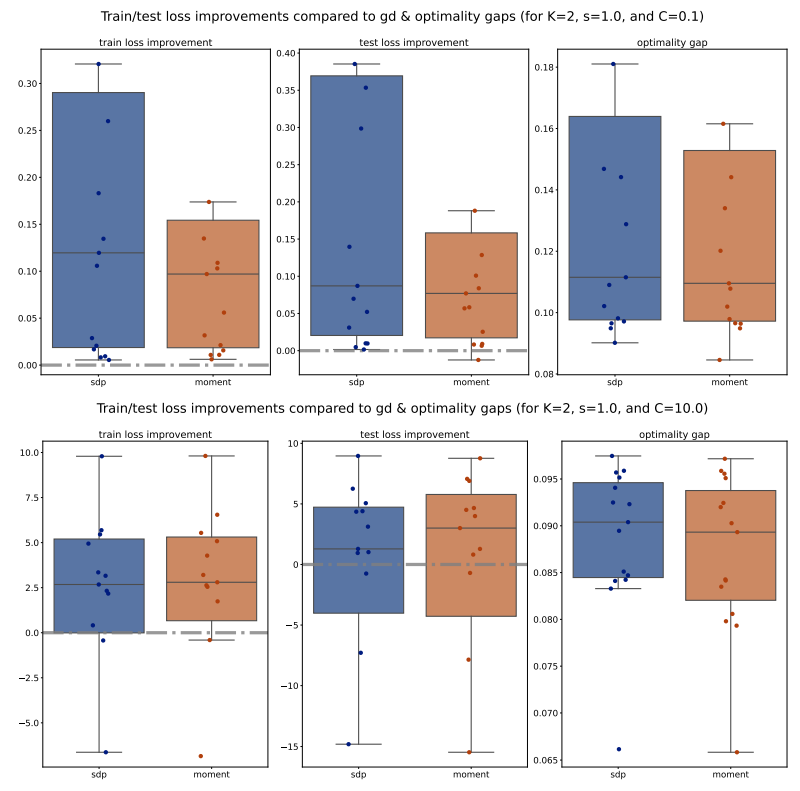
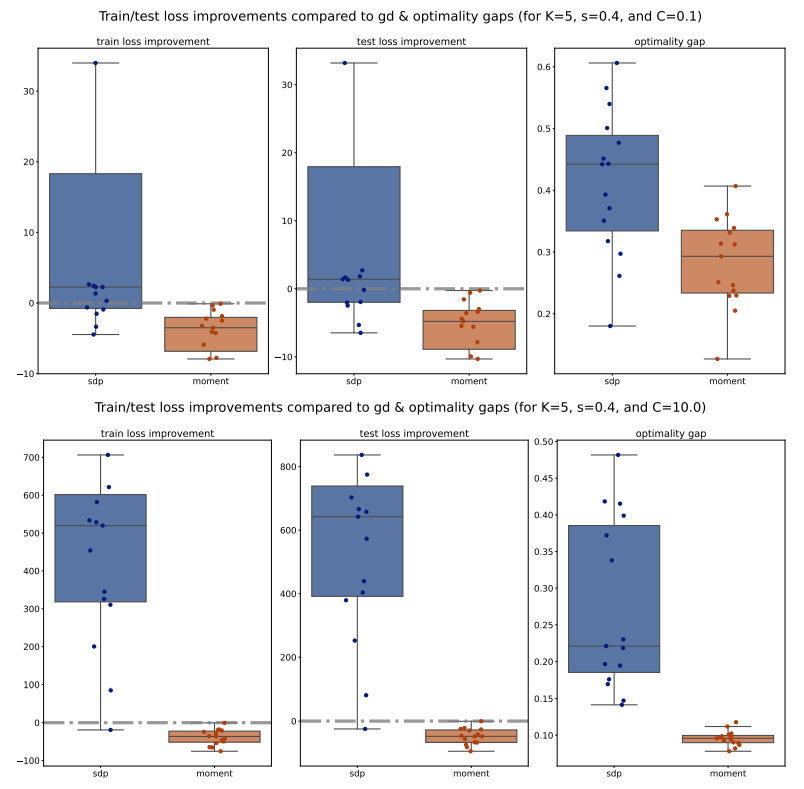
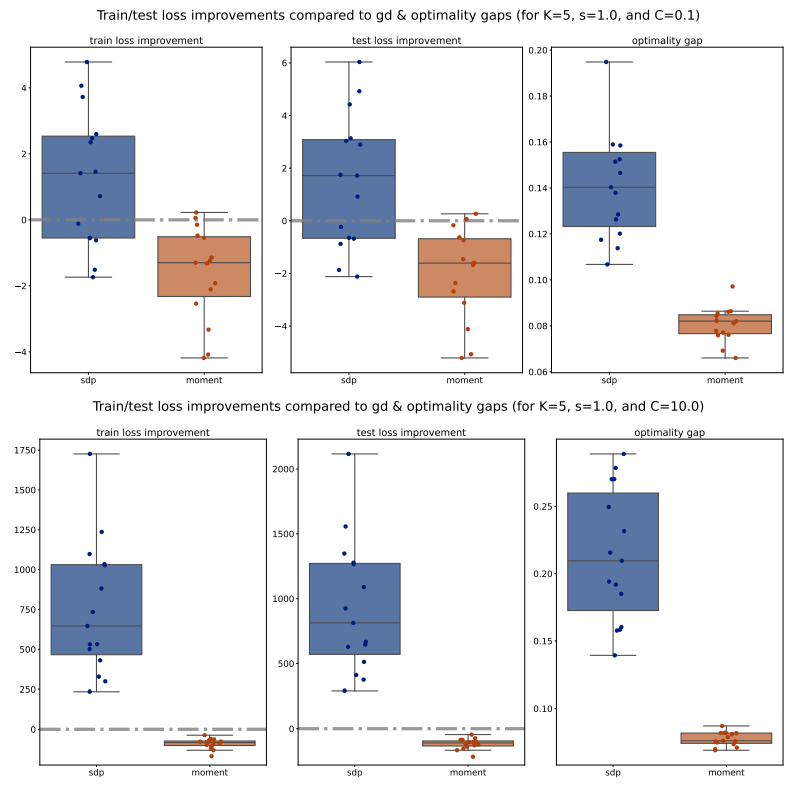
Next, we move to examine the train/test loss improvements compared to PGD and optimality gaps comparison across various configurations, shown in Figures 11 to 14. We observe that for 𝐾 = 5, the Moment method achieves significantly smaller losses compared to both PGD and SDP, which aligns with our previous observations on accuracy and weighted F1 scores. However, for 𝐾 = 2, the losses of the Moment and SDP methods are generally larger than PGD’s. Nevertheless, it is important to note that these losses are not direct measurements of our optimization methods’ quality; rather, they measure the quality of the extracted solutions. Therefore, a larger loss does not necessarily imply that our optimization methods are inferior to PGD, as the heuristic extraction methods might significantly impact the loss. Additionally, we observe that the optimality gaps of the Moment method are significantly smaller than those of the SDP method, suggesting that Moment provides better solutions. Interestingly, the optimality gaps of the Moment method also exhibit smaller variance compared to SDP, as indicated by the smaller boxes in the box plots, further supporting the consistency and robustness of the Moment method.
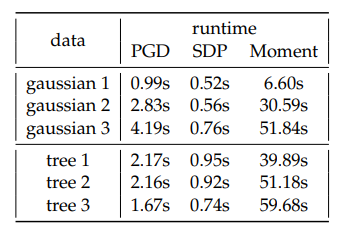
Lastly, we compare the computational efficiency of these methods, where we compute the average runtime to finish 1 fold of training for each model on synthetic dataset, shown in Table 4. We observe that sparse moment relaxation typically requires at least one order of magnitude in runtime compared to other methods, which to some extent limits the applicability of this method to large scale dataset.
E.3 Real Data
In this section we provide detailed performance breakdown by the choice of regularization 𝐶 for both one-vs-one and one-vs-rest scheme in Tables 5 to 10.
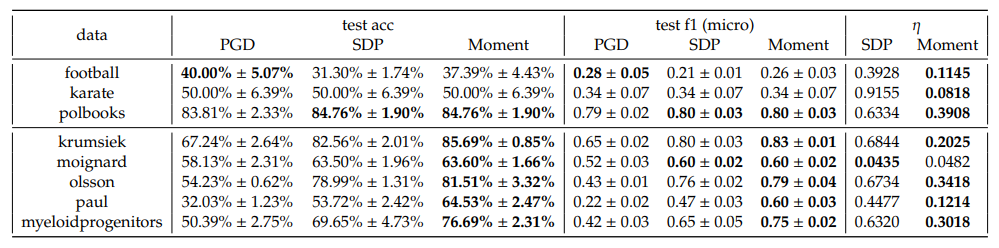
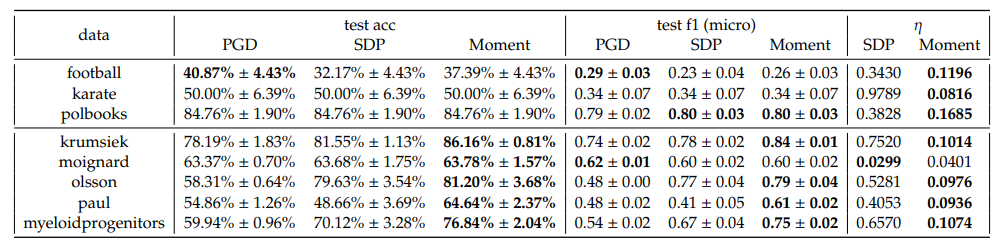
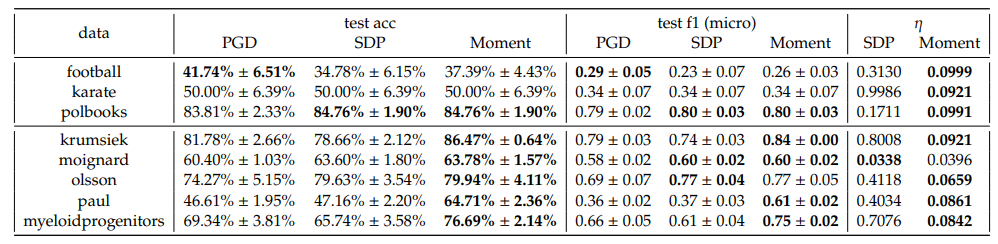
In one-vs-rest scheme, we observe that the Moment method consistently outperforms both PGD and SDP across almost all datasets and 𝐶 in terms of accuracy and F1 scores. Notably, the optimality gaps, 𝜂, for Moment are consistently lower than those for SDP, indicating that the Moment method’s solution obtain a better gap, which underscore the effectiveness of the Moment method in real datasets.
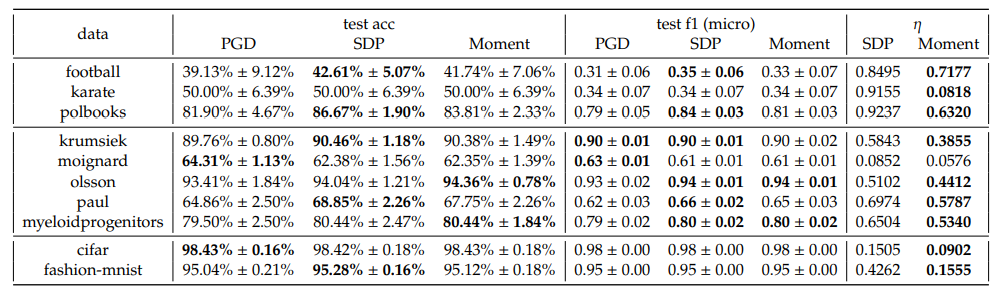
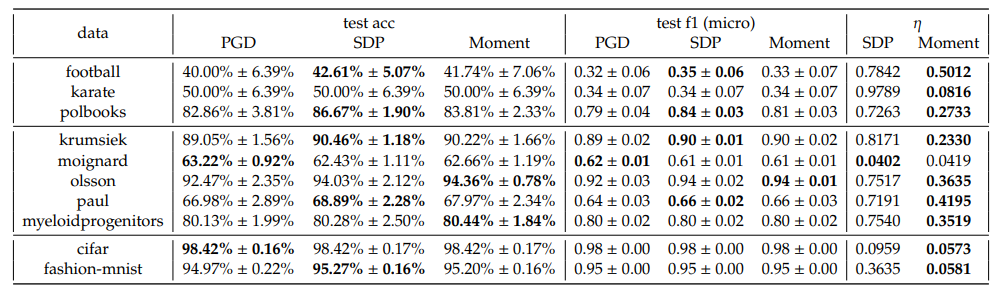
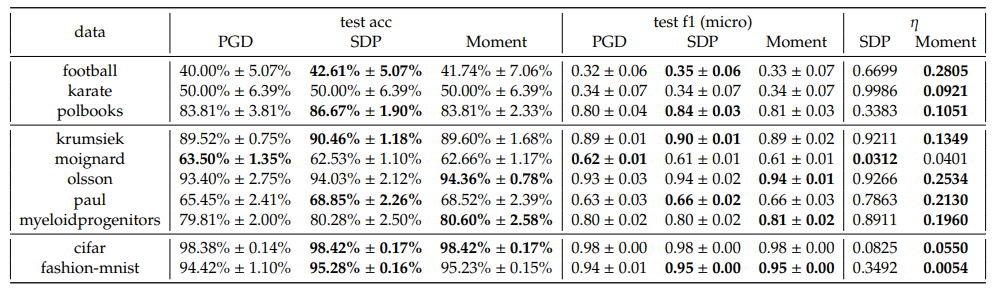
In one-vs-one scheme however, we observe that the SDP and Moment have comparative performances, both better than PGD. Nevertheless, the optimality gaps of SDP are still significantly larger than the Moment’s, for almost all cases.
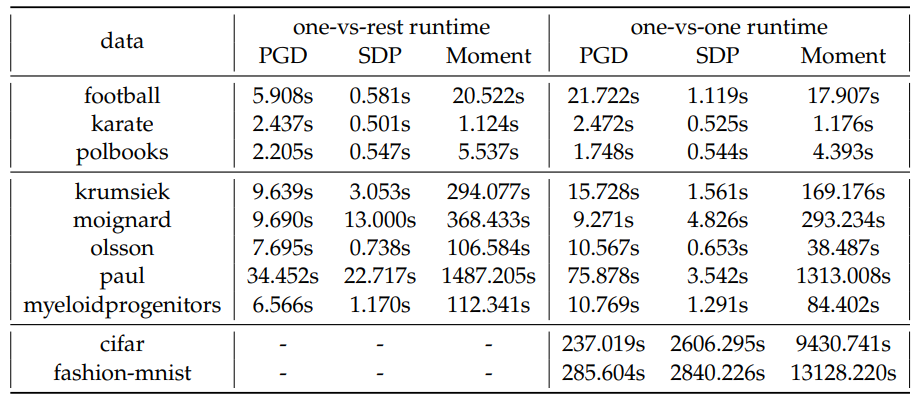
Similarly, we compare the average runtime to finish 1 fold of training for each model on these real datasets, shown in Table 11. We observe a similar trend: the sparse moment relaxation typically requires at least an order of magnitude more runtime compared to the other methods.
:::info
Authors:
(1) Sheng Yang, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA ([email protected]);
(2) Peihan Liu, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA ([email protected]);
(3) Cengiz Pehlevan, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, Center for Brain Science, Harvard University, Cambridge, MA, and Kempner Institute for the Study of Natural and Artificial Intelligence, Harvard University, Cambridge, MA ([email protected]).
:::
:::info
This paper is available on arxiv under CC by-SA 4.0 Deed (Attribution-Sharealike 4.0 International) license.
:::