Table of Links
Abstract and I. Introduction
II. Related Works
III. Dead Reckoning using Radar Odometry
IV. Stochastic Cloning Indirect Extended Kalman Filter
V. Experiments
VI. Conclusion and References
V. EXPERIMENTS
A. Open-source datasets
ts To verify the proposed DeRO algorithm, five open source datasets provided by [23] was used, namely Carried 1 to 5. Here, we briefly describe overview of the datasets; for more detailed information about the setup, readers are encouraged to refer to the mentioned paper. These datasets were recorded in an office building using a hand-held sensor platform equipped with a 4D milimeter-wave FMCW radar (TI IWR6843AOP) and an IMU (Analog Devices ADIS16448). The IMU provides data at approximately 400 Hz, while the radar captures 4D point clouds at 10 Hz. In addition, the radar has a FOV of 120 deg for both azimuth
or elevation angles. Furthermore, the sensor platform includes a monocular camera, which is utilized to generate a pseudo ground truth via the visual inertial navigation system (VINS) algorithm with loop closure. It is worth noting that although the IMU also provides barometric measurements, we did not utilize them.

B. Evaluation
For evaluation purposes, we aligned the estimated trajectories with the pseudo ground truth using the method described in [33], employing position-yaw alignment. This tool also calculates the Absolute Trajectory Error (ATE) metric, as defined in [34], which we will utilize for comparison.
1) Evaluation of 2D Trajectory: Figure 3 illustrates the top-view of the aligned X-Y trajectory estimates obtained by
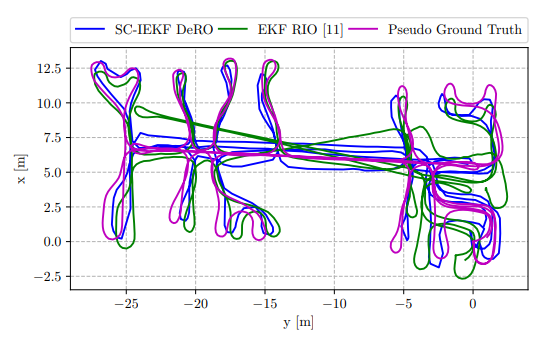
the EKF RIO and SC-IEKF DeRO. Overall, Both methods demonstrate decent estimation performance. However, our proposed method exhibits superior performance, particularly evident when the sensor platform traces a straight loop from (x, y) = (7, 0) to (x, y) = (7, −25). Furthermore, as the start and end points of the trajectory coincide, we can relatively judge the filter’s accuracy solely by examining the final estimated positions. Specifically, SC-IEKF yields an approximate position of (ˆx, y, ˆ zˆ) = (−0.82, −0.84, 0.23), while EKF RIO yields approximately (5.49, −1.42, 1.71), corresponding to distance errors of approximately 1.2 m and 5.9 m, respectively. Thus, our proposed method reduces the final position distance error from the conventional approach by approximately 79.6%.
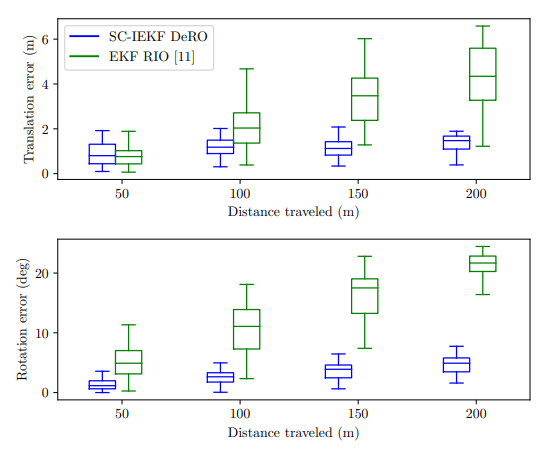
2) Evaluation of Relative Errors: The relative errors in terms of translation and rotation are depicted in Fig. 4 using boxplots. Our method consistently outperforms the EKF RIO in both categories. Although the translation error boxplot shows a slightly larger error and uncertainty for the SCIEKF DeRO after the sensor platform travels 50 m compared to its competitor, the EKF RIO exhibits rapid position drift at distances of {100, 150, 200} m, whereas our proposed method maintains an acceptable error level from start to finish. This trend is also evident in the rotation error plot.
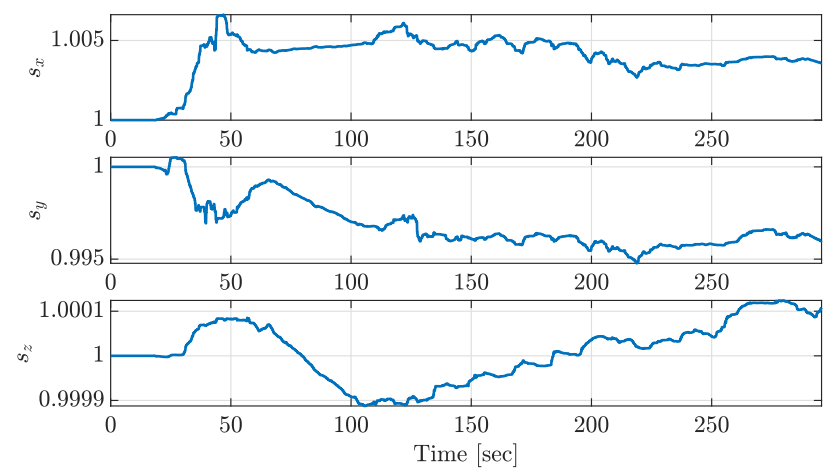
Fig. 5 reports the radar scale factor estimation obtained using the presented approach. From the plot, it is evident that the scale factor along the x-axis tends to converge and stabilize at 1.005, while it stabilizes at 0.995 along the y-axis, and approximately 1 with small fluctuations along the z-axis. This observation, coupled with the analysis of the estimation results, supports our belief that compensating for radar scale factor is crucial and can lead to significant improvements.
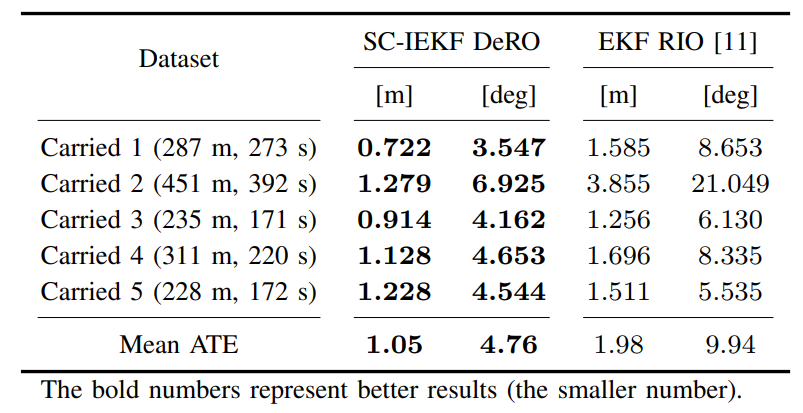
3) Evaluation of ATE: Table I summarizes the ATE in terms of both translation and rotation for the two considered algorithms across all datasets. Once again, the SC-IEKF DeRO completely outperforms the EKF RIO in all trials, especially in the Carried 1 and 2 datasets, which features numerous turns. For instance, in the Carried 2 field test (the longest trajectory with 451 m distance and 392 seconds duration), our developed method yields a translation error of 1.279 m and rotation error of 6.925 deg, compared to 3.855 m and 21.049 deg for the EKF RIO. This represents a translation error reduction of 66.8% and a rotation error reduction of 67.1%. Overall, across the mean ATE of the five experiments, our DeRO approach reduces the translation error by approximately 47% and the rotation error by 52%.
VI. CONCLUSION
In this article, we have proposed DeRO, a framework of dead reckoning based on radar odometry with tilt angle measurements from accelerometer. In contrast to the previous studies where radar measurements are used solely to update the estimations, we employ the 4D FMCW radar as a hybrid component of our system. Specifically, we leverage Doppler velocity obtained by the RANSAC/LSQ algorithm with gyroscope measurements to primarily perform dead reckoning (calculating poses). The radar’s range measurements, in conjunction with accelerometer data, are utilized for the filter’s measurement update. This approach enables estimation and compensation of Doppler velocity scale factor errors, while also allowing for compensation of linear acceleration from accelerometers using radar velocity estimation. Moreover, we apply the renowned stochastic cloning-based IEKF to address relative distance problem obtained from the scan matching. The effectiveness of our proposed method is validated through a comprehensive evaluation using a set of open-source datasets. As expected, directly utilizing radar velocity instead of integrating acceleration offers a significantly improved odometry solution. The provided mean ATE across all test fields demonstrates that SC-IEKF DeRO achieves substantially better overall performance compared to its competitor. One limitation of this study is that the DeRO approach operates at a relatively slow rate due to the radar component. Addressing this limitation will be a focus of our future research.
REFERENCES
[1] P. Groves, Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems, Second Edition. Artech, 2013.
[2] S. Nassar, X. Niu, and N. El-Sheimy, “Land-vehicle ins/gps accurate positioning during gps signal blockage periods,” Journal of Surveying Engineering, vol. 133, no. 3, pp. 134–143, 2007.
[3] G. Huang, “Visual-inertial navigation: A concise review,” in 2019 International Conference on Robotics and Automation (ICRA), 2019, pp. 9572–9582.
[4] T. Shan, B. Englot, D. Meyers, W. Wang, C. Ratti, and R. Daniela, “Lio-sam: Tightly-coupled lidar inertial odometry via smoothing and mapping,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2020, pp. 5135–5142.
[5] J. Jiang, X. Chen, W. Dai, Z. Gao, and Y. Zhang, “Thermal-inertial slam for the environments with challenging illumination,” IEEE Robotics and Automation Letters, vol. 7, no. 4, pp. 8767–8774, 2022.
[6] M. Bijelic, T. Gruber, and W. Ritter, “A benchmark for lidar sensors in fog: Is detection breaking down?” in 2018 IEEE Intelligent Vehicles Symposium (IV). IEEE, 2018, p. 760–767.
[7] A. Venon, Y. Dupuis, P. Vasseur, and P. Merriaux, “Millimeter wave fmcw radars for perception, recognition and localization in automotive applications: A survey,” IEEE Transactions on Intelligent Vehicles, vol. 7, no. 3, pp. 533–555, 2022.
[8] Z. Han, J. Wang, Z. Xu, S. Yang, L. He, S. Xu, and J. Wang, “4d millimeter-wave radar in autonomous driving: A survey,” arXiv preprint arXiv:2306.04242, 2023.
[9] D. Kellner, M. Barjenbruch, J. Klappstein, J. Dickmann, and K. Dietmayer, “Instantaneous ego-motion estimation using multiple doppler radars,” in 2014 IEEE International Conference on Robotics and Automation (ICRA), 2014, pp. 1592–1597.
[10] J. Zhang, H. Zhuge, Z. Wu, G. Peng, M. Wen, Y. Liu, and D. Wang, “4dradarslam: A 4d imaging radar slam system for large-scale environments based on pose graph optimization,” in 2023 IEEE International Conference on Robotics and Automation (ICRA), 2023, pp. 8333– 8340.
[11] C. Doer and G. F. Trommer, “An ekf based approach to radar inertial odometry,” in 2020 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), 2020, pp. 152– 159.
[12] D. Titterton and J. L. Weston, Strapdown inertial navigation technology. IET, 2004, vol. 17.
[13] W. J. Park, J. W. Song, C. H. Kang, J. H. Lee, M. H. Seo, S. Y. Park, J. Y. Yeo, and C. G. Park, “Mems 3d dr/gps integrated system for land vehicle application robust to gps outages,” IEEE Access, vol. 7, pp. 73 336–73 348, 2019.
[14] S. Macenski, T. Foote, B. Gerkey, C. Lalancette, and W. Woodall, “Robot operating system 2: Design, architecture, and uses in the wild,” Science Robotics, vol. 7, no. 66, p. eabm6074, 2022.
[15] B.-H. Lee, J.-H. Song, J.-H. Im, S.-H. Im, M.-B. Heo, and G.-I. Jee, “Gps/dr error estimation for autonomous vehicle localization,” Sensors, vol. 15, no. 8, pp. 20 779–20 798, 2015.
[16] R. Guo, P. Xiao, L. Han, and X. Cheng, “Gps and dr integration for robot navigation in substation environments,” in The 2010 IEEE International Conference on Information and Automation, 2010, pp. 2009–2012.
[17] M. Sabet, H. M. Daniali, A. Fathi, and E. Alizadeh, “Experimental analysis of a low-cost dead reckoning navigation system for a land vehicle using a robust ahrs,” Robotics and Autonomous Systems, vol. 95, pp. 37–51, 2017.
[18] Z. Yu, Y. Hu, and J. Huang, “Gps/ins/odometer/dr integrated navigation system aided with vehicular dynamic characteristics for autonomous vehicle application,” IFAC-PapersOnLine, vol. 51, no. 31, pp. 936–942, 2018, 5th IFAC Conference on Engine and Powertrain Control, Simulation and Modeling E-COSM 2018.
[19] X. Yang and H. He, “Gps/dr integrated navigation system based on adaptive robust kalman filtering,” in 2008 International Conference on Microwave and Millimeter Wave Technology, vol. 4, 2008, pp. 1946– 1949.
[20] K. Takeyama, T. Machida, Y. Kojima, and N. Kubo, “Improvement of dead reckoning in urban areas through integration of low-cost multisensors,” IEEE Transactions on Intelligent Vehicles, vol. 2, no. 4, pp. 278–287, 2017.
[21] J. H. Jung, J. Cha, J. Y. Chung, T. I. Kim, M. H. Seo, S. Y. Park, J. Y. Yeo, and C. G. Park, “Monocular visual-inertial-wheel odometry using low-grade imu in urban areas,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 2, pp. 925–938, 2022.
[22] C. Doer and G. F. Trommer, “Radar inertial odometry with online calibration,” in 2020 European Navigation Conference (ENC), 2020, pp. 1–10.
[23] ——, “Yaw aided radar inertial odometry using manhattan world assumptions,” in 2021 28th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), 2021, pp. 1–9.
[24] ——, “Radar visual inertial odometry and radar thermal inertial odometry: Robust navigation even in challenging visual conditions,” in 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2021, pp. 331–338.
[25] C. Doer, J. Atman, and G. F. Trommer, “Gnss aided radar inertial odometry for uas flights in challenging conditions,” in 2022 IEEE Aerospace Conference (AeroConf, 2022.
[26] Y. Z. Ng, B. Choi, R. Tan, and L. Heng, “Continuous-time radarinertial odometry for automotive radars,” in 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2021, pp. 323–330.
[27] J. Michalczyk, R. Jung, and S. Weiss, “Tightly-coupled ekf-based radar-inertial odometry,” in 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2022, pp. 12 336–12 343.
[28] S. Roumeliotis and J. Burdick, “Stochastic cloning: a generalized framework for processing relative state measurements,” in Proceedings 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), vol. 2, 2002, pp. 1788–1795 vol.2.
[29] J. Michalczyk, R. Jung, C. Brommer, and S. Weiss, “Multi-state tightly-coupled ekf-based radar-inertial odometry with persistent landmarks,” in 2023 IEEE International Conference on Robotics and Automation (ICRA), 2023, pp. 4011–4017.
[30] Y. Almalioglu, M. Turan, C. X. Lu, N. Trigoni, and A. Markham, “Milli-rio: Ego-motion estimation with low-cost millimetre-wave radar,” IEEE Sensors Journal, vol. 21, no. 3, pp. 3314–3323, 2021.
[31] H. Chen, Y. Liu, and Y. Cheng, “Drio: Robust radar-inertial odometry in dynamic environments,” IEEE Robotics and Automation Letters, vol. 8, no. 9, pp. 5918–5925, 2023.
[32] J. Sola, “Quaternion kinematics for the error-state kalman filter,” arXiv preprint arXiv:1711.02508, 2017.
[33] Z. Zhang and D. Scaramuzza, “A tutorial on quantitative trajectory evaluation for visual(-inertial) odometry,” in 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2018, pp. 7244–7251.
[34] A. Geiger, P. Lenz, and R. Urtasun, “Are we ready for autonomous driving? the kitti vision benchmark suite,” in 2012 IEEE Conference on Computer Vision and Pattern Recognition, 2012, pp. 3354–3361.
:::info
Authors:
(1) Hoang Viet Do, Intelligent Navigation and Control Systems Laboratory (iNCSL), School of Intelligent Mechatronics Engineering, and the Department of Convergence Engineering for Intelligent Drone, Sejong University, Seoul 05006, Republic Of Korea ([email protected]);
(2) Yong Hun Kim, Intelligent Navigation and Control Systems Laboratory (iNCSL), School of Intelligent Mechatronics Engineering, and the Department of Convergence Engineering for Intelligent Drone, Sejong University, Seoul 05006, Republic Of Korea ([email protected]);
(3) Joo Han Lee, Intelligent Navigation and Control Systems Laboratory (iNCSL), School of Intelligent Mechatronics Engineering, and the Department of Convergence Engineering for Intelligent Drone, Sejong University, Seoul 05006, Republic Of Korea ([email protected]);
(4) Min Ho Lee, Intelligent Navigation and Control Systems Laboratory (iNCSL), School of Intelligent Mechatronics Engineering, and the Department of Convergence Engineering for Intelligent Drone, Sejong University, Seoul 05006, Republic Of Korea ([email protected])r;
(5) Jin Woo Song, Intelligent Navigation and Control Systems Laboratory (iNCSL), School of Intelligent Mechatronics Engineering, and the Department of Convergence Engineering for Intelligent Drone, Sejong University, Seoul 05006, Republic Of Korea ([email protected]).
:::
:::info
This paper is available on arxiv under ATTRIBUTION-NONCOMMERCIAL-NODERIVS 4.0 INTERNATIONAL license.
:::












