Table of Links
Abstract and 1. Introduction
2. Mathematical Description and 2.1. Numerical Algorithms for Nonlinear Equations
2.2. Globalization Strategies
2.3. Sensitivity Analysis
2.4. Matrix Coloring & Sparse Automatic Differentiation
3. Special Capabilities
3.1. Composable Building Blocks
3.2. Smart PolyAlgortihm Defaults
3.3. Non-Allocating Static Algorithms inside GPU Kernels
3.4. Automatic Sparsity Exploitation
3.5. Generalized Jacobian-Free Nonlinear Solvers using Krylov Methods
4. Results and 4.1. Robustness on 23 Test Problems
4.2. Initializing the Doyle-Fuller-Newman (DFN) Battery Model
4.3. Large Ill-Conditioned Nonlinear Brusselator System
5. Conclusion and References
3.2. Smart PolyAlgortihm Defaults
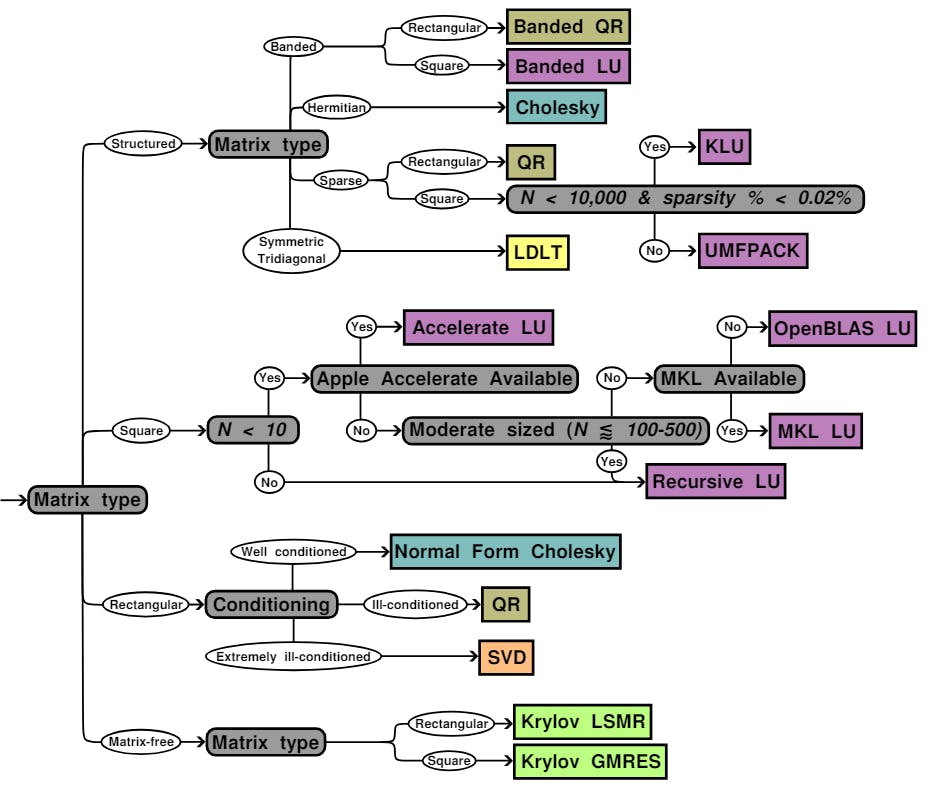
NonlinearSolve.jl comes with a set of well-benchmarked defaults designed to be fast and robust in the average case. For Nonlinear Problems with Intervals, we default to Interpolate, Truncate, and Project (ITP) [48]. For more advanced problems, we default to a polyalgorithm that selects the internal solvers based on the problem specification. Our selection happens twofold, first at the nonlinear solver level [Figure 4] and next at the linear solver level[10] [Figure 5].
3.2.1. Default Nonlinear Solver Selection. By default, we use a polyalgorithm that balances speed and robustness. We start with Quasi-Newton Algorithms – Broyden [49] and Klement [50]. If these fail, we use a modified version of Broyden,
using a true Jacobian initialization. Finally, if Quasi-Newton Methods fail, we use . Newton Raphson with Line Search and finally fall back to Trust Region Methods. Additionally, if a custom Jacobian function is provided or the system is small (≤ 25 states), we avoid using Quasi-Newton Methods and directly use the first-order solvers. We have designed our default to be robust, allowing it to solve all 23 test problems [Subsection 4.1]. Additionally, as seen in Figure 9, our default solver successfully solves new problems. Our default strongly contrasts with other software like Sundials and MINPACK, which can only solve 15 (22 with line search) and 17 (possibly 18, depending on settings) problems, respectively, out of the 23 problems.
3.2.2. Default Linear Solver Selection. For ill-conditioned Jacobians in the linear system (𝐴𝑥 = 𝑏), we default to QR for regular cases or SVD for extremely ill-conditioned cases. We run a polyalgorithm for well-conditioned systems to determine the best linear solver. If 𝐴 is a matrix-free object, we use GMRES [51] from Krylov.jl [52] and solve the linear system without ever materializing the Jacobian.
For other cases, if 𝐴 is reasonably small, we use the native Julia Implementation . of LU Factorization [53] from RecursiveFactorization.jl [54]. We use the LU factorization routines from OpenBLAS or MKL for larger systems if present on the user’s system.
[10] Default Linear Solver selection happens in LinearSolve.jl.
Authors:
(1) AVIK PAL, CSAIL MIT, Cambridge, MA;
(2) FLEMMING HOLTORF;
(3) AXEL LARSSON;
(4) TORKEL LOMAN;
(5) UTKARSH;
(6) FRANK SCHÄFER;
(7) QINGYU QU;
(8) ALAN EDELMAN;
(9) CHRIS RACKAUCKAS, CSAIL MIT, Cambridge, MA.