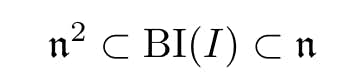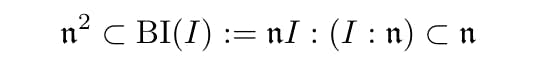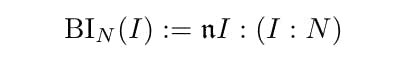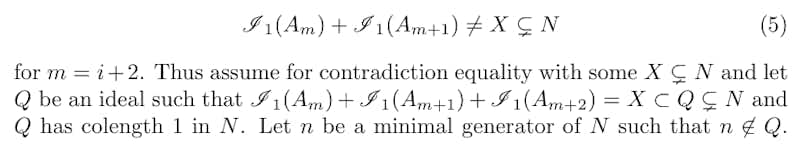Table of Links
1 N-Burch Ideals
2 Burch Duality and Burch Closure
3 Proof of Generalized Burch Index Theorem
4 Untwisting
5 Future Work and References
Consider a minimal free resolution of a module M over a local Noetherian ring R. Over such rings, resolutions are often infinite, for example by the The Auslander-Buchsbaum formula when depth(R) = 0 [1]. The question of periodicity in infinite resolutions is the subject of intensive research for example in the works of Eisenbud, Peeva, and Gasharov, and the central survey of Avramov [6, 5, 7].
We will consider iterated Burch Indices
1 N-Burch Ideals
In this section we will flesh out some of the details of the introduction, and prove some initial results. Throughout this paper, we let (S, n, k) be a regular local ring, and for an ideal I ⊂ S write R = S/I as a local ring (R, m, k). The main thrust of the paper of Eisenbud and Dao is to consider ideals of the form
BI(I) = In : (I : n)
called the Burch Ideal [3]. Eisenbud and Dao restrict to the case where depth(S/I) = 0 and I 6= 0 so that
This allows us to define the Burch index as
We begin weakening the restriction on the original Burch Ideal definitioin. However, we still restrict to the case where I 6= 0 for non-triviality, and remark that periodicity of 1×1 minors is well understood in the regular local ring case. We initially care about cases where depth(S/I) = 0. The reason is twofold. First, from the Auslander-Buchsbaum formula, if the projective dimension of M is finite, then
pd(M) + dim R = depth(M)
Thus if the projectve dimension of M is finite, M is free. Second, this condition, along with I 6= 0, ensures that (I : n) is a proper ideal of R, as it is well known a local Noetherian ring R is depth 0 iff xm = 0 for some nonzero x ∈ R. In particular this allows us to form the bounds
However, we will also consider positive depth rings R in this paper, in which case BI(I) = R since (I : n) = I. When definitions and theorems differ for positive depth rings, we will make a disclaimer.
Let I, N ⊂ S be ideals. We introduce
ote that unlike in the normal Burch ideal case, BIN (I) is not necessarily contained in N, even in the case of depth 0. This is because (I : N) ⊃ (I : J) for all J ⊃ N, and this containment need not be strict. Thus let J ′ = ∪J for all J with (I : N) = (I : J). We have that
Remark 1. If Burch(I) 6= 0, then depth(R) = 0.
2 Burch Duality and Burch Closure
3 Proof of Generalized Burch Index Theorem
We are now equipped to prove the result on generalized Burch Index. First we need a helper lemma.
This allows us to prove the following major lemma. After reading through the lemma, consider again this remark:
4 Untwisting
In other words, under certain conditions, we can check whether the module M has N-periodicity by considering column-wise Burch periodicity of the ideals Q, which have unmixed columns as the minimal generators of Q.
Proof of Lemma 5. We follow a similar proof as Lemma 4. We first show
5 Future Work
References
[1] Maurice Auslander and David A Buchsbaum. “Homological dimension in local rings”. In: Transactions of the American Mathematical Society 85.2 (1957), pp. 390–405.
[2] Michael K Brown, Hailong Dao, and Prashanth Sridhar. “Periodicity of ideals of minors in free resolutions”. In: arXiv preprint arXiv:2306.00903 (2023).
[3] Hailong Dao and David Eisenbud. “Linearity of free resolutions of monomial ideals”. In: Research in the Mathematical Sciences 9.2 (2022), p. 35.
[4] Hailong Dao, Toshinori Kobayashi, and Ryo Takahashi. “Burch ideals and Burch rings”. In: Algebra & Number Theory 14.8 (2020), pp. 2121–2150.
[5] David Eisenbud. “Homological algebra on a complete intersection, with an application to group representations”. In: Transactions of the American Mathematical Society 260.1 (1980), pp. 35–64.
[6] Juan Elias et al. Six lectures on commutative algebra. Vol. 166. Springer Science & Business Media, 1998.
[7] Vesselin N Gasharov and Irena V Peeva. “Boundedness versus periodicity over commutative local rings”. In: Transactions of the American Mathematical Society 320.2 (1990), pp. 569–580.
[8] Daniel R. Grayson and Michael E. Stillman. Macaulay2, a software system for research in algebraic geometry. Available at http://www2.macaulay2.com.
This paper is