Pitting Heuristics Against Exact Solvers in the Flexible Job Shop Gauntlet | HackerNoon

Abstract and 1. Introduction

2. Mixed integer and constraint programming models

   2.1 Mixed-integer linear programming model

   2.2 Constraint Programming model

3. Constructive Heuristics

4. Benchmark instances

5. Numerical experiments

   5.1 Experiments with the constructive heuristics

   5.2 Solving the proposed models with a commercial solver

6. Conclusions and References

4 Benchmark instances

Tractability of the introduced models and performance of the proposed constructive heuristics will be evaluated with the 50 large-sized instances proposed in [4], that were introduced for the FJS scheduling problem with sequence flexibility but without learning effect. In addition to these large-sized instances, a new set with 60 smaller instances, using the generator described in [4], was generated. Instances whose name starts with “Y” correspond to instances in which DAGs that represent the operations’ precedences are Y-shaped (like the DAG in the top of

Figure 1); while instances whose name starts with “DA” correspond to instances in which DAGs that represent the operations precedences are arbitrary DAGs (like the DAG in the bottom of Figure 1). The former will be called instances of Y-type and the latter will be called instances of DA-type from now on.

is also between 0 and 1 and represent the degree of the instance sequencing flexibility. The larger ω1, the larger the search space and, therefore, the more difficult the instance. (Of course, any other type of average could be used in the definition of ω1.)

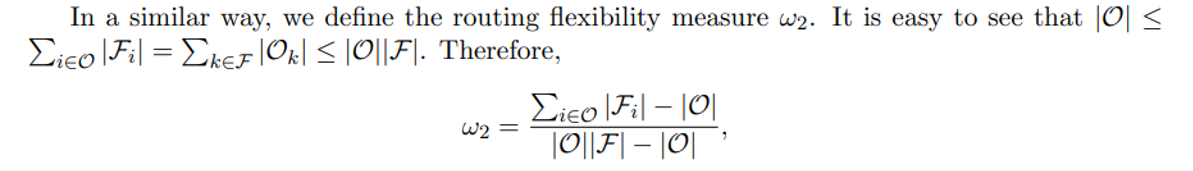
is between 0 and 1. The closer to 1, the larger the search space and, therefore, the harder the instance.

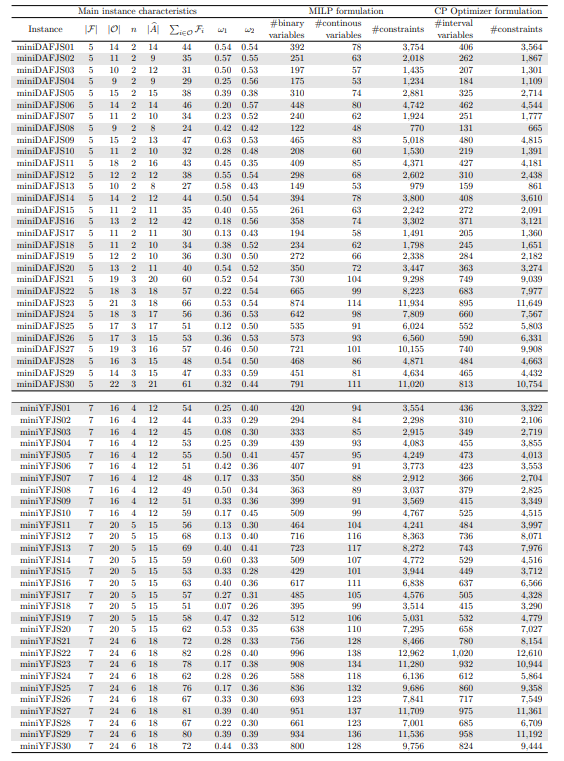
In the small-sized instances of Table 1, the number of binary variables of the MILP models and the number of interval variables of the CP models go up to almost 1,000; while in both models the number of constraints goes up to 13,000. On the other hand, in the large-sized instances of Table 2, the number of binary variables of the MILP models and the number of interval variables of the CP models go up to almost 73,000; while in both models the number of constraints goes up to 4,000,000. Moreover, for each instance, the number of binary variables in its MILP model is very similar to the number of interval variables in its CP model and the two models also have a very similar number of constraints.

5 Numerical experiments

In this section we present numerical experiments. First, we wish to evaluate the two introduced constructive heuristics. Second, we wish to assess the correctness of the MILP and CP models and attempt to infer which of the two, or rather which of the exact commercial solvers applied to each of them, is more effective in finding proven optimal solutions. Third, we wish to determine the usefulness of providing a feasible solution to the exact solvers. It should be noted that all efforts are to build a set of test instances with proven optimal solutions. The models and constructive heuristics presented in this paper are intended to contribute in that respect and are not intended to construct a solution method per se, for a known difficult problem. In all cases we considered the 110 instances introduced in Section 4 with the learning rate α ∈ {0.1, 0.2, 0.3} for a total of 330 instances.

The experiments were carried out in an Intel i9-12900K (12th Gen) processor operating at 5.200GHz and 128 GB of RAM. The constructive heuristics were implemented in C++ programming language. Models were solved using IBM ILOG CPLEX Optimization Studio version 22.1, using default parameters, with concert library and C++. The code was compiled using g++

10.2.1. Benchmark instances and code are available at https://github.com/kennedy94/FJS.

5.1 Experiments with the constructive heuristics

In this subsection, we evaluate the two constructive heuristics. Tables 3 and 4 show the results. For each instance, the lowest makespan, among the solutions found by the two constructive heuristics, is shown in bold. In all instances, the constructive heuristics take less than 0.001 seconds of CPU time to build a solution. Considering the small-sized instances in Table 3, depending on the instance, there may be a significant difference between the solutions found by one and the other constructive heuristic. However, on average, the two heuristics behave basically indistinguishably. For the large-sized instances in Table 4 the comparison is a bit different: there is a clear advantage of the EST constructive heuristic in the DA-type instances, while on the other hand there is a clear advantage of the ECT constructive heuristic in the Y-type instances. It is worth noting that in the small-sized instances there is no clear differentiation between the sequencing flexibility sparsity measure ω1 of the DA-type and the Y-type instances (see Table 1). On the other hand, in the large-sized instances, Y-type instances have a value of ω1 clearly lower than the value of ω1 of DA-type instances. Summarizing, as mentioned at the end of Section 3, the greedy strategy of ECT of choosing the operation/machine pair that terminates first seems to compensate in situations where, because there is already little sequencing flexibility, the greedy choice does not cause a large decrease of the search space.

:::info
Authors:

(1) K. A. G. Araujo, Department of Applied Mathematics, Institute of Mathematics and Statistics, University of Sao Paulo, Rua do Matao, 1010, Cidade Universitaria, 05508-090, Sao Paulo, SP, Brazil ([email protected]);

(2) E. G. Birgin, Department of Computer Science, Institute of Mathematics and Statistics, University of Sao Paulo, Rua do Matao, 1010, Cidade Universitaria, 05508-090, Sao Paulo, SP, Brazil ([email protected]);

(3) D. P. Ronconi, Department of Production Engineering, Polytechnic School, University of Sao Paulo, Av. Prof. Luciano Gualberto, 1380, Cidade Universitaria, 05508-010 Sao Paulo, SP, Brazil ([email protected]).

:::

:::info
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.

:::