Table of Links
1 Introduction
2 Dancing Links
3 The Rust Programming Language
4 RAC: Hardware/Software Co-Assurance at Scale
5 Rust and RAR
5.1 Restricted Algorithmic Rust
6 Dancing Links in Rust and 6.1 Definitions
6.2 Translation to ACL2
6.3 Dancing Links Theorems
7 Related Work
8 Conclusion
9 Acknowledgments and References
“Dancing Links” connotes an optimization to a circular doubly-linked list data structure implementation which provides for fast list element removal and restoration. The Dancing Links optimization is used primarily in fast algorithms to find exact covers, and has been popularized by Knuth in Volume 4B of his seminal series The Art of Computer Programming. We describe an implementation of the Dancing Links optimization in the Rust programming language, as well as its formal verification using the ACL2 theorem prover. Rust has garnered significant endorsement in the past few years as a modern, memory-safe successor to C/C++ at companies such as Amazon, Google, and Microsoft, and is being integrated into both the Linux and Windows operating system kernels. Our interest in Rust stems from its potential as a hardware/software co-assurance language, with application to critical systems. We have crafted a Rust subset, inspired by Russinoff’s Restricted Algorithmic C (RAC), which we have imaginatively named Restricted Algorithmic Rust, or RAR. In previous work, we described our initial implementation of a RAR toolchain, wherein we simply transpile the RAR source into RAC. By so doing, we leverage a number of existing hardware/software co-assurance tools with a minimum investment of time and effort. In this paper, we describe the RAR Rust subset, describe our improved prototype RAR toolchain, and detail the design and verification of a circular doubly-linked list data structure employing the Dancing Links optimization in RAR, with full proofs of functional correctness accomplished using the ACL2 theorem prover.
1 Introduction
The exact cover problem [17], in its simplest form, attempts to find, for an n × m matrix with binary elements, all of the subsets of the rows of the matrix such that all the column sums are exactly one. This basic notion naturally extends to matrix elements that are in some numerical range; indeed, the popular puzzle game Sudoku is an extended exact cover problem for a 9× 9 matrix with element values in the range of 1 to 9, inclusive.
The exact cover problem is NP-complete, but computer scientists have devised recursive, nondeterministic backtracking algorithms to find exact covers. One such procedure is Knuth’s Algorithm X, described in [17]. In this algorithm, elements of the matrix are connected via circular doubly-linked lists, and individual elements are removed, or restored, as the algorithm proceeds, undergoing backtracking, etc. As these removals and restorations out of/into the list are quite common, making these operations efficient is a laudable goal. This is where Knuth’s “Dancing Links” comes in, resulting in an optimized algorithm for finding exact covers which Knuth calls DLX (Dancing Links applied to algorithm X).
2 Dancing Links
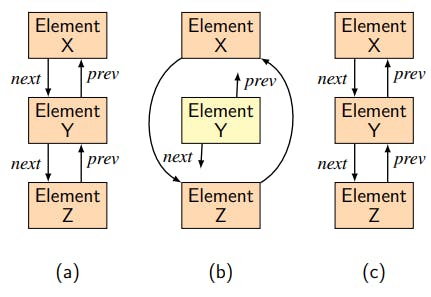
The concept behind Dancing Links is quite simple: when a given element Y of a list is removed in an exact cover algorithm, it is very likely that this same element will later be restored. Thus, rather
than “zero out” the ‘previous’ and ‘next’ links associated with element Y, as good programming hygiene would normally dictate, in Dancing Links, the programmer leaves the link values in place for the removed element. The Dancing Links remove operator thus deletes element Y from the list, setting the ’next’ element of the preceding element X to the following element Z, and setting the ’previous’ element of Z to a link to X, but not touching the ’next’ and ’previous’ links of the removed element Y. on, if Y needs to be restored, it is simply hooked back in to the list using a simple restore operator. In Knuth’s words, if one monitors the list links as the DLX algorithm proceeds, the links appear to ‘dance’, hence the name. Knuth’s Dancing Links functionality is summarized in Fig. 1.