Table of Links
Abstract and 1. Introduction
1.1 A Polyethylene-based metamaterial for acoustic control
2 Relaxed micromorphic modelling of finite-size metamaterials
2.1 Tetragonal Symmetry / Shape of elastic tensors (in Voigt notation)
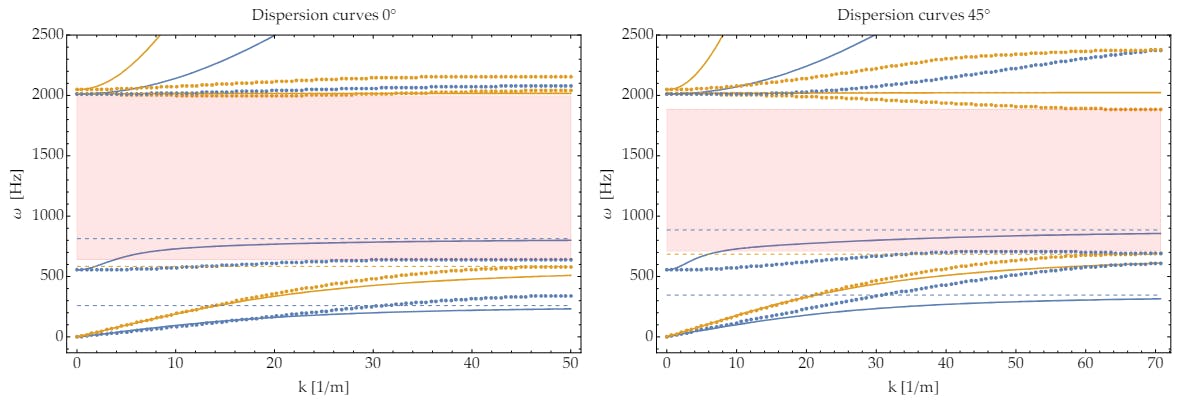
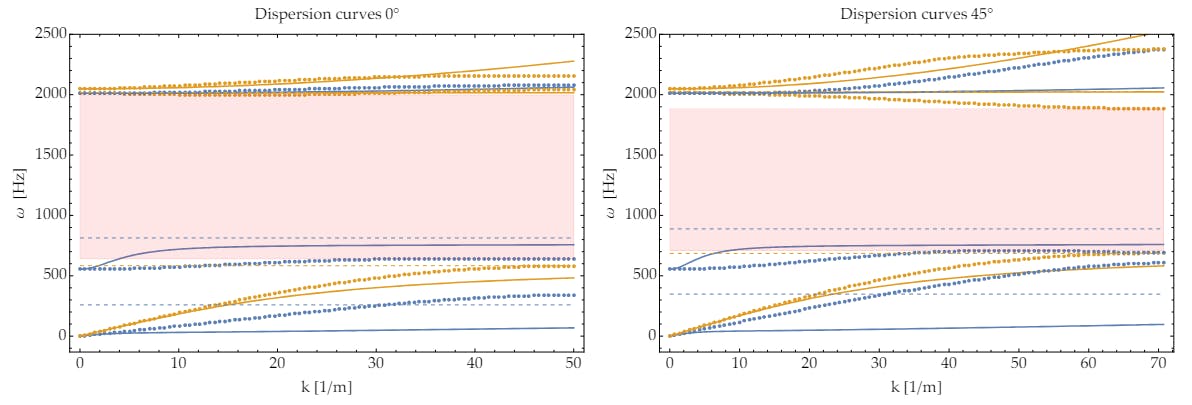
3 Dispersion curves
4 New considerations on the relaxed micromorphic parameters
4.1 Consistency of the relaxed micromorphic model with respect to a change in the unit cell’s bulk material properties
4.2 Consistency of the relaxed micromorphic model with respect to a change in the unit cell’s size
4.3 Relaxed micromorphic cut-offs
5 Fitting of the relaxed micromorphic parameters: the particular case of vanishing curvature (without Curl P and Curl P˙)
5.1 Asymptotes
5.2 Fitting
5.3 Discussion
6 Fitting of the relaxed micromorphic parameters with curvature (with Curl P)
6.1 Asymptotes and 6.2 Fitting
6.3 Discussion
7 Fitting of the relaxed micromorphic parameters with enhanced kinetic energy (with Curl P˙) and 7.1 Asymptotes
7.2 Fitting
7.3 Discussion
8 Summary of the obtained results
9 Conclusion and perspectives, Acknowledgements, and References
A Most general 4th order tensor belonging to the tetragonal symmetry class
B Coefficients for the dispersion curves without Curl P
C Coefficients for the dispersion curves with P
D Coefficients for the dispersion curves with P◦
7.1 Asymptotes
Again, the cut-offs are independent on the coefficients with higher order of k and thus they do not change with respect to the two previous cases. For the asymptotes we only consider the terms with the highest order of k available and compute
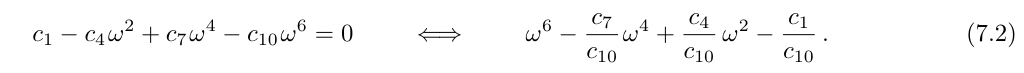
We have again three asymptotes (the roots of a third order polynomial) which in general causes the analytical expressions to be impractical rather quickly. However, in this case it is possible to find one root by hand

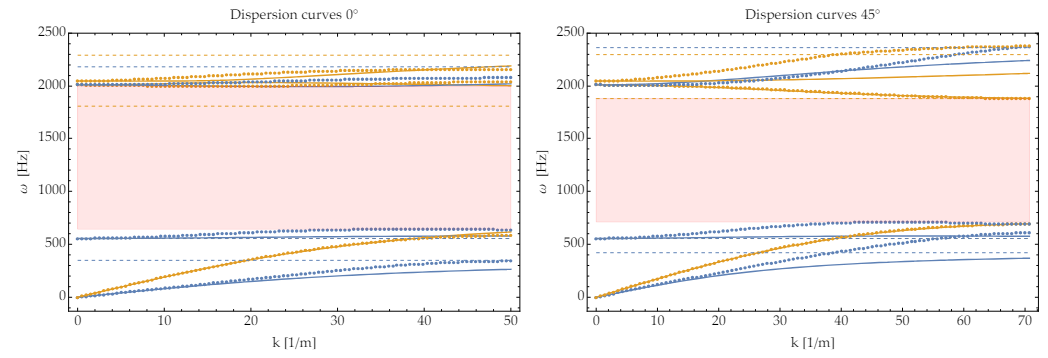
7.2 Fitting

7.3 Discussion

:::info
This paper is available on arxiv under CC BY 4.0 DEED license.
:::
:::info
Authors:
(1) Jendrik Voss, Institute for Structural Mechanics and Dynamics, Technical University Dortmund and a Corresponding Author ([email protected]);
(2) Gianluca Rizzi, Institute for Structural Mechanics and Dynamics, Technical University Dortmund;
(3) Patrizio Neff, Chair for Nonlinear Analysis and Modeling, Faculty of Mathematics, University of Duisburg-Essen;
(4) Angela Madeo, Institute for Structural Mechanics and Dynamics, Technical University Dortmund.
:::