Tracking Reward Function Improvement with Proxy Human Preferences in ICPL | HackerNoon

Table of Links

1. Abstract and Introduction
2. Related Work
3. Problem Definition
4. Method
5. Experiments
6. Conclusion and References

A. Appendix

A.1. Full Prompts and A.2 ICPL Details

A. 3 Baseline Details

A.4 Environment Details

A.5 Proxy Human Preference

A.6 Human-in-the-Loop Preference

A.5 PROXY HUMAN PREFERENCE

A.5.1 ADDITIONAL RESULTS

Due to the high variance in LLMs performance, we report the standard deviation across 5 experiments as a supplement, which is presented in Table 5 and Table 6. We also report the final task score of PrefPPO using sparse rewards as the preference metric for the simulated teacher in Table 7.

A.5.2 IMPROVEMENT ANALYSIS

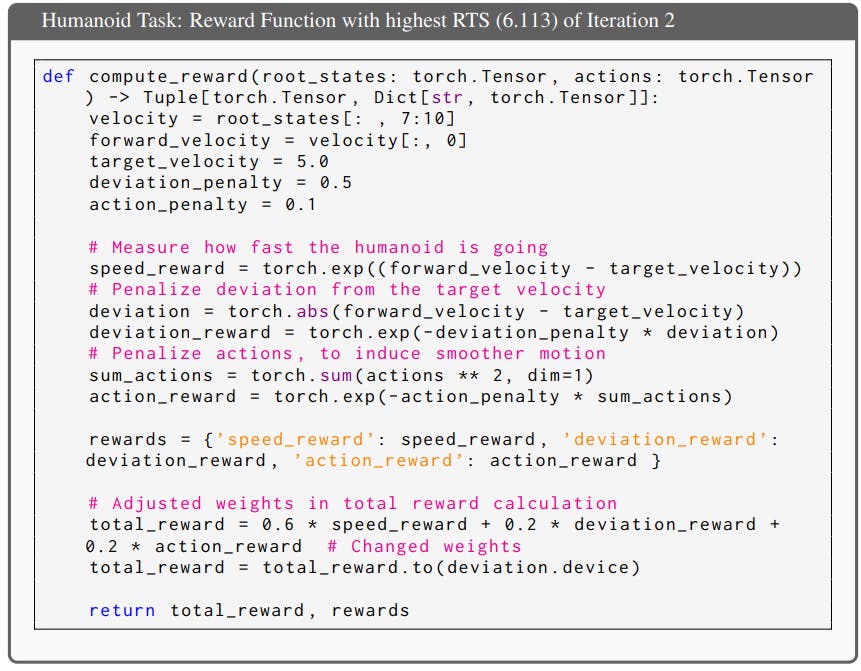
We use a trial of the Humanoid task to illustrate how ICPL progressively generated improved reward functions over successive iterations. The task description is “to make the humanoid run as fast as possible”. Throughout five iterations, adjustments were made to the penalty terms and reward weightings. In the first iteration, the total reward was calculated as 0.5 × speed_reward + 0.25 × deviation_reward+0.25×action_reward, yielding an RTS of 5.803. The speed reward and deviation reward motivate the humanoid to run fast, while the action reward promotes smoother motion. In the second iteration, the weight of the speed reward was increased to 0.6, while the weights for deviation and action rewards were adjusted to 0.2 each, improving the RTS to 6.113. In the third iteration, the action penalty was raised and the reward weights were further modified to 0.7 × speed_reward, 0.15×deviation_reward, and 0.15×action_reward, resulting in an RTS of 7.915. During the fourth iteration, the deviation penalty was reduced to 0.35 and the action penalty was lowered, with the reward weights set to 0.8, 0.1, and 0.1 for speed, deviation, and action rewards, respectively. This change led to an RTS of 8.125. Finally, in the fifth iteration, an additional upright reward term was incorporated, with the total reward calculated as 0.7 × speed_reward + 0.1 × deviation_reward + 0.1 × action_reward + 0.1 × upright_reward. This adjustment produced the highest RTS of 8.232. Below are the specific reward functions produced at each iteration during one experiment.