Table of Links
Abstract, Acknowledgements, and Statements and Declarations
-
Introduction
-
Background and Related Work
2.1 Agent-based Financial Market simulation
2.2 Flash Crash Episodes
-
Model Structure and 3.1 Model Set-up
3.2 Common Trader Behaviours
3.3 Fundamental Trader (FT)
3.4 Momentum Trader (MT)
3.5 Noise Trader (NT)
3.6 Market Maker (MM)
3.7 Simulation Dynamics
-
Model Calibration and Validation and 4.1 Calibration Target: Data and Stylised Facts for Realistic Simulation
4.2 Calibration Workflow and Results
4.3 Model Validation
-
2010 Flash Crash Scenarios and 5.1 Simulating Historical Flash Crash
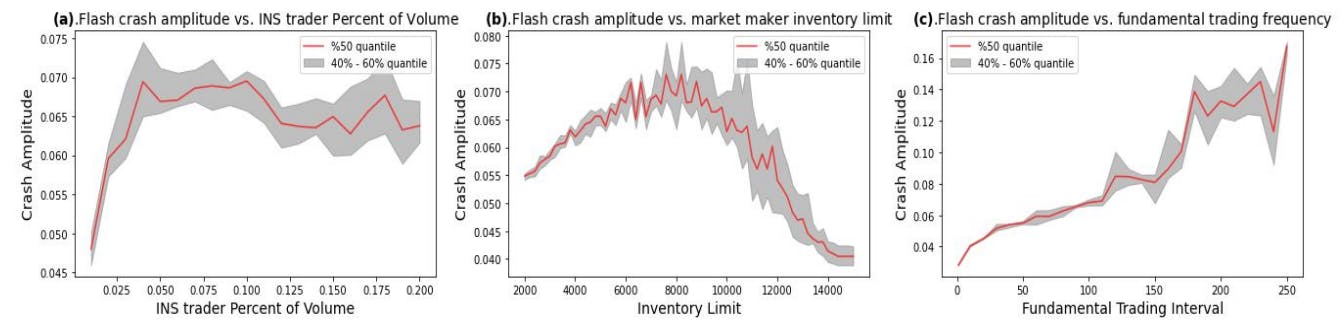
5.2 Flash Crash Under Different Conditions
-
Mini Flash Crash Scenarios and 6.1 Introduction of Spiking Trader (ST)
6.2 Mini Flash Crash Analysis
6.3 Conditions for Mini Flash Crash Scenarios
-
Conclusion and Future Work
7.1 Summary of Achievements
7.2 Future Works
References and Appendices
4.2 Calibration Workflow and Results
The focus of this paper is not on specific methods for calibration; instead, we will pay more attention to the validation part. Here we briefly present the calibration process. The calibration workflow has two stages in our experiments. The main calibration technique in the first stage is the surrogate modelling approach, proposed by Lamperti et al. (2018). Specifically, an XGBoost surrogate model is built to approximate the agent-based model simulation. The surrogate model is capable of intelligently guiding the exploration of the parameter space. Estimated parameter values are those that give rise to smaller stylised facts distance, indicating that simulated moments match those observed empirically.
After the first stage of the calibration, optimal parameters are given by the surrogate model. Even though global optimum is not guaranteed, it is shown in our experiments that the obtained parameter combination yields small stylised facts distance and is capable of reproducing realistic price dynamics. It is likely that the global optimal parameters are located close to the parameters generated by the first stage. Taking this into consideration, a numerical grid search over a feasible bounded set of parameters is carried out. The feasible set of parameters is centered around the optimal parameters given by the surrogate modelling approach in stage one. The parameter combination that yields the smallest stylised facts distance is selected as the final calibrated model parameter combination. Calibrated model parameter values for each trading day, as well as the yielded stylised facts distance, are presented in Table 2.
Figure 3 compares empirical time series of mid-price on May 5th to simulated mid-price time series. Visual inspection shows that the model produces price time series whose dynamics are very similar to those in empirical data. Nevertheless, quantitative assessment is required to validate the proposed simulation model, which is presented in the subsequent section.
Authors:
(1) Kang Gao, Department of Computing, Imperial College London, London SW7 2AZ, UK and Simudyne Limited, London EC3V 9DS, UK ([email protected]);
(2) Perukrishnen Vytelingum, Simudyne Limited, London EC3V 9DS, UK;
(3) Stephen Weston, Department of Computing, Imperial College London, London SW7 2AZ, UK;
(4) Wayne Luk, Department of Computing, Imperial College London, London SW7 2AZ, UK;
(5) Ce Guo, Department of Computing, Imperial College London, London SW7 2AZ, UK.
[8] Due to the flash crash event in the afternoon trading session on May 6th, 2010, only the first half of the trading data (8:00-12:30) is used to calibrate the model parameters for this trading day.