Table of Links
-
Introduction
-
Hypothesis testing
2.1 Introduction
2.2 Bayesian statistics
2.3 Test martingales
2.4 p-values
2.5 Optional Stopping and Peeking
2.6 Combining p-values and Optional Continuation
2.7 A/B testing
-
Safe Tests
3.1 Introduction
3.2 Classical t-test
3.3 Safe t-test
3.4 χ2 -test
3.5 Safe Proportion Test
-
Safe Testing Simulations
4.1 Introduction and 4.2 Python Implementation
4.3 Comparing the t-test with the Safe t-test
4.4 Comparing the χ2 -test with the safe proportion test
-
Mixture sequential probability ratio test
5.1 Sequential Testing
5.2 Mixture SPRT
5.3 mSPRT and the safe t-test
-
Online Controlled Experiments
6.1 Safe t-test on OCE datasets
-
Vinted A/B tests and 7.1 Safe t-test for Vinted A/B tests
7.2 Safe proportion test for sample ratio mismatch
-
Conclusion and References
8 Conclusion
The myriad issues with p-values and their interpretation have led statisticians to seek new methods of information discovery. Classical statistical tests are unable to suit common research practices, such as early stopping or optional continuation of experiments. This disparity is becoming more noticeable with modern technological processes that allow frequent statistical analysis of data. Statistical objects such as test martingales and Bayes factors are seeing increased adoption as safer, more intuitive methods of hypothesis testing. In this thesis, we have explored safe testing as a solution to meet the needs of practitioners. In particular, we have focused on detecting small effect sizes common to A/B testing at large-scale technology companies.
The safe t-test was introduced as an anytime-valid substitute for the classical t-test. It was shown that the safe t-test uses, on average, less data to reject a null hypothesis. The effectiveness of the safe t-test was demonstrated for a wide range of effect sizes, significance levels, and statistical powers. On real world data, there remain discrepancies between the effects detected by the safe t-test and the classical t-test. Novelty effects can lead to an increased number of false positives, while batch processing increases the number of false negatives. There are also considerations in the delay between test exposure time and realization. This leads us to suggest that the ideal scenario for safe t-tests in large scale experimentation platforms is in granular data that is readily available. An A/B test’s target metric is often a slow metric designed to improve the overall performance of the platform of its users. Secondary and guardrail metrics can be measured and analyzed much more quickly. These metrics are ideal candidates for safe tests to continuously monitor the performance of an A/B test.
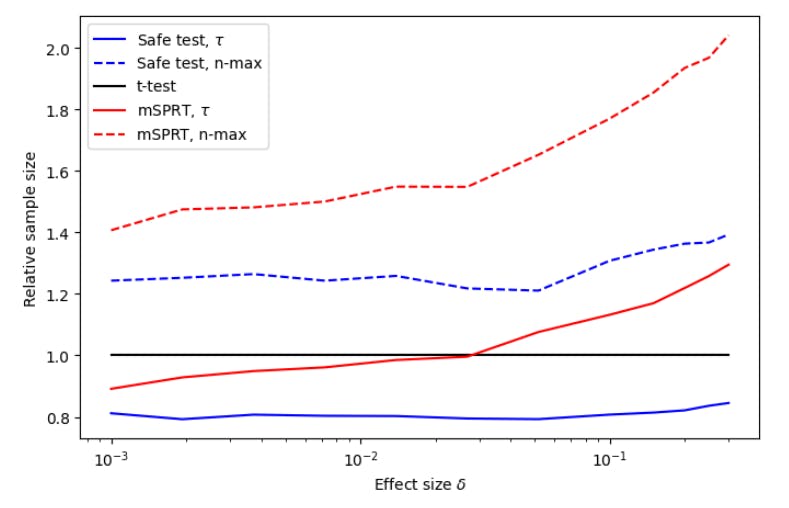
The performance of the safe t-test was rigorously compared to the mSPRT. Through extensive simulation and benchmarking on real datasets, it was found that the safe t-test outperforms the mSPRT in all situations. This should encourage practitioners to adopt the safe t-test as their preferred anytime-valid test.
The safe proportion test was also validated as an anytime-valid test for contingency tables. Through simulation it was found that the safe proportion test requires less data to reach a decision than the χ2 test, on average. The tests agree considerably on real-world data to detect sample ratio mismatch. With the benefit of taking full advantage of modern data infrastructure, adoption of the safe proportion test to detect SRM will proceed at Vinted.
Despite the effectiveness of safe testing, it will likely take time and persistence on behalf of its proponents before it reaches wide-scale adoption. The greatest challenge will be in educating practitioners familiar with classical statistics. The concepts introduced in this thesis require a higher level of statistical knowledge than is common to most scientists and A/B test experimenters. If a practitioner using a safe test gets a different result than the classical alternative, there is not an intuitive way to explain this difference. Conversely, it may be easier for practitioners to understand E-variables conceptually. Due to their intrinsic interpretation as evidence against the null hypothesis, E-variables seem easier to grasp than p-values. Given the widespread misinterpretation of p-values, E-variables may give experimenters a better understanding of their results.
While there are challenges, we remain optimistic about the future applications of safe testing. It meets the needs of experimenters who need flexible testing scenarios based on observed evidence. In addition, research into E-variables is continuing to develop, which will lead to more safe tests and better education. With packages available in both R and Python, it has become easier for practitioners to introduce safe testing in their experiments. For this reason, we believe that safe testing will proliferate as an anytime-valid testing methodology.
References
[AGM19] Valentin Amrhein, Sander Greenland, and Blake McShane. “Scientists rise up against statistical significance”. en. In: Nature 567.7748 (Mar. 2019), pp. 305– 307.
[Aze+20] Eduardo M. Azevedo, Alex Deng, José Luis Montiel Olea, Justin Rao, and E. Glen Weyl. “A/B Testing with Fat Tails”. In: Journal of Political Economy 128.12 (Dec. 2020). doi: 10.1086/710607.
[Den+13] Alex Deng, Ya Xu, Ron Kohavi, and Toby Walker. “Improving the sensitivity of online controlled experiments by utilizing pre-experiment data”. In: Proceedings of the sixth ACM international conference on Web search and data mining. 2013, pp. 123–132.
[GHK23] Peter Grünwald, Rianne de Heide, and Wouter Koolen. Safe Testing. 2023. arXiv: 1906.07801 [math.ST].
[GLW18] Quentin F. Gronau, Alexander Ly, and Eric-Jan Wagenmakers. Informed Bayesian T-Tests Online Appendix. 2018. arXiv: 1704.02479 [stat.ME]. url: https: //www.tandfonline.com/doi/suppl/10.1080/00031305.2018.1562983? scroll=top&role=tab.
[Hea+15] Megan L Head, Luke Holman, Rob Lanfear, Andrew T Kahn, and Michael D Jennions. “The extent and consequences of p-hacking in science”. en. In: PLoS Biol. 13.3 (Mar. 2015), e1002106. [HR18] N A Heard and P Rubin-Delanchy. “Choosing between methods of combining pvalues”. In: Biometrika 105.1 (Jan. 2018), pp. 239–246. doi: 10.1093/biomet/ asx076. url: https://doi.org/10.1093%2Fbiomet%2Fasx076.
[Joh+17] Ramesh Johari, Pete Koomen, Leonid Pekelis, and David Walsh. “Peeking at A/B Tests: Why it matters, and what to do about it”. In: Aug. 2017, pp. 1517– 1525. isbn: 978-1-4503-4887-4. doi: 10.1145/3097983.3097992.
[Liu+22] C. H. Bryan Liu, Ângelo Cardoso, Paul Couturier, and Emma J. McCoy. Datasets for Online Controlled Experiments. 2022. arXiv: 2111.10198 [stat.AP].
[LR05] E. L. Lehmann and Joseph P. Romano. Testing statistical hypotheses. Third. Springer Texts in Statistics. New York: Springer, 2005, pp. xiv+784. isbn: 0-387-98864-5.
[LTT20] Alexander Ly, Robert Turner, and Joris Ter Schure. R-package safestats. https: //github.com/AlexanderLyNL/safestats. 2020.
[Pér+22] Muriel Felipe Pérez-Ortiz, Tyron Lardy, Rianne de Heide, and Peter Grünwald. E-Statistics, Group Invariance and Anytime Valid Testing. 2022. arXiv: 2208. 07610 [math.ST].
[SA23] Mårten Schultzberg and Sebastian Ankargren. Choosing Sequential Testing Framework — Comparisons and Discussions. Accessed: 2023-07-04. Feb. 2023. url: https://engineering.atspotify.com/2023/03/choosing-sequentialtesting-framework-comparisons-and-discussions.
[Sha+11] Glenn Shafer, Alexander Shen, Nikolai Vereshchagin, and Vladimir Vovk. “Test Martingales, Bayes Factors and p-Values”. In: Statistical Science 26.1 (Feb. 2011). doi: 10.1214/10- sts347. url: https://doi.org/10.1214%2F10- sts347.
[TLG22] Rosanne Turner, Alexander Ly, and Peter Grünwald. Generic E-Variables for Exact Sequential k-Sample Tests that allow for Optional Stopping. 2022. arXiv: 2106.02693 [stat.ME].
[Tur19] Rosanne J Turner. “Safe tests for 2 x 2 contingency tables and the CochranMantel-Haenszel test”. In: (2019).
[Vil39] J. Ville. Étude critique de la notion de collectif, par Jean Ville … GauthierVillars, 1939. url: https://books.google.lt/books?id=ztJKswEACAAJ.
[Wal45] A. Wald. “Sequential Tests of Statistical Hypotheses”. In: The Annals of Mathematical Statistics 16.2 (1945), pp. 117–186. issn: 00034851. url: http:// www.jstor.org/stable/2235829 (visited on 07/04/2023).
[WL16] Ronald L. Wasserstein and Nicole A. Lazar. “The ASA Statement on p-Values: Context, Process, and Purpose”. In: The American Statistician 70.2 (2016), pp. 129–133. doi: 10.1080/00031305.2016.1154108. eprint: https://doi. org/10.1080/00031305.2016.1154108. url: https://doi.org/10.1080/ 00031305.2016.1154108.
[WW48] A. Wald and J. Wolfowitz. “Optimum Character of the Sequential Probability Ratio Test”. In: The Annals of Mathematical Statistics 19.3 (1948), pp. 326– 339. doi: 10.1214/aoms/1177730197. url: https://doi.org/10.1214/ aoms/1177730197.
[Xu+22] Ziyu Xu, Luke Sonnet, Umashanthi Pavalanathan, and Brent Cohn. “Evaluating the effectiveness of safe, anytime-valid inference (SAVI) for sample ratio mismatch detection at Twitter”. In: (2022).
Author:
(1) Daniel Beasley
This paper is