Why Your Auction Mechanism Might Be Vulnerable to Collusion | HackerNoon

Table of Links

Abstract and 1. Introduction

1.1 Our Contributions

1.2 TFM Incentive-Compatibility Notions: A Cheat Sheet

2. Definitions

   2.1 Transaction Fee Mechanism

   2.2 Incentive Compatibility Notions

3. Preliminary: Myerson’s Lemma

4. Warmup: Impossibility of UIC + MIC + Global SCP for Deterministic Mechanisms

5. Impossibility of UIC + MIC + Global SCP for Randomized Mechanisms and 5.1 Proof Roadmap

   5.2 Formal Proofs

6. Feasibility and Impossibility of UIC + MIC + OCA-Proof

   6.1 A Non-Truthful Mechanism with UIC + MIC + OCA-Proof

   6.2 Impossibility of UIC + MIC + OCA-Proof for Truthful Mechanisms

7. How to Circumvent the Impossibilities and 7.1 Allowing the Globally Optimal Strategy to Coordinate

   7.2 Allowing the Globally Optimal Strategy to Output Multiple Bids

   7.3 Inclusion-Rule-Respecting and 7.4 Discussions and Open Questions Regarding the Use of Cryptography

8. Static Revelation Principle for Transaction Fee Mechanisms

   8.1 Static Revelation Principle: Bidding Rules That Output Single Bid

   8.2 Static Revelation Principle: Allowing Bidding Rules that Output Multiple Bids

A. Comparison of Collusion-Resilience Notions

References

A Comparison of Collusion-Resilience Notions

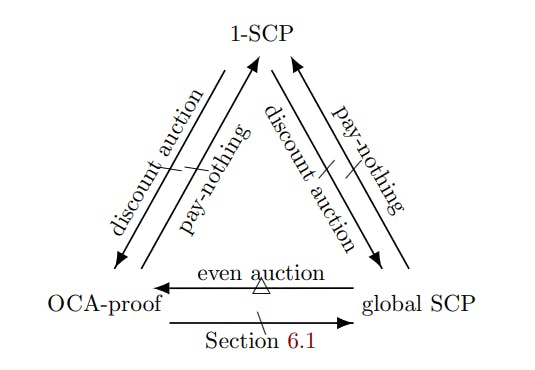
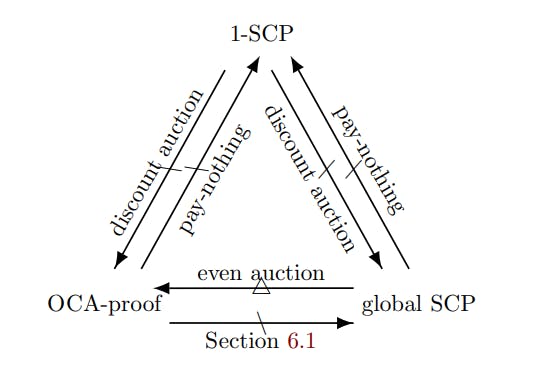
Lemma A.1. The even auction above satisfies global SCP but not OCA-proofness.

Notice that whether the individually rational bidding strategy σ outputs a single bid or multiple bids is important. If we require σ to only output a single real as we defined in Definition 6, there is no non-trivial TFM that can satisfy UIC, MIC, and OCA-proofness as we proved in Theorem 6.9. However, if we allow σ to output multiple bids, we obtain a feasibility in Section 7.2.

When we analyze whether a TFM satisfies c-SCP for some c, 1-SCP is the weakest requirement since c′ -SCP always implies c-SCP for any c′ > c by definition. Interestingly, even so, 1-SCP is incomparable with global SCP and OCA-proofness. The relations between 1-SCP, global SCP, and OCA-proofness is depicted in Figure 1.

We explain Figure 1 in more detail below:

Below, we introduce the (somewhat contrived) auctions for constructing the counterexamples.

Lemma A.2. The pay-nothing auction above satisfies global SCP and OCA-proofness. However, it does not satisfy 1-SCP.

Lemma A.3. The discount auction above satisfies 1-SCP. However, it does not satisfy global SCP or OCA-proofness.

Now, we show that the mechanism does not satisfy OCA-proofness. Imagine a scenario where there are 10 users each with the true value r. Without injecting any fake bid, the lowest possible payment for each user is f(10) = r, so the social welfare is at most 0. However, if the global coalition inject one fake bid r, everyone’s payment will further lower to f(11) = r/2. In this case, the social welfare becomes 10r − 11r/2 = 9r/2 > 0. Thus, the mechanism does not satisfy OCA-proofness.

The mechanism does not satisfy global SCP either since the bidding rule only outputs a single real. If the mechanism satisfied global SCP, the global coalition could pick the suggested bidding rule as the individually rational bidding strategy σ to maximize the social welfare. Given that the mechanism does not satisfy OCA-proofness, it cannot satisfy global SCP either.

References

[ACH11] Gilad Asharov, Ran Canetti, and Carmit Hazay. Towards a game theoretic view of secure computation. In Eurocrypt, 2011.

[ADGH06] Ittai Abraham, Danny Dolev, Rica Gonen, and Joseph Halpern. Distributed computing meets game theory: Robust mechanisms for rational secret sharing and multiparty computation. In PODC, 2006.

[AL11] Gilad Asharov and Yehuda Lindell. Utility dependence in correct and fair rational secret sharing. Journal of Cryptology, 24(1), 2011.

[BCD+] Vitalik Buterin, Eric Conner, Rick Dudley, Matthew Slipper, and Ian Norden. Ethereum improvement proposal 1559: Fee market change for eth 1.0 chain. https://github.com/ethereum/EIPs/blob/master/EIPS/eip-1559.md.

[BEOS19] Soumya Basu, David A. Easley, Maureen O’Hara, and Emin G¨un Sirer. Towards a functional fee market for cryptocurrencies. CoRR, abs/1901.06830, 2019.

[BGR23] Maryam Bahrani, Pranav Garimidi, and Tim Roughgarden. Transaction fee mechanism design with active block producers. arXiv preprint arXiv:2307.01686, 2023.

[CCWS21] Kai-Min Chung, T-H. Hubert Chan, Ting Wen, and Elaine Shi. Game-theoretic fairness meets multi-party protocols: The case of leader election. In CRYPTO. Springer-Verlag, 2021.

[CGL+18] Kai-Min Chung, Yue Guo, Wei-Kai Lin, Rafael Pass, and Elaine Shi. Game theoretic notions of fairness in multi-party coin toss. In TCC, volume 11239, pages 563–596, 2018.

[CMW23] Davide Crapis, Ciamac C Moallemi, and Shouqiao Wang. Optimal dynamic fees for blockchain resources. arXiv preprint arXiv:2309.12735, 2023.

[CS23] Hao Chung and Elaine Shi. Foundations of transaction fee mechanism design. In Proceedings of the 2023 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), pages 3856–3899. SIAM, 2023.

[DR07] Yevgeniy Dodis and Tal Rabin. Cryptography and game theory. In AGT, 2007.

[EFW22] Meryem Essaidi, Matheus V. X. Ferreira, and S. Matthew Weinberg. Credible, strategyproof, optimal, and bounded expected-round single-item auctions for all distributions. In Mark Braverman, editor, 13th Innovations in Theoretical Computer Science Conference, ITCS 2022, January 31 – February 3, 2022, Berkeley, CA, USA, volume 215 of LIPIcs, pages 66:1–66:19, 2022.

[FMPS21] Matheus V. X. Ferreira, Daniel J. Moroz, David C. Parkes, and Mitchell Stern. Dynamic posted-price mechanisms for the blockchain transaction-fee market. CoRR, abs/2103.14144, 2021.

[FW20] Matheus V. X. Ferreira and S. Matthew Weinberg. Credible, truthful, and two-round (optimal) auctions via cryptographic commitments. In Peter Biro, Jason D. Hartline, Michael Ostrovsky, and Ariel D. Procaccia, editors, EC ’20: The 21st ACM Conference on Economics and Computation, Virtual Event, Hungary, July 13-17, 2020, pages 683– 712. ACM, 2020.

[GKM+13] Juan A. Garay, Jonathan Katz, Ueli Maurer, Björn Tackmann, and Vassilis Zikas. Rational protocol design: Cryptography against incentive-driven adversaries. In FOCS, 2013.

[GKTZ15] Juan Garay, Jonathan Katz, Björn Tackmann, and Vassilis Zikas. How fair is your protocol? a utility-based approach to protocol optimality. In PODC, 2015.

[GLR10] Ronen Gradwohl, Noam Livne, and Alon Rosen. Sequential rationality in cryptographic protocols. In FOCS, 2010.

[GTZ15] Juan A. Garay, Björn Tackmann, and Vassilis Zikas. Fair distributed computation of reactive functions. In DISC, volume 9363, pages 497–512, 2015.

[GY22] Yotam Gafni and Aviv Yaish. Greedy transaction fee mechanisms for (non-) myopic miners. arXiv preprint arXiv:2210.07793, 2022.

[GY24] Yotam Gafni and Aviv Yaish. Barriers to collusion-resistant transaction fee mechanisms. arXiv preprint arXiv:2402.08564, 2024.

[HT04] Joseph Halpern and Vanessa Teague. Rational secret sharing and multiparty computation. In STOC, 2004.

[Kat08] Jonathan Katz. Bridging game theory and cryptography: Recent results and future directions. In Theory of Cryptography Conference, pages 251–272. Springer, 2008.

[KKLP23] Aggelos Kiayias, Elias Koutsoupias, Philip Lazos, and Giorgos Panagiotakos. Tiered mechanisms for blockchain transaction fees. arXiv preprint arXiv:2304.06014, 2023.

[KMSW22] Ilan Komargodski, Shin’ichiro Matsuo, Elaine Shi, and Ke Wu. log*-round gametheoretically-fair leader election. In CRYPTO, 2022.

[KN08] Gillat Kol and Moni Naor. Cryptography and game theory: Designing protocols for exchanging information. In TCC, 2008.

[LRMP23] Stefanos Leonardos, Daniel Reijsbergen, Barnabe Monnot, and Georgios Piliouras. Optimality despite chaos in fee markets. In International Conference on Financial Cryptography and Data Security, pages 346–362. Springer, 2023.

[LSZ19] Ron Lavi, Or Sattath, and Aviv Zohar. Redesigning bitcoin’s fee market. In The World Wide Web Conference, WWW 2019, pages 2950–2956, 2019. [Mye81] Roger B. Myerson. Optimal auction design. Math. Oper. Res., 6(1), 1981.

[Ndi23] Abdoulaye Ndiaye. Blockchain price vs. quantity controls. Quantity Controls (July 27, 2023), 2023.

[OPRV09] Shien Jin Ong, David C. Parkes, Alon Rosen, and Salil P. Vadhan. Fairness with an honest minority and a rational majority. In TCC, 2009.

[PS17] Rafael Pass and Elaine Shi. Fruitchains: A fair blockchain. In PODC, 2017.

[Rou20] Tim Roughgarden. Transaction fee mechanism design for the Ethereum blockchain: An economic analysis of EIP-1559. Manuscript, https://timroughgarden.org/papers/eip1559.pdf, 2020.

[Rou21] Tim Roughgarden. Transaction fee mechanism design. In EC, 2021.

[SCW23] Elaine Shi, Hao Chung, and Ke Wu. What can cryptography do for decentralized mechanism design? In ITCS, volume 251 of LIPIcs, pages 97:1–97:22. Schloss Dagstuhl – Leibniz-Zentrum fur Informatik, 2023.

[TY23] Wenpin Tang and David D Yao. Transaction fee mechanism for proof-of-stake protocol. arXiv preprint arXiv:2308.13881, 2023.

[WAS22] Ke Wu, Gilad Asharov, and Elaine Shi. A complete characterization of gametheoretically fair, multi-party coin toss. In Eurocrypt, 2022.

[WSC24] Ke Wu, Elaine Shi, and Hao Chung. Maximizing Miner Revenue in Transaction Fee Mechanism Design. In Venkatesan Guruswami, editor, 15th Innovations in Theoretical Computer Science Conference (ITCS 2024), 2024.

[XFP23] Matheus Venturyne Xavier Ferreira and David C Parkes. Credible decentralized exchange design via verifiable sequencing rules. In Proceedings of the 55th Annual ACM Symposium on Theory of Computing, pages 723–736, 2023.

[Yao] Andrew Chi-Chih Yao. An Incentive Analysis of Some Bitcoin Fee Designs (Invited Talk). In ICALP 2020.

[ZCZ22] Zishuo Zhao, Xi Chen, and Yuan Zhou. Bayesian-nash-incentive-compatible mechanism for blockchain transaction fee allocation. https://arxiv.org/abs/2209.13099, 2022.