Table of Links
-
Introduction
-
Hypothesis testing
2.1 Introduction
2.2 Bayesian statistics
2.3 Test martingales
2.4 p-values
2.5 Optional Stopping and Peeking
2.6 Combining p-values and Optional Continuation
2.7 A/B testing
-
Safe Tests
3.1 Introduction
3.2 Classical t-test
3.3 Safe t-test
3.4 χ2 -test
3.5 Safe Proportion Test
-
Safe Testing Simulations
4.1 Introduction and 4.2 Python Implementation
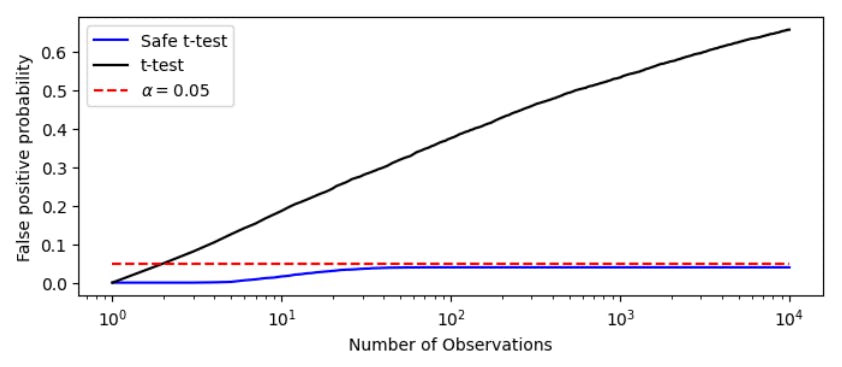
4.3 Comparing the t-test with the Safe t-test
4.4 Comparing the χ2 -test with the safe proportion test
-
Mixture sequential probability ratio test
5.1 Sequential Testing
5.2 Mixture SPRT
5.3 mSPRT and the safe t-test
-
Online Controlled Experiments
6.1 Safe t-test on OCE datasets
-
Vinted A/B tests and 7.1 Safe t-test for Vinted A/B tests
7.2 Safe proportion test for sample ratio mismatch
-
Conclusion and References
2 Hypothesis testing
2.1 Introduction
Hypothesis testing is science’s method of assigning truth. Beginning with a null hypothesis stating the current belief, the objective of a test is to determine whether or not to reject the null hypothesis [LR05]. The decision is based on the realization of a random variable X with distribution Pθ, where Pθ belongs to a class {Pθ : θ ∈ Θ}. This hypothesis class is divided into regions which accept or reject the hypothesis. For a null hypothesis H0, we let Θ0 represent the subset of Θ for which H0 is true, and Θ1 be the subset for which H0 is false. This is equivalent to writing θ ∈ Θ0 and θ ∈ Θ1, respectively. There may be an alternative hypothesis H1 = {Pθ : θ ∈ Θ1} to the null hypothesis H0. In the Bayesian formulation of hypothesis testing there is always an alternative H1, though it is not required in all frequentist formulations. If Θ1 = {θ1}, a single point, then H1 is called simple. Conversely, if |Θ1| > 1, then H1 is composite. The notation H0 : θ = θ0 is a condensed way of writing H0 = {Pθ : θ = θ0}.
The result of a test comes from the decision function δ(X) which can take value d0 to accept H0 or value d1 to reject H0. Since the problem of hypothesis testing is stochastic, there always exists the possibility of committing one of two errors. The first type of error occurs when the null hypothesis is rejected when it is true, i.e. δ(X) = d1 for some θ ∈ Θ0. This is known as a Type I error or false positive. A statistical test bounds the Type I error probability by the significance level α which represents the maximum probability that this error has occurred. Mathematically, this is written as
The second type of error occurs when the hypothesis is not rejected when it is false: δ(X) = d0 when θ ∈ Θ1. This error is known as a Type II error, or false negative result. For any classical statistical test, this will also have a nonzero probability β:
The quantity 1 − β is known as the power of the test. This is the probability that the test correctly rejects the hypothesis in the case that it is false. For a given α, we aim to maximize the power, which depends on the sample size of the experiment.
The sample size of an experiment is the number of samples that must be collected in order to make a decision. In the process of designing a classical experiment, the experimenter will usually determine the sample size in advance. This requires assessing three quantities: the significance level α, the power 1 − β, and the unknown effect size δ. The effect size is the difference between the two groups of subjects, often a combination of their mean difference and their variances. The effect size may be estimated when it is an unknown quantity, or fixed to a minimum relevant effect size, for example in clinical studies. A decrease in any of the three quantities α, β, or δ will lead to larger sample sizes for experiments, and similarly increases lead to smaller samples sizes.
Historically, much of statistical testing has centered on frequentist statistics, however Bayesian statistics offers invaluable techniques for learning from data. Next, we take a deeper look at the concepts of Bayesian statistics.
2.2 Bayesian statistics
The ratio of marginal distributions with respect to the alternative hypothesis H1 and the null hypothesis H0 is known as the Bayes factor :
The Bayes factor can be thought of as the amount of evidence in favour of the alternative against the null. As we will later see, Bayes factors are intricately linked with safe testing. Another important concept in this theory is that of test martingales.
2.3 Test martingales
We will now continue of our discussion of hypothesis testing with the infamous p-value.
Author:
(1) Daniel Beasley
This paper is