Table of Links
Abstract and 1. Introduction
1.1. Introductory remarks
1.2. Basics of neural networks
1.3. About the entropy of direct PINN methods
1.4. Organization of the paper
-
Non-diffusive neural network solver for one dimensional scalar HCLs
2.1. One shock wave
2.2. Arbitrary number of shock waves
2.3. Shock wave generation
2.4. Shock wave interaction
2.5. Non-diffusive neural network solver for one dimensional systems of CLs
2.6. Efficient initial wave decomposition
-
Gradient descent algorithm and efficient implementation
3.1. Classical gradient descent algorithm for HCLs
3.2. Gradient descent and domain decomposition methods
-
Numerics
4.1. Practical implementations
4.2. Basic tests and convergence for 1 and 2 shock wave problems
4.3. Shock wave generation
4.4. Shock-Shock interaction
4.5. Entropy solution
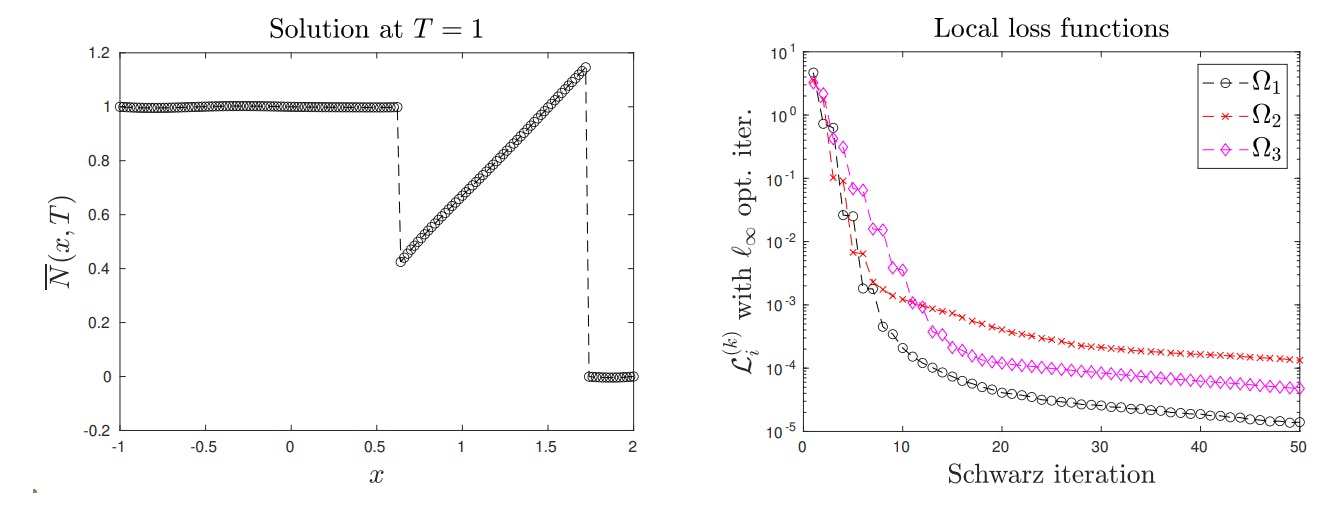
4.6. Domain decomposition
4.7. Nonlinear systems
-
Conclusion and References
5. Conclusion
In this paper, we have proposed an original method for solving hyperbolic conservation laws using a non-diffusive neural network method. The principle of the method is to track
the DLs and solve the conservation laws in the subdomains the DLs define, and where the solution is smooth. We have used neural networks to approximate the DLs and the solution of conservation laws in each of the subdomains. The networks are trained by minimizing a loss functional that measures the (norm of the) residues of conservation laws, boundary and initial conditions and Rankine-Hugoniot conditions. This approach allows for a computation of shock waves without using a weak formulation of HCL. Other functions could be used to approximate the solution and the DLs, but neural networks provide interesting features. Indeed, they allow for automatic differentiation, which avoids the approximation errors for the derivatives, facilitates the implementation of the algorithm, and allows for an accurate/diffusion-free computation of shock waves, solutions to nonlinear hyperbolic conservation laws.
When the global loss functional approach is slow to converge, a rapidly convergent and embarrassingly parallel (Schwarz) domain decomposition method can be used. The latter allows for a decoupling of the optimization procedure thanks to the optimization of local neural networks approximating from which the global approximate solution is reconstructed, as shown in [23].
In a future work, we plan to apply to this methodology to higher dimensional problems.
CRediT authorship contribution statement
The authors have contributed equally.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Data availability
No data was used for the research described in this article.
References
[1] J.-M. Ghidaglia and F. Pascal. The normal flux method at the boundary for multidimensional finite volume approximations in CFD. Eur. J. Mech. B Fluids, 24(1):1–17, 2005.
[2] E. Godlewski and P.-A. Raviart. Hyperbolic systems of conservation laws, volume 3/4 of Math´ematiques & Applications (Paris) [Mathematics and Applications]. Ellipses, Paris, 1991.
[3] D. Serre. Syst`emes de lois de conservation. I. Fondations. [Foundations]. Diderot Editeur, Paris, 1996. Hyperbolicit´e, entropies, ondes de choc. [Hyperbolicity, entropies, shock waves].
[4] P. G. LeFloch. Hyperbolic systems of conservation laws. Lectures in Mathematics ETH Z¨urich. Birkh¨auser Verlag, Basel, 2002. The theory of classical and nonclassical shock waves.
[5] J. Smoller. Shock waves and reaction-diffusion equations, volume 258 of Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Science]. Springer-Verlag, New York-Berlin, 1983.
[6] E. Godlewski and P.-A. Raviart. Numerical approximation of hyperbolic systems of conservation laws, volume 118 of Applied Mathematical Sciences. Springer-Verlag, New York, 1996.
[7] B. Despr´es. Lax theorem and finite volume schemes. Math. Comput., 74(247).
[8] M. Laforest and P. G. LeFloch. Diminishing functionals for nonclassical entropy solutions selected by kinetic relations. Port. Math., 67(3), 2010.
[9] I.E. Lagaris, A. Likas, and D.I. Fotiadis. Artificial neural networks for solving ordinary and partial differential equations. IEEE Transactions on Neural Networks, 9(5):987– 1000, 1998.
[10] M. Raissi, P. Perdikaris, and G.E. Karniadakis. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378:686–707, 2019.
[11] G. Pang, L. Lu, and G.E. Karniadakis. fPINNs: fractional physics-informed neural networks. SIAM J. Sci. Comput., 41(4):A2603–A2626, 2019.
[12] L. Yang, D. Zhang, and G. E. Karniadakis. Physics-informed generative adversarial networks for stochastic differential equations. SIAM J. Sci. Comput., 42(1):A292–A317, 2020.
[13] J. Han, A. Jentzen, and Weinan E. Solving high-dimensional partial differential equations using deep learning. Proc. Natl. Acad. Sci. USA, 115(34):8505–8510, 2018.
[14] H. Gao, M. J. Zahr, and J.-X. Wang. Physics-informed graph neural Galerkin networks: a unified framework for solving PDE-governed forward and inverse problems. Comput. Methods Appl. Mech. Engrg., 390:Paper No. 114502, 18, 2022.
[15] J. Sirignano and K. Spiliopoulos. DGM: a deep learning algorithm for solving partial differential equations. J. Comput. Phys., 375:1339–1364, 2018.
[16] A.D. Jagtap, E. Kharazmi, and G.E. Karniadakis. Conservative physics-informed neural networks on discrete domains for conservation laws: Applications to forward and inverse problems. Computer Methods in Applied Mechanics and Engineering, 365, 2020.
[17] R. Rodriguez-Torrado, P. Ruiz, and L. Cueto-Felgueroso. Physics-informed attentionbased neural network for hyperbolic partial differential equations: application to the Buckley–Leverett problem. Sci Rep., 12:7557, 2022.
[18] R. G. Patel, I. Manickam, N. A. Trask, M. A. Wood, M. Lee, I. Tomas, and E. C. Cyr. Thermodynamically consistent physics-informed neural networks for hyperbolic systems. J. of Comput. Phys., 449:110754, 2022.
[19] E. Lorin and X. Yang. Schwarz waveform relaxation-learning for advection-diffusionreaction equations. J. Comput. Phys., 473:Paper No. 111657, 2023.
[20] E. Lorin and X. Yang. Neural network-based quasi-optimal domain decomposition method for computing the Schr¨odinger equation. Comput. Phys. Commun., Accepted. 2024. [21] M. Gander and L. Halpern. Optimized Schwarz waveform relaxation methods for advection reaction diffusion problems. SIAM J. on Numer. Anal., 45(2):666–697, 2007.
[22] M.J. Gander, F. Kwok, and B.C. Mandal. Dirichlet–Neumann waveform relaxation methods for parabolic and hyperbolic problems in multiple subdomains. BIT Numerical Mathematics, 61(1):173–207, 2021.
[23] M.J. Gander and C. Rohde. Overlapping Schwarz waveform relaxation for convectiondominated nonlinear conservation laws. SIAM Journal on Scientific Computing, 27(2):415–439, 2006.
[24] X. Antoine and E. Lorin. An analysis of Schwarz waveform relaxation domain decomposition methods for the imaginary-time linear Schrodinger and Gross-Pitaevskii equations. Numerische Mathematik, 137(4):923–958, 2017.
[25] L. Bottou, F. E. Curtis, and J. Nocedal. Optimization methods for large-scale machine learning. SIAM Rev., 60(2):223–311, 2018.
[26] Bradbury J, R. Frostig, P. Hawkins, M. J. Johnson, C. Leary, D. Maclaurin, G. Necula, A. Paszke, J. VanderPlas, S. Wanderman-Milne, and Q. Zhang. JAX: composable transformations of Python+NumPy programs, 2018. [
27] J.L. Montagne, H.C. Yee, and M. Vinokur. Comparative study of high-resolution shockcapturing schemes for a real gas. in: Proc. seventh gamm conf. on numerical methods in fluid mechanics, (Lauvain-la-Neuve, Belgium: sep. 9-11, 1987), m. Devill, 20 (ISBN 3-528-08094-9), 1987.
[28] P. L. Roe. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys., 43(2):357–372, 1981.
[29] L. Halpern and J. Szeftel. Optimized and quasi-optimal Schwarz waveform relaxation for the one-dimensional Schr¨odinger equation. Mathematical Models and Methods in Applied Sciences, 20(12):2167–2199, 2010.
[30] X. Antoine, F. Hou, and E. Lorin. Asymptotic estimates of the convergence of classical Schwarz waveform relaxation domain decomposition methods for two-dimensional stationary quantum waves. ESAIM: Numerical Analysis and Mathematical Modeling (M2AN), 52(4):1569–1596, 2018.
[31] X. Antoine and E. Lorin. On the rate of convergence of Schwarz waveform relaxation methods for the time-dependent Schr¨odinger equation. J. Comput. Appl. Math., 354:15– 30, 2019.
[32] X. Antoine, C. Besse, and P. Klein. Absorbing boundary conditions for the onedimensional Schr¨odinger equation with an exterior repulsive potential. J. Comput. Phys., 228(2):312–335, 2009.
[33] A. Modave, A. Royer, X. Antoine, and C. Geuzaine. A non-overlapping domain decomposition method with high-order transmission conditions and cross-point treatment for Helmholtz problems. Comput. Methods Appl. Mech. Engrg., 368:113162, 23, 2020.
[34] I. Badia, B. Caudron, X. Antoine, and C. Geuzaine. A well-conditioned weak coupling of boundary element and high-order finite element methods for time-harmonic electromagnetic scattering by inhomogeneous objects. SIAM J. Sci. Comput., 44(3):B640–B667, 2022.
[35] X. Antoine and C. Besse. Unconditionally stable discretization schemes of non-reflecting boundary conditions for the one-dimensional Schrodinger equation. J. Comput. Phys., 188(1):157–175, 2003.
[36] R. Gorenflo. Fractional calculus: Some numerical methods. In CISM Courses and Lectures, volume 378. Springer, 1997.
[37] X. Antoine, E. Lorin, and Q. Tang. A friendly review to absorbing boundary conditions and perfectly matched layers for classical and relativistic quantum wave equations. Molecular Physics, to appear, 115, 2017.
[38] N.J. Ford and J.A. Connolly. Comparison of numerical methods for fractional differential equations. Communications on Pure and Applied Analysis, 5(2):289–307, 2006.
[39] X. Antoine and H. Barucq. Microlocal diagonalization of strictly hyperbolic pseudodifferential systems and application to the design of radiation conditions in electromagnetism. SIAM J. Appl. Math., 61(6):1877–1905 (electronic), 2001.
[40] G. Carleo, I. Cirac, K. Cranmer, L. Daudet, M. Schuld, N. Tishby, L. Vogt-Maranto, and L. Zdeborov´a. Machine learning and the physical sciences. Rev. Mod. Phys., 91:045002, Dec 2019.
[41] G. Carleo and M. Troyer. Solving the quantum many-body problem with artificial neural networks. Science, 355(6325):602–606, 2017.
[42] X. Antoine, C. Besse, and P. Klein. Absorbing boundary conditions for the twodimensional Schr¨odinger equation with an exterior potential. Part I: Construction and a priori estimates. Math. Models Methods Appl. Sci., 22(10):1250026, 38, 2012.
[43] X. Antoine and C. Besse. Construction, structure and asymptotic approximations of a microdifferential transparent boundary condition for the linear Schr¨odinger equation. J. Math. Pures Appl. (9), 80(7):701–738, 2001.
[44] L. Nirenberg. Lectures on linear partial differential equations. American Mathematical Society, Providence, R.I., 1973.
:::info
Authors:
(1) Emmanuel LORIN, School of Mathematics and Statistics, Carleton University, Ottawa, Canada, K1S 5B6 and Centre de Recherches Mathematiques, Universit´e de Montr´eal, Montreal, Canada, H3T 1J4 ([email protected]);
(2) Arian NOVRUZI, a Corresponding Author from Department of Mathematics and Statistics, University of Ottawa, Ottawa, ON K1N 6N5, Canada ([email protected]).
:::
:::info
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
:::