Abstract and 1. Introduction
-
Mixed integer and constraint programming models
2.1 Mixed-integer linear programming model
2.2 Constraint Programming model
-
Constructive Heuristics
-
Benchmark instances
-
Numerical experiments
5.1 Experiments with the constructive heuristics
5.2 Solving the proposed models with a commercial solver
-
Conclusions and References
2 Mixed integer and constraint programming models
In this section, we present mixed-integer linear programming (MILP) and constraint programming (CP) formulations for the FJS scheduling problem with sequencing flexibility and position-based learning effect.


2.1 Mixed-integer linear programming model
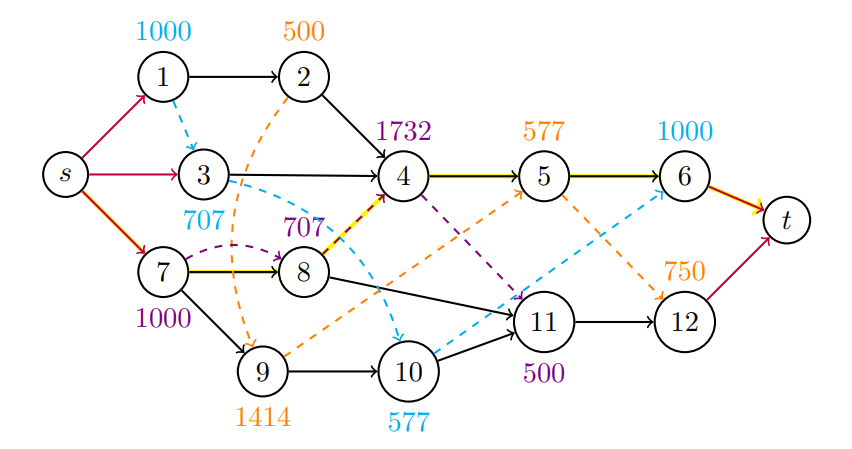
The adoption of position-based decision variables serves as the fundamental approach for modeling problems involving position-based learning effects, as it enables a more natural expression of constraints related to the change in processing times. The proposed MILP model is derived from [4] and is built upon the model introduced in [25] that considers position-based decision variables; see also [26]. Notation below simplifies the presentation of the model.

The MILP model follows.
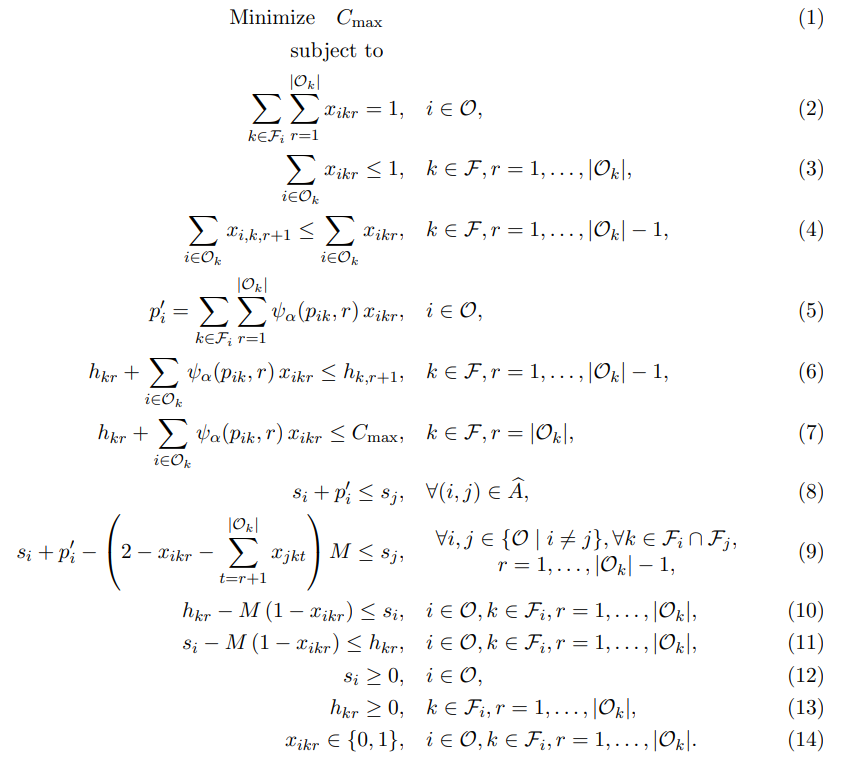

2.2 Constraint Programming model
Constraint Programming (CP) is a potent methodology widely employed for solving scheduling problems in academic and industrial literature. CP Optimizer [19], being an optimization commercial solver rooted in CP, incorporates specialized concepts of constraints and variables, significantly facilitating the modeling process for scheduling problems. In this section, we introduce a CP model specifically designed for its utilization in connection with CP Optimizer. The syntax of CP Optimizer is defined as it arises within the formulation. The model follows below.


3 Constructive Heuristics
In this section, we propose two constructive heuristics for the FJS scheduling problem with sequencing flexibility and position-based learning effect. Constructive heuristics are algorithms that build a feasible solution from scratch by iteratively selecting and sequencing one operation at a time. The two proposed constructive heuristics are based on the earliest starting time (EST) rule [4] and the earliest completion time (ECT) rule [20]. The goal is to use them to provide an initial feasible solution to the exact solver that will be used to attempt to solve a set of test instances.




Algorithm 4 presents the constructive heuristic based on the ECT rule. The algorithm is very similar to Algorithm 1, except for one detail. In the constructive heuristic based on EST, we first compute the instant rmin which is the earliest instant at which an unscheduled operation could be initiated. All operation/machine pairs that could start at that instant are considered and the pair with the shortest processing time is selected. But since they would all start at instant rmin, saying that the pair with the shortest processing time is chosen is the same as saying that the pair that ends earliest is selected. This is the idea that is taken to the extreme in the constructive heuristic based on the ECT rule: without limiting the choice to the operation/machine pairs that could start as early as possible, the operation/machine pair that will finish earliest is chosen, even if the processing of the operation does not start as early as

possible. The worst case time complexity of Algorithm 4 is the same as that of Algorithm 1.
The EST-based heuristic gives priority to those pairs operations/machines that can start the earliest. At the beginning of the construction, this corresponds, roughly, to giving priority to all the first operations of each job, which are operations that have no precedents (operations 1, 3 and 7 in the example of Figure 1). Still, due to the intention of scheduling operations as early as possible, it is possible that preference is given to empty machines, building solutions that use several machines. By rapidly scheduling the first operations of each job, more operations come to have their precedents scheduled, increasing the number of possibilities (search space) in future iterations of the method. On the other hand, the heuristic based on the ECT rule chooses the operation/machine pairs that terminate the earliest, regardless of whether they are the ones that can start the earliest or not. Such a strategy can limit the number of operation/machine pairs available in future iterations, reducing the search space of the method. Moreover, the choice for the operation/machine pair that can finish earliest, combined with the learning effect, leads the method to schedule operations on machines that already have several operations assigned to them, since the higher the position in the machine, the shortest de processing (reduced by the positioned-based learning effect). This leads to the construction of solutions in which not all machines are used. Depending on the learning rate α considered and the density of the DAG of precedences of the instance at hand, one heuristic may be better than the other.
:::info
Authors:
(1) K. A. G. Araujo, Department of Applied Mathematics, Institute of Mathematics and Statistics, University of Sao Paulo, Rua do Matao, 1010, Cidade Universitaria, 05508-090, Sao Paulo, SP, Brazil ([email protected]);
(2) E. G. Birgin, Department of Computer Science, Institute of Mathematics and Statistics, University of Sao Paulo, Rua do Matao, 1010, Cidade Universitaria, 05508-090, Sao Paulo, SP, Brazil ([email protected]);
(3) D. P. Ronconi, Department of Production Engineering, Polytechnic School, University of Sao Paulo, Av. Prof. Luciano Gualberto, 1380, Cidade Universitaria, 05508-010 Sao Paulo, SP, Brazil ([email protected]).
:::
:::info
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
:::










