Don’t Just Train Your AI, Re-Train It: The Weekly Workout Plan for a Smarter Option Hedge | HackerNoon

Table of Links

Abstract and 1. Introduction

2. Deep Reinforcement Learning

3. Similar Work

   3.1 Option Hedging with Deep Reinforcement Learning

   3.2 Hyperparameter Analysis

4. Methodology

   4.1 General DRL Agent Setup

   4.2 Hyperparameter Experiments

   4.3 Optimization of Market Calibrated DRL Agents

5. Results

   5.1 Hyperparameter Analysis

   5.2 Market Calibrated DRL with Weekly Re-Training

6. Conclusions

Appendix

References

4 Methodology

4.1 General DRL Agent Setup

All experiments in this study employ the DDPG algorithm to train DRL agents. Moreover, the rectified linear unit (ReLu) activation function is used as the activation function for both the actor and critic hidden layers. The critic output is linear, and the actor output is transformed by a sigmoid and multiplied by −1 to map the output to the range [0, −1], which aligns with the desired hedging action for a short American put. The DRL state-space is the same as Pickard et al. (2024) and consists of the current asset price, the time-to-maturity, and the current holding (previous action). The rest of the hyperparameters, i.e., the actor and critic learning rates, the actor and critic NN architectures, the number of episodes, and the steps per episode, will vary across the experiments. The reward function will also vary across experiments, with different transaction cost penalties being investigated. These hyperparameter analyses are detailed in the next subsection.

4.2 Hyperparameter Experiments

The first round of analysis in this article is focused on examining hyperparameter impact on DRL American option hedging performance. For all hyperparameter experiments, training data is in the form of simulated paths of the GBM process. The time-to-maturity is one year, the option is at the money with a strike of $100, the volatility is 20%, and the risk-free-rate is equal to the mean expected return of 5%. All tests also use GBM data, and each test consists of 10k episodes, consistent with Pickard et al. (2024). Note that to assess the robustness and consistency of DRL agents, testing will be performed with transaction cost rates of both 1 and 3%. Table 1 summarizes the hyperparameters used in Pickard et al. (2024), and for each experiment, the hyperparameters not being analysed are held fixed at these values. This set of hyperparameters is referred to as the base case.

A first experiment will examine how DRL agent performance is impacted by actor and critic learning rates as a function of episodes. Specifically, a grid search is performed using actor learning rates of 1e-6, 5e-6, and 10e-6, critic learning rates of 1e4, 5e-4, and 10e-4, and episode lengths of 2500, 5000, and 7500. A second experiment will assess the impact of neural-network architectures. Similar to the first experiment, tests will be conducted across actor learning rates of 1e-6, 5e-6, and 10e-6, critic learning rates of 1e-4, 5e-4, and 10e-4, and NN architectures of 322 , 642 , and 643 , for both the actor and critic networks, respectively.

Next, an experiment is conducted to evaluate the impact of training steps. Here, DRL agents are trained using 10, 25, and 50 steps over the year of hedging. Moreover, to examine whether there is a performance impact based on the difference between training steps and testing re-balance periods, testing will be conducted by considering environments with 52 (weekly), 104 (bi-weekly), and 252 (daily) re-balancing times. To be clear, in this study, the steps per episode is synonymous with re-balance periods. As such, for this particular hyperparameter experiment, the training is comprised of 10, 25, and 50 rebalance periods (steps), spaced equally throughout the episode (which has length of 1 year), and the testing is comprised of 52, 104, and 252 rebalance periods (steps).

4.3 Optimization of Market Calibrated DRL Agents

After the hyperparameter analysis, this study looks to improve on the key result from Pickard et al. (2024), wherein it is shown that DRL agents trained with paths from a market calibrated stochastic volatility model outperform DRL agents on the true asset paths between the option sale and maturity dates. One key shortcoming in the findings from Pickard et al. (2024) is that the stochastic volatility model is only calibrated to the option data on the sale date, and the agent trained with model is used to hedge the entire life of the option. As such, if any cases presented themselves where the market changed drastically between the sale and the maturity, this would render the agent obsolete, as it had been trained to hedge in a completely different environment. As such, it is hypothesized that performance will improve by re-training agents to new data at weekly intervals.

Given that the underlying asset data now stems from a stochastic volatility model, an alternative method is required for providing the DRL agent reward with the option price at each training step. While in the GBM experiments, the option price required for the DRL agent reward on each training step is obtained by interpolating a binomial tree, tree methods for stochastic volatility processes increase in complexity due to the requirement of a second spatial dimension. As such, Pickard et al. (2024) detail a Chebyshev interpolation method, first introduced in Glau et al. (2018), to provide the agent with the American option price at each time step in training.

Chebyshev interpolation involves weighting orthogonal interpolating polynomials to approximate a known function within predetermined upper and lower bounds at each time step. Computing an American option price via Chebyshev interpolation involves a three-step process:

1. Discretize the computational space from 𝑡0 = 0 to 𝑡𝑁 = 𝑇. Then, Chebyshev nodes are generated between the upper and lower bounds at 𝑡𝑁−1 and paths are simulated from these nodes to maturity at 𝑡𝑁. The continuation value is computed as the discounted average payoff for all nodes at 𝑡𝑁−1 The value function for Chebyshev nodes at 𝑡𝑁−1 is determined by comparing the continuation value with the immediate exercise payoff

2. For the next time step, 𝑡𝑁−2, the process is repeated by simulating paths from 𝑡𝑁−2 to 𝑡𝑁−1 and performing Chebyshev interpolation between nodes at 𝑡𝑁−1. This continues backward in time until 𝑡 = 𝑡0, and by indexing optimal exercise nodes, a Chebyshev exercise boundary is computed.

3. After completing steps 1 and 2, value functions become accessible at every node throughout the discretized computational space. Consequently, with a specified asset price level and time step, Chebyshev interpolation can be utilized to calculate the price of an option. This step may be called at any time step in the DRL agent training process, without repeating steps 1 and 2.

It is noted first that the Chebyshev approach is agnostic to the underlying asset evolution process, allowing for easy transitions to more complex environments.

A common alternative for computing option prices for a stochastic volatility case is to simulate several thousand MC paths from the current asset price level to maturity or exercise, where the exercise boundary is often computed using the Longstaff-Schwartz Monte Carlo (LSMC) method (Longstaff and Schwartz 2001). However, incorporating a simulation-based pricing method into the training of a reinforcement learning (RL) agent would substantially prolong the training duration, as each training step would necessitate a new set of simulations. For instance, in this study, a base case training loop comprises 5000 episodes, each spanning 25 steps. Consequently, a total of 125,000 sets of simulations would be requiring, an unnecessary addition to an already time-intensive procedure of training a neural network. For a more complete description of the Chebyshev method and its advantages over simulationbased LSMC pricing, the reader is directed to Glau et al. (2018).

As described, this studies employs a strategy wherein each week, a new model is calibrated, new Chebyshev nodes are generated for pricing, and a DRL agent is trained to hedge according to the current market conditions. Note that the stochastic volatility model is the same as in Pickard et al. (2024), which is an adaptation of the SABR model (Hagan et al. 2002):

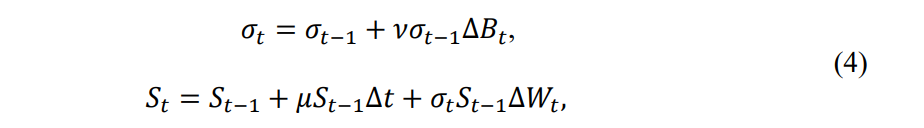
where 𝐵𝑡 and 𝑊𝑡 are Brownian motions with increments given by

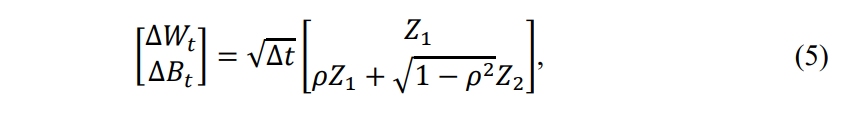
noting that 𝑍1 and 𝑍2 are independent standard normal random variables. In this stochastic volatility model, 𝜌 and 𝜈 are model coefficients that may be used to calibrate the model to empirical observations. Specifically, option data is retrieved for 8 symbols and 5 strikes each. The first training date is October 16th, 2023, and the maturity for all options is November 17th, 2023. In one round of training, DRL agents are trained only using paths from the stochastic volatility model calibrated to data on October 16th. In a second round, DRL agents are trained to hedge only a week at a time. One agent is trained using the data from Monday, October 16th and to hedge only 5 days into the future. A new agent is trained from data available on Monday, October 23rd, and is again trained to hedge for 5 days. The process repeats, with new agents trained using data from October 30th, November 6th, and November 13th, respectively.

A comparison is then given by testing agents on the true asset paths between October 16th and November 17th, using 1 and 3% transaction costs. Note that the BS Delta method is used as a benchmark. Specifically, the BS delta uses the volatility from the weekly re-calibrated stochastic volatility model. Table 2 summarizes the option data. The base case hyperparameters are used for this analysis.

Table 2: Option Data Summary

| Symbol | Strikes |
|—-|—-|
| GE | $100, $105, $110, $115, $120 |
| XOM | $100, $105, $110, $115, $120 |
| DELL | $60, $65, $70, $75, $80 |
| PEP | $150, $155, $160, $165, $170 |
| AMZN | $125, $130, $135, $140, $145 |
| TSLA | $210 $215, $220, $225, $230 |
| TXN | $135, $140, $145, $150, $155 |
| AIG | $50, $55, $60, $65, $70 |

:::info
Authors:

(1) Reilly Pickard, Department of Mechanical and Industrial Engineering, University of Toronto, Toronto, Canada ([email protected]);

(2) F. Wredenhagen, Ernst & Young LLP, Toronto, ON, M5H 0B3, Canada;

(3) Y. Lawryshyn, Department of Chemical Engineering, University of Toronto, Toronto, Canada.

:::

:::info
This paper is available on arxiv under CC BY-NC-ND 4.0 Deed (Attribution-Noncommercial-Noderivs 4.0 International) license.

:::