Table of Links
I. Introduction
II. Theoretical Aspects
III. Experimental Setup
IV. Results and Discussion
V. Conclusion and References
III. EXPERIMENTAL SETUP
The laser (TOPTICA-TopMode 405) with a center wavelength of 405 nm and bandwidth of 0.01 pm emits a Gaussian beam. The beam passes through a half-wave plate (HWP) followed by a polarising beam splitter (PBS). This combination gives a control over the intensity of the beam. A 50cm lens (L1) is used to focus the beam on a Type-I Bismuth Borate (BiBO) crystal of length 5 mm. The pump power before the nonlinear crystal is 5 mW. Two correlated degenerate spontaneous parametric down-converted photons are generated in the crystal in a non-collinear geometry assisted via angle tuning. The photon pairs are collimated by a 10 cm lens (L2) and separated by a prism mirror (PM) to interfere in a Mach Zehnder like setup as shown in Fig. 1. In one of the paths, a motorized translation stage MTS25-Z8, with a resolution of 29 nm, is added to compensate for the extra delay, if any. The two output ports of the beam splitter are initially used to show a HOM dip [29] as shown in Fig. 2.
Once the two polarisation entangled qubits are generated as described in the theoretical section, one can simply detect one of the qubits in the detector following path “X”. The other qubit is measured in H-V polarisation basis (path “Y” and “Z”). Measuring this other qubit in coincidence with the photon in path “X” generates random numbers as it gets detected either in the H polarisation (bit 0) or V polarisation (bit 1) at a particular instant with a 50:50 probability as shown in Fig. 1 (c) .The detectors (SPCM-800-14FC with a dark count of 100 counts per second) are identical in all three arms. To see measurement-device independence on the detector side, the diagram of the setup is slightly modified after the beam splitter to take projective measurements using quarter wave plate (QWP), HWP and a PBS combination as shown in Fig. 1 (a). On the contrary, to show the source independence, HOM curve is used as a certification technique. it’s visibility serves as a parameter for source-independence. Thus, a high visibility of the HOM curve is desired. In our case, we achieved a visibility of 97%. Since no phase information is required to generate bit streams, random bit-streams generated from maximally mixed state of a bipartite system and single photon source are identical. The extra phase information in the entangled case helps in providing security against attacks on the source. After calibration of data points A and B (as highlighted in Fig. 2) using the HOM curve, we generate entangled states at these data points.
IV. RESULTS AND DISCUSSION
In this study, we have generated two datasets of 4.5 million (M) bit streams from the experimental setup shown in Fig. 1. The data is recorded for two different cases: Dataset A is recorded at the point of highest visibility of the HOM curve of Fig. 2), which represents a maximally entangled state, and Dataset B is recorded 700 nm away from dip point which degrades the quality of the above entangled quantum state. After post-processing using Toeplitz hash function, the length of random numbers is reduced from 4.5 M to 1.2 M.
The datasets are tested against NIST-STS for quality of statistical randomness, and the results are highlighted in Table I. Kolmogorov-Smirnov test (KS test) is performed on sets with
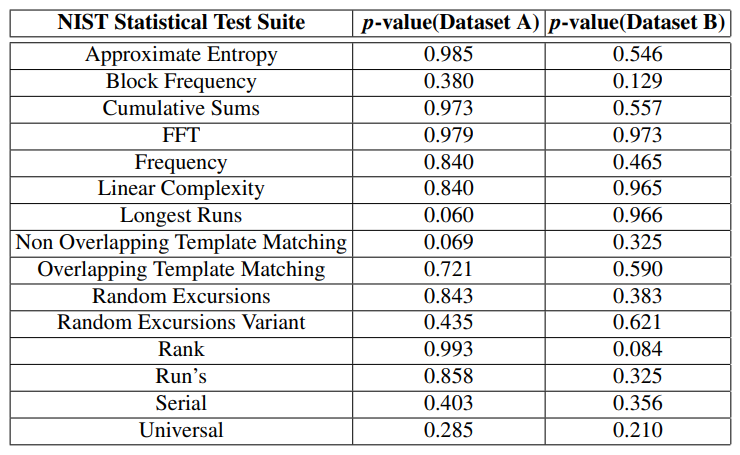
multiple p-values to provide an overall p-value indicating that they are normally distributed. Every test in Table I, shows a test-static p ≥ 0.01, suggesting that the generated dataset is statistically random.
The dataset A and B are obtained from two different quantum states, therefore having different “quantum information”. Here, we have used CHSH inequality (S) as one such quantifier of entanglement, as given in Eq. (2). The CHSH violation is measured from the direct observation as discussed in Ref. [13] and alternatively by estimating the density matrix using Bayesian and MLE quantum state tomographic techniques as in Ref.[26, 27].

The results in Table I indicate a high confidence that both the datasets have statistically independent random bit-streams. Additionally, the results shown in Table II, prove the quantum correlation. The table, although indicating quantum signature, shows some inconsistency amongst different values. This discrepancy arises due to two reasons. One that Bayesian estimation is better than MLE in cases where right prior is known (Dataset A in our case). Secondly, the effect of sampling can bias the Bayesian estimation (Dataset B in our case).
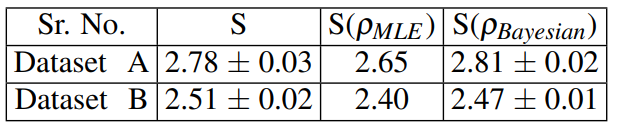
For Dataset B, right prior is not known. This requires further investigation. However, the result provided in this study positively concludes that the QRNG developed using entangled polarisation entangled photon pair is statistically random and secure against source and detector side attacks as indicated by HOM dip visibility and CHSH value respectively. A contrasting difference between our technique and randomness expansion protocols is that we have performed sequential measurements bunched together for a quantum correlation quantifier, while the semi-device independent protocols sparse them in generation and test rounds with some bias picked from a quantum source.
One open problem with random numbers is to investigate whether unpredictability and statistical properties are interrelated. To address this query, we performed scrambling operations at different lengths. One can use a quantifier from information theory, specifically min-entropy [30], defined as:

V. CONCLUSION
In this article, we have provided a sanity check of the quantum source (HOM dip) and investigated the working of a fully device-independent quantum random number generator. One can put a constraint on resources and translate the fully deviceindependent scheme to measurement device-independent or source-independent quantum random number generator protocols with automation of HWPs and calculation of smooth conditional min-entropy (based on density matrix). Other quantifiers like entanglement measure/witness can be used to define new protocols in semi-device independent regime or for higher dimensions. Also, it is theoretically proven that the visibility of the HOM curve is equal to the purity of input photons [31]. This provides a correlation between closeness to the dip point and the amount of CHSH Bell violation as indicated by Table II. Physically, it means that relative phase information between two photons is used to prove device independence and thus, preventing attacks on QRNGs from Eve. Here device independence checks can be relaxed to cases where HOM serves as a check for source independence or CHSH Bell parameter serves as a security check for measurement device independence. Sending the qubit which is being traced out here, to another party, post-processing to consider loss over the channel and together with the addition of local operations using classical communication (LOCC) can convert this random number generation scheme to device-independent quantum key distribution scheme.
[1] Claude Elwood Shannon. A mathematical theory of communication. The Bell system technical journal, 27(3):379–423, 1948.
[2] Peter Kietzmann, Thomas C Schmidt, and Matthias Wahlisch. ¨ A guideline on pseudorandom number generation (prng) in the iot. ACM Computing Surveys (CSUR), 54(6):1–38, 2021.
[3] Lih-Yuan Deng and Dale Bowman. Developments in pseudorandom number generators. Wiley Interdisciplinary Reviews: Computational Statistics, 9(5):e1404, 2017.
[4] Thomas Jennewein, Ulrich Achleitner, Gregor Weihs, Harald Weinfurter, and Anton Zeilinger. A fast and compact quantum random number generator. Review of Scientific Instruments, 71(4):1675–1680, 2000.
[5] Yi Jian, Min Ren, E Wu, Guang Wu, and Heping Zeng. Two-bit quantum random number generator based on photon-numberresolving detection. Review of Scientific Instruments, 82(7), 2011.
[6] Yong Shen, Liang Tian, and Hongxin Zou. Practical quantum random number generator based on measuring the shot noise of vacuum states. Physical Review A, 81(6):063814, 2010.
[7] Gene Novark and Emery D Berger. Dieharder: securing the heap. In Proceedings of the 17th ACM conference on Computer and communications security, pages 573–584, 2010.
[8] John Walker. Ent: a pseudorandom number sequence test program. Software and documentation available at/www. fourmilab. ch/random/S, 2008.
[9] Lawrence E Bassham III, Andrew L Rukhin, Juan Soto, James R Nechvatal, Miles E Smid, Elaine B Barker, Stefan D Leigh, Mark Levenson, Mark Vangel, David L Banks, et al. SP 800-22 rev. 1a. a statistical test suite for random and pseudorandom number generators for cryptographic applications. National Institute of Standards & Technology, 2010.
[10] Meltem Sonmez Turan, Elaine Barker, John Kelsey, K McKay, M Baish, and Mike Boyle. Nist, sp 800–90b: Recommendation for the entropy sources used for random bit generation. Tech. Rep, 2018.
[11] Barbara M. Terhal. Bell inequalities and the separability criterion. Physics Letters A, 271(5):319–326, 2000.
[12] Sonia Mazzucchi, Nicolo Leone, Stefano Azzini, Lorenzo ` Pavesi, and Valter Moretti. Entropy certification of a realistic quantum random-number generator based on single-particle entanglement. Phys. Rev. A, 104:022416, Aug 2021.
[13] Dietrich Dehlinger and MW Mitchell. Entangled photons, nonlocality, and bell inequalities in the undergraduate laboratory. American Journal of Physics, 70(9):903–910, 2002.
[14] Rutvij Bhavsar, Sammy Ragy, and Roger Colbeck. Improved device-independent randomness expansion rates using two sided randomness. New Journal of Physics, 25(9):093035, 2023.
[15] Urmila Mahadev, Umesh Vazirani, and Thomas Vidick. Efficient certifiable randomness from a single quantum device. 2022.
[16] Christopher C Gerry and Peter L Knight. Introductory quantum optics. Cambridge university press, 2023.
[17] Michael A. Nielsen and Isaac L. Chuang. Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge University Press, 2010.
[18] Xiongfeng Ma, Feihu Xu, He Xu, Xiaoqing Tan, Bing Qi, and Hoi-Kwong Lo. Postprocessing for quantum randomnumber generators: Entropy evaluation and randomness extraction. Physical Review A, 87(6):062327, 2013.
[19] William K. Wootters and W. S. Leng. Quantum entanglement as a quantifiable resource [and discussion]. Philosophical Transactions: Mathematical, Physical and Engineering Sciences, 356(1743):1717–1731, 1998.
[20] Michał Horodecki, Paweł Horodecki, and Ryszard Horodecki. Separability of mixed states: necessary and sufficient conditions. Physics Letters A, 223(1):1–8, 1996.
[21] Pawel Horodecki. Separability criterion and inseparable mixed states with positive partial transposition. Physics Letters A, 232(5):333–339, 1997.
[22] M. Lewenstein, B. Kraus, J. I. Cirac, and P. Horodecki. Optimization of entanglement witnesses. Phys. Rev. A, 62:052310, Oct 2000.
[23] John F. Clauser, Michael A. Horne, Abner Shimony, and Richard A. Holt. Proposed experiment to test local hiddenvariable theories. Phys. Rev. Lett., 23:880–884, Oct 1969.
[24] Roman Schmied. Quantum state tomography of a single qubit: comparison of methods. Journal of Modern Optics, 63(18):1744–1758, 2016.
[25] Beth Schaefer, Edward Collett, Robert Smyth, Daniel Barrett, and Beth Fraher. Measuring the stokes polarization parameters. American Journal of Physics, 75(2):163–168, 2007.
[26] Daniel F. V. James, Paul G. Kwiat, William J. Munro, and Andrew G. White. Measurement of qubits. Phys. Rev. A, 64:052312, Oct 2001.
[27] Joseph M Lukens, Kody J H Law, Ajay Jasra, and Pavel Lougovski. A practical and efficient approach for bayesian quantum state estimation. New Journal of Physics, 22(6):063038, jun 2020.
[28] Ryszard Horodecki, Pawel Horodecki, and Michal Horodecki. Violating bell inequality by mixed spin-12 states: necessary and sufficient condition. Physics Letters A, 200(5):340–344, 1995.
[29] C. K. Hong, Z. Y. Ou, and L. Mandel. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett., 59:2044–2046, Nov 1987.
[30] Robert Konig, Renato Renner, and Christian Schaffner. The operational meaning of min-and max-entropy. IEEE Transactions on Information theory, 55(9):4337–4347, 2009.
[31] Agata M Branczyk. Hong-ou-mandel interference. ´ arXiv preprint arXiv:1711.00080, 2017.
:::info
Authors:
(1) Vardaan Mongia, Quantum Science and Technology Laboratory, Physical Research Laboratory, Ahmedabad, 380009, India and Dept. of Physics, Indian Institute of Technology Gandhinagar, Gujarat, 382355, India;
(2) Abhishek Kumar, Space Weather Laboratory, Physical Research Laboratory, Ahmedabad, 380009, India;
(3) Shashi Prabhakar, Quantum Science and Technology Laboratory, Physical Research Laboratory, Ahmedabad, 380009, India;
(4) Anindya Banerji, Center for Quantum Technologies, National University of Singapore, Singapore 117543;
(5) R.P. Singh, Quantum Science and Technology Laboratory, Physical Research Laboratory, Ahmedabad, 380009, India.
:::
:::info
This paper is available on arxiv under CC BY 4.0 DEED license.
:::