Table of Links
Abstract and 1. Introduction
1.1 Related Work
-
Preliminaries
2.1 System Model
2.2 Selfish Mining Objective
2.3 Markov Decision Processes
-
Selfish Mining Attack
3.1 Overview
3.2 Formal Model
3.3 Formal Analysis
3.4 Key Features and Limitations
-
Experimental Evaluation
-
Conclusion, Acknowledgments, and References
A. NAS Mining Objectives
B. Efficient Proof Systems
C. Proof of Theorem 3.1
3.4 Key Features and Limitations
Key features. The key features of our selfish mining attack and formal analysis are as follows:
(1) Fully automated analysis. Manual (i.e. non-automated) analysis of optimal selfish mining attacks is already challenging and technically involved for PoW blockchains, where the adversary only grows a single private fork [11]. Hence, it would be even more difficult and potentially intractable in blockchains based on efficient proof systems. By modelling our selfish mining attack as an MDP and reducing the analysis to solving mean-payoff MDPs, we leverage existing methods for formal analysis of MDPs to obtain a fully automated analysis procedure, thus avoiding the necessity for tedious manual analyses.
(2) Formal guarantees on correctness. Our analysis provides formal guarantees on the correctness of its output. Again, this is achieved by formally reducing our problem to solving mean-payoff MDPs for which exact algorithms with formal correctness guarantees are available [18, 20].
(3) Flexibility of the analysis. Our analysis is agnostic to the values of system model and attack parameters and it is flexible to their changes. Hence, it allows us to tweak the parameter values and study their impact on the optimal expected relative revenue, while preserving formal guarantees on the correctness. To illustrate the flexibility, observe that:
• If the attack depth 𝑑, forking number 𝑓 or maximal fork length 𝑙 of the attack change, then both the state space and the action space of the MDP change.
• If the relative resource of the adversary 𝑝 or the switching probability 𝛾 change, then the transition function of the MDP changes.
• As we show in our experiments in Section 4, a change in any of these parameter values results in a change in the optimal expected relative revenue that the adversary can achieve.
The flexibility of our analysis is thus a significant feature, since it again avoids the need for tedious manual analyses for different parameter values that give rise to different MDPs.
Limitations. While our formal analysis computes an optimal selfish mining strategy in the MDP up to a desired precision, note that there still exist selfish mining attacks that do not correspond to any strategy in our MDP model. Hence, the strategy computed by our method is optimal only with respect to the subclass of strategies captured by the MDP model. There are two key reasons behind the incompleteness of our MDP model:
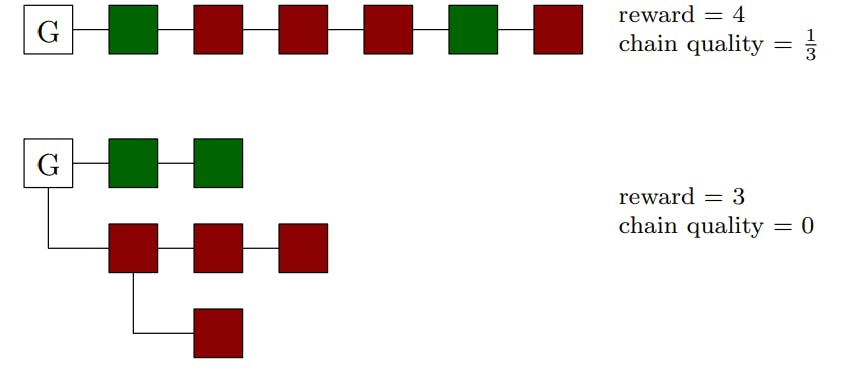
(1) Bounded forks. In order to ensure finiteness of our MDP model, we impose an upper bound 𝑙 on the maximal length of each private fork. This means that the adversary cannot grow arbitrarily long private forks. Since the probability of the adversary being able to grow extremely long private forks is low, we believe that this limitation does not significantly impact the expected relative revenue of selfish mining strategy under this restriction.
(2) Disjoint forks vs fork trees. Our attack grows private forks on different blocks in the main chain. However, rather than growing multiple disjoint private forks, a more general class of selfish mining attacks would be to allow growing private trees. We stick to disjoint private forks in order to preserve computational efficiency of our analysis, since allowing the adversary to grow private trees would result in our MDP states needing to store information about each private tree topology, which would lead to a huge blow-up in the size of the MDP. In contrast, storing disjoint private forks only requires storing fork lengths, resulting in smaller MDP models.
We conclude by noting that, while our formal analysis is incomplete due to considering a subclass of selfish mining attacks, the formal guarantees provided by our analysis still ensure that we compute a true lower bound on the expected relative revenue that a selfish mining attack achieves.
Authors:
(1) Krishnendu Chatterjee, IST Austria, Austria ([email protected]);
(2) Amirali Ebrahimzadeh, Sharif University of Technology, Iran ([email protected]);
(3) Mehrdad Karrabi, IST Austria, Austria ([email protected]);
(4) Krzysztof Pietrzak, IST Austria, Austria ([email protected]);
(5) Michelle Yeo, National University of Singapore, Singapore ([email protected]);
(6) Ðorđe Žikelić, Singapore Management University, Singapore ([email protected]).