Table of Links
Abstract and 1. Introduction
1.1 Our Approach
1.2 Our Results & Roadmap
1.3 Related Work
-
Model and Warmup and 2.1 Blockchain Model
2.2 The Miner
2.3 Game Model
2.4 Warm Up: The Greedy Allocation Function
-
The Deterministic Case and 3.1 Deterministic Upper Bound
3.2 The Immediacy-Biased Class Of Allocation Function
-
The Randomized Case
-
Discussion and References
- A. Missing Proofs for Sections 2, 3
- B. Missing Proofs for Section 4
- C. Glossary
3 The Deterministic Case
In this section, we focus on the discount model with miner ratio α ̸= 0 and some discount rate λ. Missing proofs are given in Appendix A.
3.1 Deterministic Upper Bound




By combining Eqs. (5) and (6), the proof is concluded:
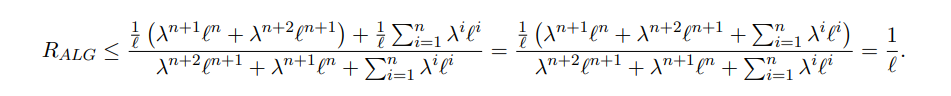
3.2 The Immediacy-Biased Class Of Allocation Function
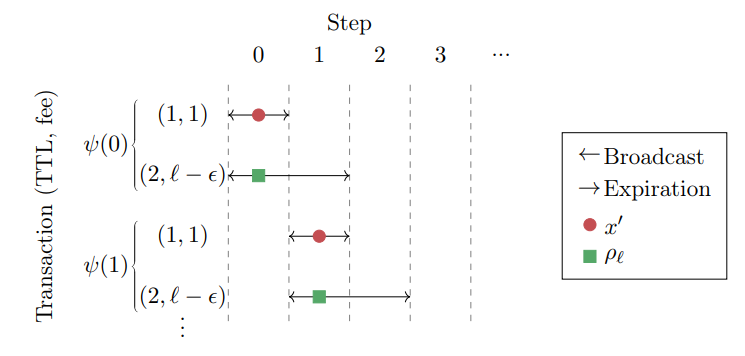
We proceed by introducing the immediacy-biased ratio class of allocation functions, and identify a regime of discount rates λ which we call the “semi-myopic” regime where it achieves the optimal deterministic competitive ratio. Given a parameter ℓ ∈ R, we denote the corresponding instance of this class as ρℓ and define it in the following manner
Definition 3.3 (The ℓ-immediacy-biased ratio allocation function ρℓ). For a set S, let

Before providing the lower and upper bound analysis, we comment on how our algorithm stands in comparison with another algorithm, MG [LSS05]. While the ℓ-immediacy-biased considers only the highest T T L = 1 transaction as a possible candidate to be scheduled instead of the highest-fee transaction, MG considers any earliest-deadline transaction. I.e., the algorithms differ in their behavior when no T T L = 1 transactions are available. However, in terms of competitive analysis, ℓ-immediacy-biased dominates ℓ-MG. That is because at any case that the ℓ-immediacy-biased allocation chooses a T T L = 1 transaction, ℓ-MG would do the same. But any case that ℓ-immediacy-biased allocation chooses the highest-fee transaction; we can force ℓ-MG to do the same by adding a (1, ϵ) with small enough ϵ to the adversary’s schedule at that step. Therefore, we can force ℓ-MG to make the same choices as ℓ-immediacy-biased allocation, without changing the optimal allocation performance.
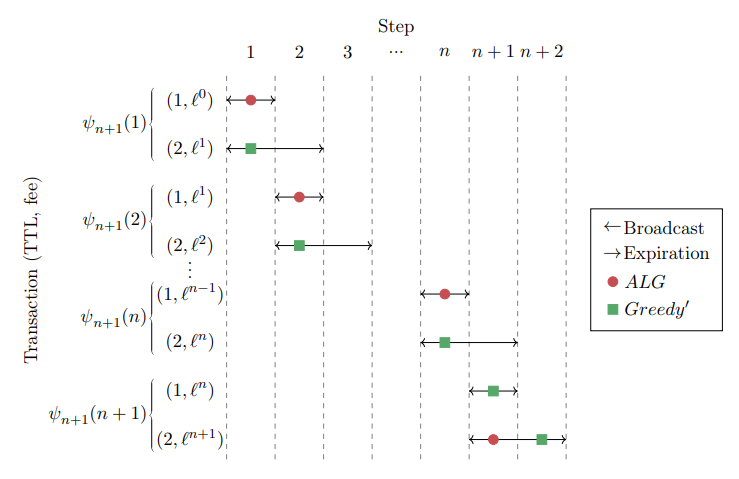
We bound the allocation function’s competitive ratio from below in Lemma 3.4.

4 The Randomized Case
Next, Theorem 4.1 obtains an upper bound on the competitive ratio of any allocation function.
4.1 Randomized Upper Bound
Theorem 4.1. Given α ̸= 0, for any (possibly randomized) allocation function ALG:
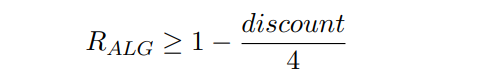
Similarly to the deterministic upper bound, the proof uses a recursive construction of adversaries where the transaction fees grow exponentially. The main technical choice is how to decide the base of the exponent. We guess it by the following equation:
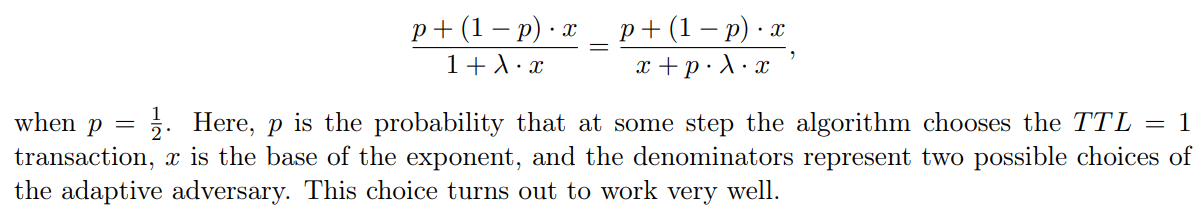
4.2 The RMIXλ Randomized Allocation Function
Next, we show that the best-known randomized allocation function known for the undiscounted case [CCFJST06], extends to the more general discount model.
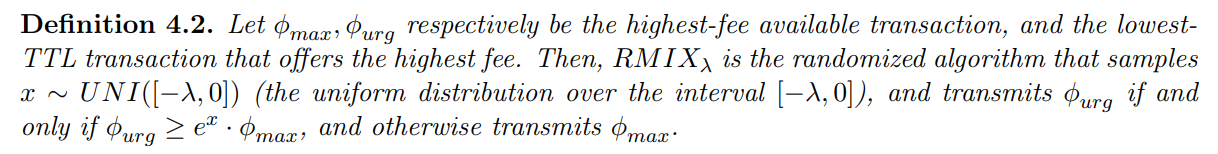
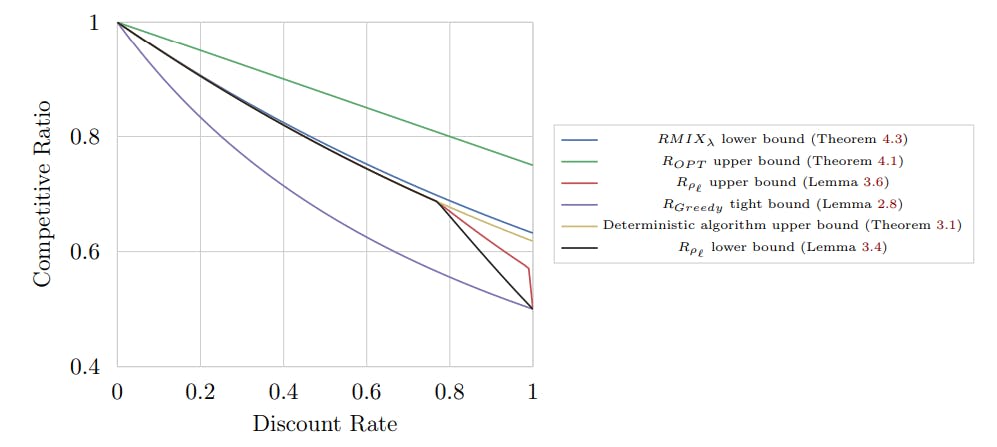
![Figure 5: Bounds for the competitive ratios of Section 3 and Section 4’s various allocation functions, for miners with a mining ratio α ̸= 0 and discount rates λ ∈ [0, 1].](https://cdn.hackernoon.com/images/fWZa4tUiBGemnqQfBGgCPf9594N2-xqb324x.png)
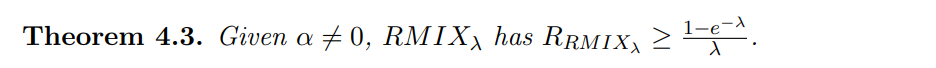
Notably, in the semi-myopic range that we identify in Section 3.2, our simple deterministic allocation achieves very similar performance to the above randomized allocation function.
Our competitive ratio results are summarized in Fig. 5.
:::info
Authors:
(1) Yotam Gafni, Weizmann Institute ([email protected]);
(2) Aviv Yaish, The Hebrew University, Jerusalem ([email protected]).
:::
:::info
This paper is available on arxiv under CC BY 4.0 DEED license.
:::